基于ABAQUS非线性接触分析的球型支座转动性能及结构分析

李冰，王少华，严情木

(1.西南交通大学新型驱动技术中心，四川成都 610031;2.西南交通大学机械工程研究所，四川成都 610031)

桥梁支座是连接桥梁上部结构和下部结构的重要结构部件。它能将桥梁上部结构的反力和变形(位移和转角)可靠地传递给桥梁下部结构，以适应梁体自由伸缩及转动的需要。目前应用广泛的桥梁支座形式有板式橡胶支座、盆式橡胶支座、球型支座等［1］。板式橡胶支座结构简单、成本低廉，但承载能力较低;盆式橡胶支座承载能力较高、滑动摩擦系数小、转动灵活，但橡胶材料易老化、设计转角较小［2-3］;球型支座设计转角可远大于盆式橡胶支座，一般为0.01～0.02 rad，必要时也可以达到0.05 rad，承载能力高，可适应于大跨度桥梁的应用。球型支座在转动力矩作用下，会在转动接触面之间发生较大位移和转动，对结构承载方式会产生显著影响，必须在分析中加以考虑。通过建立常规力学模型分析球型支座转动性能，并通过非线性接触有限元分析方法进行验证，确定球型支座的转动条件。研究不同转角下球型支座各部件应力分布情况，在此基础上，研究了球型支座主要设计参数对支座性能的影响。分析计算结果对以后球型支座的优化设计和应用有重要的理论意义和实用价值。

1 球型支座的转动分析

1.1 球型支座结构

球型支座基本结构示意如图1［4］。

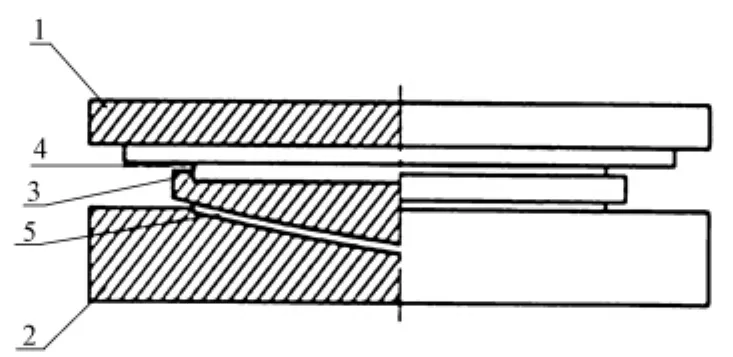
图1 球型支座基本结构示意

1.2 球型支座力学模型分析

在转动力矩作用下，球型支座在球面四氟板处发生转动［1］，建立球型支座力学模型如图2所示。图中，m为上部结构质量，P为球型支座所受的正压力，R为球面曲率半径，e为上部结构由于转动产生的重力偏心距。

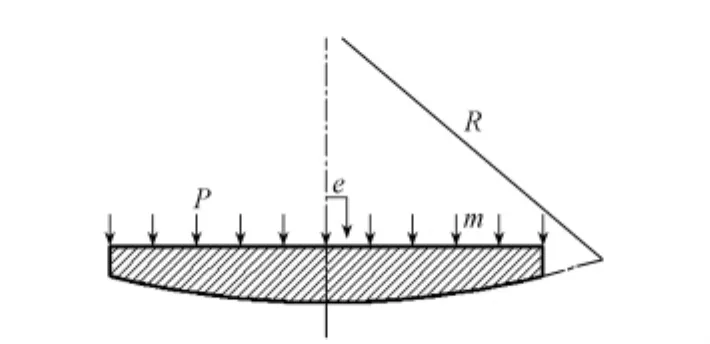
图2 球型支座转动示力图

建立该系统的平衡方程为

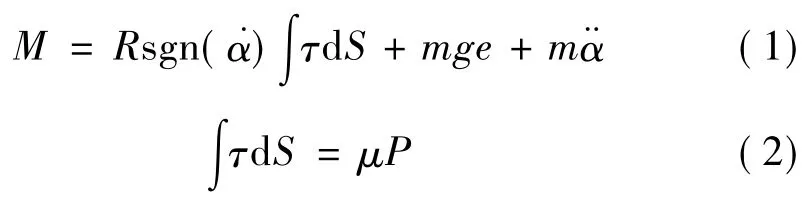
式中，M为施加的转动力矩，τ为球面单位面积摩擦力，μ为摩擦系数，为角速度，为角加速度，sgn为符号函数，其值为

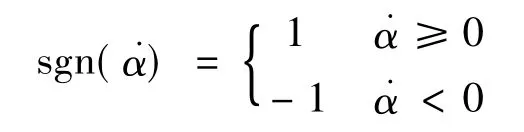
由于实际转动过程中产生的重力偏心距e相对于球面曲率半径R很小，球型支座可以视为匀速转动，因此式(1)可以简化为

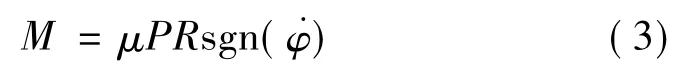
由上式可以看出，转动力矩M与正压力P、摩擦系数μ、球面半径R近似成正比例关系，球型支座一旦克服摩擦就可以发生转动，此时转角的大小与转动力矩几乎无关，因此球型支座可以适应各种转角的需要，同时为了防止出现过大的转角而使结构安全得不到保证，需要安装限位装置。

1.3 球型支座有限元模型

由于球型支座结构的对称性，建立球型支座的1/2实体模型进行有限元建模和计算。接触类型选择有限滑动，这种接触类型允许接触面之间出现任何大小的相对滑动和转动，适用于大位移非线性接触分析。在为接触分析选择单元类型时，将会构成从面的模型部分选用一阶单元，使计算结果更容易收敛［5］。球型支座中铸钢结构弹性模量E=2.05×105MPa，泊松比v=0.3，聚四氟乙烯材料弹性模量E=1 500 MPa，泊松比v=0.4，混凝土结构弹性模量E=3.3×104MPa，泊松比v=0.2。

支座竖向承压，载荷大小为10 MN，为了使模型和计算结果与实际工况更加符合，需要加入桥跨结构和墩台结构，并研究桥跨结构底面积大小对球型支座受力情况的影响，设上支座板面积为S，分别取桥跨结构的底面积为S、2S、3S、4S进行计算，结果显示在桥跨结构厚度达到支座厚度3倍后［6］，底面积大小对支座各部件复合应力计算结果影响较小，为了提高计算效率，取桥跨结构底面积大小与上支座板面积相等，建立球型支座1/2实体模型。

1.4 非线性接触分析

以有限元模型为基础，研究球型支座正压力P、摩擦系数μ、球面曲率半径R、转角α等对转动力矩的影响。有限元分析结果与理论分析结果M=μPR一致，转动力矩与球面半径R近似成正比例关系，有限元计算结果与理论值相差1.3%，见图3。转动力矩与转角大小几乎无关，转角为0.01～0.04 rad时，转动力矩为不变值47 kN·m。由此可知，采用大位移非线性有限元分析方法对球型支座转动性能及结构进行分析是正确合理的。

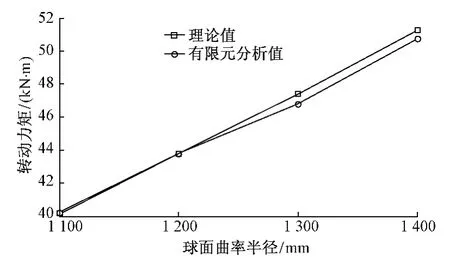
图3 球面曲率半径与转动力矩关系

2 球型支座转动时的应力分析

2.1 无转动时的应力分析结果

在设计载荷作用下，铸钢结构最大复合应力远低于材料的许用应力，最大应力出现在上盖板处，不会对结构造成破坏。平面四氟板和球面四氟板的复合应力符合聚四氟乙烯材料的许用应力，分布规律为中间应力较小，呈环形往外扩展，应力逐渐增大，最大应力发生在四氟板的边缘处［6］。

2.2 转动时的应力分析结果

如图4为0.02 rad转角下球型支座复合应力云图，图5为0.02 rad转角下球冠衬板复合应力云图，图6为无转动时球面四氟板复合应力云图，图7为0.02 rad转角下球面四氟板复合应力云图，图8，图9分别为不同转角下铸钢结构和四氟板最大复合应力值。

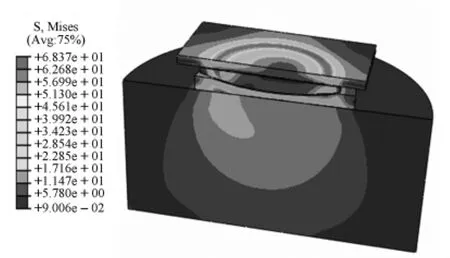
图4 0.02 rad转角下球型支座复合应力云图

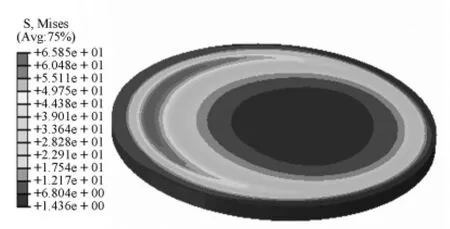
图5 0.02 rad转角下球冠衬板复合应力云图

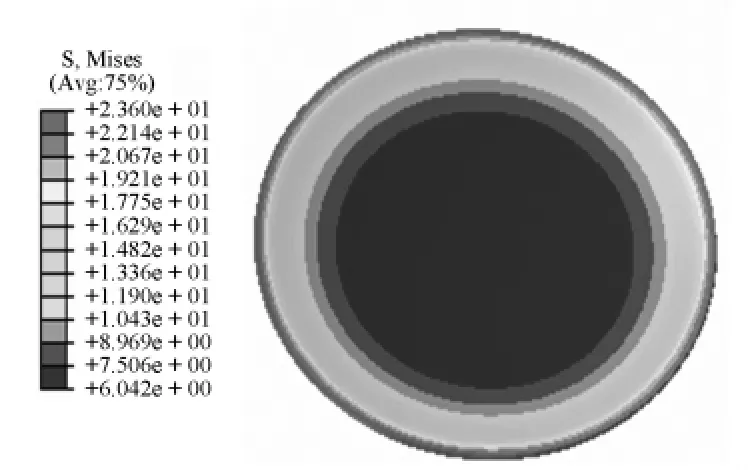
图6 无转动时球面四氟板复合应力云图

图7 0.02 rad转角下球面四氟板复合应力云图

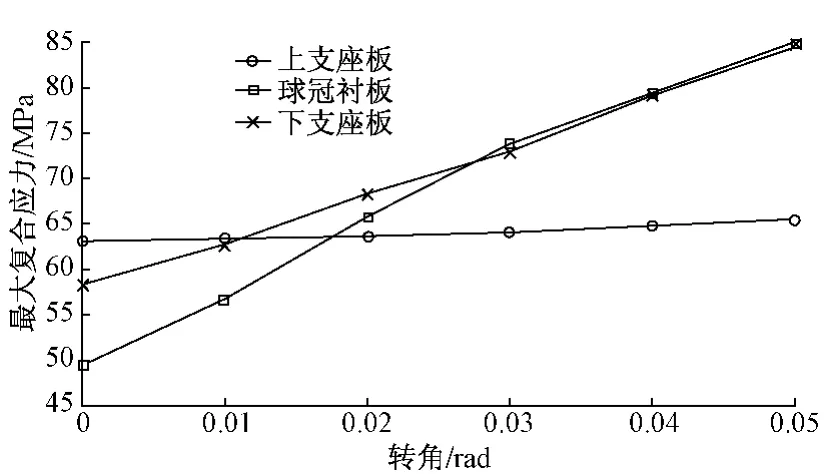
图8 不同转角下铸钢结构最大复合应力值

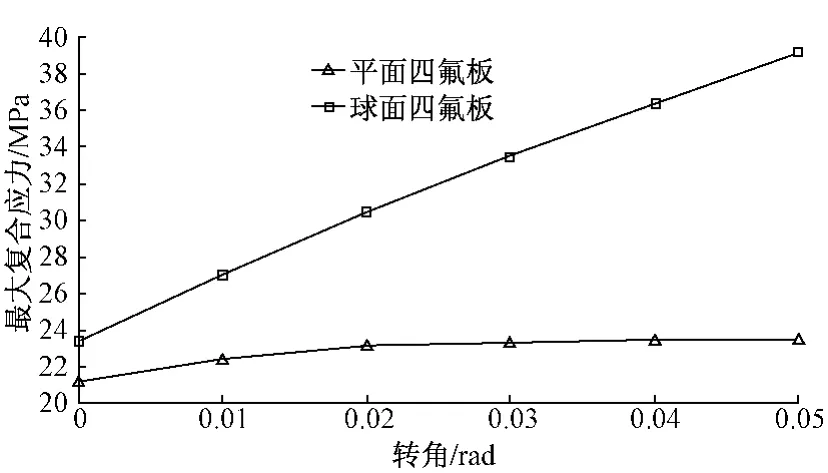
图9 不同转角下四氟板最大复合应力值

由图4和图5可以看出，当转角为0.02 rad时，球冠衬板一侧端部靠里部分产生了较大复合应力，这是由于支座转动时该侧球冠衬板与球面四氟板接触面积减小，发生了较大的下挠导致了较大的拉应力。

由图6和图7可以看出，当球型支座发生0.02 rad转动时，球面四氟板最大复合应力值增加了30%，中心处复合应力值变化较小，最大复合应力发生在球面四氟板的一侧边缘处。

由图8可以看出，随着转角的增大，球冠衬板、下支座板最大复合应力有较大增加，上支座板最大复合应力变化较小，但都远小于铸钢材料的许用应力，因此发生转动时铸钢结构的可靠性较高。

由图9可以看出，随着转角的增大，平面四氟板和球面四氟板的最大复合应力均增加，但球面四氟板最大应力增加值远大于平面四氟板，当转角达到0.02 rad时，球面四氟板的最大复合应力为30.47 MPa，大于聚四氟乙烯材料的许用应力30.00 MPa。因此设计中应考虑转动工况下球型支座的应力值，以防止支座可靠性的降低，保证支座的安全。

3 球型支座结构参数变化对支座性能的影响

由上述分析可知，随着转角的增大，球型支座各部件应力值均增加，尤其是球面四氟板应力值超出了许用应力，因此对转动工况下的球型支座进行设计优化具有重要的意义。为充分研究结构参数变化对支座性能的影响，利用非线性接触分析分别计算了球型支座在0.02 rad转角下，球面四氟板厚度、球冠衬板厚度、球面曲率半径对支座各部件最大复合应力值的影响。如图10为球面四氟板厚度对球面四氟板最大复合应力的影响，图11为球面曲率半径对四氟板最大复合应力的影响。

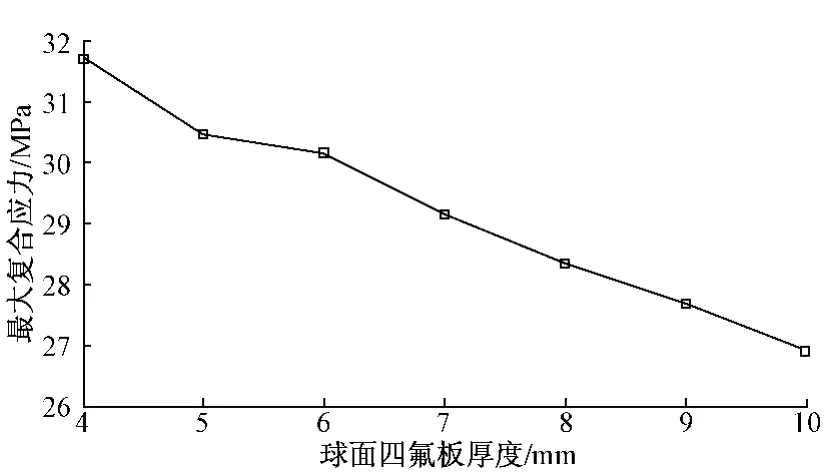
图10 不同球面四氟板厚度下球面四氟板最大应力值

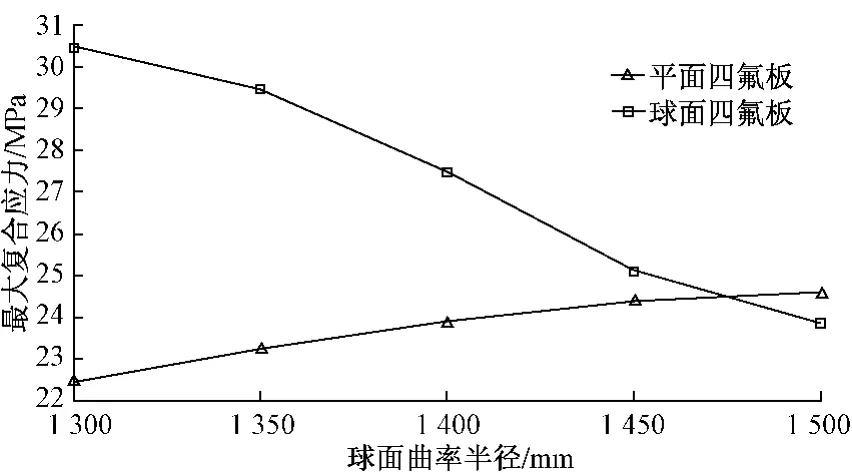
图11 不同球面曲率半径下四氟板最大应力值

分析结果表明，球面四氟板厚度对球面四氟板最大复合应力值影响较大，对其他部件影响较小，由图10可以看出，随着厚度的增加球面四氟板最大应力值降低了15.2%，在考虑结构设计要求及成本的前提下，应尽量增大球面四氟板厚度。球冠衬板厚度对支座各部件最大复合应力值影响较小，在满足结构设计要求前提下，应尽量减小球冠衬板厚度，降低成本。球面曲率半径对支座最大复合应力影响较大，下支座板、球冠衬板最大复合应力有明显降低。

由图11可以看出，随着球面曲率半径的增大，平面四氟板最大复合应力增加了9.3%，但仍小于许用应力，球面四氟板最大复合应力值降低了21.6%，平面四氟板和球面四氟板最大复合应力值逐渐接近，便于采用等强度设计法对四氟板进行结构设计，但过大的球面曲率半径下，球型支座转动过程中位移量太大，使安全性减低，因此在结构设计合理的前提下，应尽量增大球面曲率半径。

4 结论

1)采用ABAQUS非线性接触分析对球型支座转动力矩进行验证，分析结果与理论计算一致，有M=μPR，说明采用非线性接触分析对球型支座进行研究是合理的。

2)转动情况下，球型支座各部件应力较无转动工况下有明显增加，应力值随转角的增大而增加，且球面四氟板最大复合应力超过了许用应力，为保证球型支座使用安全，设计中必须考虑转动工况。

3)在满足结构设计要求的前提下，增大球面四氟板厚度和球面曲率半径，可以降低转动工况下球面四氟板最大复合应力值，使球型支座各部件应力均低于许用应力，改善支座的性能。

［1］ 庄军生．桥梁支座［M］．北京:中国铁道出版社，2000．

［2］ 刘岳兵，王少华，王宏谋，等．盆式橡胶支座结构及混凝土墩台非线性有限元分析［J］．铁道建筑，2010(9):28-30．

［3］ 刘岳兵，王少华，王宏谋，等．基于ANSYS分析的盆式橡胶支座结构及性能研究［J］．铁道建筑，2009(10):1-3．

［4］ 中华人民共和国国家标准．GB/T 17955—2009 桥梁球型支座［S］．北京:国家标准管理委员会，2009．

［5］ 庄茁．基于ABAQUS的有限元分析和应用［M］．北京:清华大学出版社，2008．

［6］ 何维．桥梁支座结构分析及疲劳性能研究［D］．成都:西南交通大学，2011．