中强度预应力HR钢棒在混凝土中的锚固试验及可靠度分析
陈 萌,毕苏萍,王宝朝,刘立新
(郑州大学 土木工程学院,河南 郑州 450002)
预应力HR钢棒(helical ribbed bar,代号HR)即预应力螺旋肋钢棒,是一种沿着表面纵向,具有规则间隔连续螺旋肋的钢棒,其等强度的极限强度标准值变化范围为800~1 270 N/mm2。螺旋肋钢棒具有延性好、低松弛性、与混凝土握裹力强和良好的可焊接性等优点,在国外已被广泛应用在高速铁路预应力混凝土轨枕板、预应力混凝土输水管道、预应力混凝土电线杆和预应力混凝土空心楼板等构件中。为了加快中强度预应力螺旋肋钢棒在国内的推广应用,本文对其在混凝土中的黏结锚固性能展开深入的试验研究,并通过可靠度分析,提出预应力螺旋肋钢棒在混凝土中锚固长度计算方法的建议公式[1-2]。
1 试验方案
1.1 HR钢棒的基本力学性能
试验用螺旋肋钢棒公称直径分别为7 mm和9 mm,每种直径的钢棒对应两种不同的强度类别,即A类(抗拉强度标准值800 MPa)和B类(抗拉强度标准值900 MPa),HR钢棒的材料性能试验结果见表1。
1.2 构件设计
考虑混凝土强度、钢棒直径、锚固长度、保护层厚度和劈裂面配箍率等主要黏结锚固性能因素的影响,试验共设计17组68个中强度预应力螺旋肋钢棒拉拔构件,试验方案如表2所示。

表1 预应力HR钢棒的材料力学性能试验结果
在WE-30型液压式万能试验机上进行锚固试验,根据《混凝土结构试验方法标准》(GB 50152―92)的要求分级加载;试验构件加载端设计50 mm长的无黏结长度以避免局部压坏;构件所受的拉拔力由油压表记录;构件加载端设置两个百分表测定其滑移,构件自由端设置一个百分表测定其滑移,百分表连接到CM-10应变仪上用计算机记录每级的读数。
2 HR钢棒锚固影响因素分析
2.1 混凝土强度的影响
A3-Ⅰ,A3-Ⅱ和 A3-Ⅲ共3组12个拉拔构件,钢棒直径d=7 mm,锚固长度la=100 mm,保护层厚度c=46.5 mm,襞裂面配箍率ρsv=0,考虑混凝土强度的影响(混凝土抗拉强度 ft变化范围为2.41~2.90 MPa)[3]。
黏结强度与混凝土抗拉强度之间的变化关系见图1。由图1可知,预应力螺旋肋钢棒黏结强度随着混凝土抗拉强度的提高而提高,二者大致呈线性关系,由图1中试验点回归得到黏结强度与混凝土抗拉强度的关系式为

表2 预应力HR钢棒锚固试验方案

图1 混凝土强度的影响

2.2 锚固长度的影响
B3类构件(B3-Ⅰ,B3-Ⅱ,B3-Ⅲ)和 C3 类构件(C3-Ⅰ,C3-Ⅱ,C3-Ⅲ,C3-Ⅳ)共 7 组 28 个构件。构件中保护层厚度c的变化范围为45.5~46.5 mm,襞裂面配箍率ρsv=0,混凝土抗拉强度ft变化范围为2.42~2.88 MPa,钢棒直径变化范围为7~9 mm,上述条件基本相近,考虑锚固长度的影响(锚固长度la变化范围为70~270 mm)。为消除直径和混凝土强度的影响,考虑相对锚固长度la/d与相对黏结强度τu/ft二者之间的相互关系。
试验结果表明,当其他条件基本相同时,最大相对平均黏结强度τu/ft随着锚固长度la的增大而减小,这是因为当锚固长度较大时,高黏结应力区段相对较小,黏结应力沿锚固长度分布不均匀,从而导致黏结锚固强度减小。
相对黏结强度τu/ft与d/la之间大致呈线性关系,见图2,回归结果为公式(2)。

图2 锚固长度的影响

2.3 相对保护层厚度的影响
A3-Ⅰ组和 D3 类构件(D3-Ⅰ,D3-Ⅱ,D3-Ⅲ)共 4组16个构件。混凝土强度ft=2.41 MPa,钢棒直径d=7 mm,锚固长度la=100 mm,襞裂面配箍率ρsv=0,考虑相对保护层厚度的影响(相对保护层厚度c/d=2.14~6.64)。
相对黏结强度与相对保护层厚度之间的变化关系见图3。预应力螺旋肋钢棒相对黏结强度随着相对保护层厚度的提高而提高,二者大致呈线性关系,由图3中试验点回归得到相对黏结强度与相对保护层厚度的关系式式(3)。
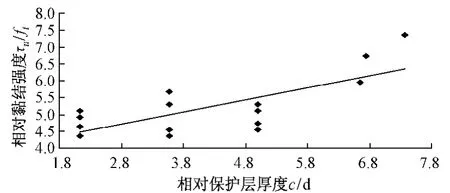
图3 相对保护层厚度的影响

2.4 襞裂面配箍率的影响
A3-Ⅰ组,D 类构件(D3-Ⅰ,D3-Ⅱ,D3-Ⅲ)和 E 类构件(E3-Ⅰ,E3-Ⅱ,E3-Ⅱ,E3-Ⅳ)共 8 组 32 个构件,混凝土抗拉强度ft=2.41 MPa,钢筋直径d=7 mm,锚固长度la=100 mm,考虑配箍率的影响(配箍率ρsv变化范围为0~2.1%)。
试验构件劈裂后箍筋起到侧向约束的作用,箍筋对延缓劈裂的作用较小,相对黏结强度与劈裂面配箍率大体呈正比关系,如图4所示。

图4 横向配箍率的影响
2.5 HR钢棒黏结锚固强度计算公式
依据试验结果,考虑混凝土强度、锚固长度、相对保护层厚度和劈裂面配箍率等锚固因素的影响,回归得到HR钢棒极限黏结强度计算公式为

对68个试验构件,经式(4)计算求得极限黏结强度试验值与计算值比值的平均值μ=1.052,变异系数δ=0.170 2。
3 可靠度分析
在锚固设计中,为了使锚固可靠度高于构件截面强度的可靠度,还需要采用附加的可靠度β0(β0=1.57),此可靠度指标是锚固设计中确定锚固长度设计值的计算依据。
由于β值在1.0~2.0之间,近似取锚固抗力R和作用效应S均服从对数正态分布,因此,采用中心点法进行锚固极限状态的可靠度分析,中心点法计算简单,且精度能够满足工程应用的要求[4]。
3.1 锚固的极限状态方程
锚固极限状态下的平衡条件为

式中,Fu为极限拉拔力;τu为极限黏结强度;lcra为临界锚固长度;d为钢棒直径。
将式(6)代入到式(5)中,得到锚固设计的极限状态方程为

令作用效应

锚固抗力R为

则式(7)即变成常用的极限状态方程

3.2 统计数据
3.2.1 钢棒屈服强度fy的平均值与变异系数
在试验资料的基础上,取A类螺旋肋钢棒屈服强度fpy的平均值 μfpy=741.2 MPa,变异系数 δfpy=0.064 1;B类螺旋肋钢棒屈服强度fpy的平均值μfpy=995.8 MPa,变异系数 δfpy=0.064 1。
3.2.2 构件混凝土抗拉强度ft的平均值与变异系数
在大量试验资料统计的基础上,得出常用的混凝土强度等级C20,C30,C40,C50和C60抗拉强度的平均值与变异系数,如表3所示[5-6]。

表3 混凝土抗拉强度的平均值与变异系数
3.2.3 几何尺寸的平均值与变异系数
表4中列出了锚固长度、保护层厚度、钢棒直径和箍筋平均间距的平均值与变异系数。

表4 构件几何尺寸的平均值与变异系数
3.2.4 计算模式准确性Ωp的统计参数
极限黏结强度试验实测值与回归计算值的比值,即为计算模式准确性系数Ωp。依据公式(4)的计算结果统计得出:准确性系数Ωp的平均值μΩp=1.052,变异系数 δΩp=0.170 2。
3.3 中心点法求解锚固长度
3.3.1 极限状态方程作用效应S的平均值与变异系数
作用效应S的平均值μs为

作用效应S的变异系数δs为

3.3.2 抗力R的平均值与变异系数

式中,Rp为按公式(4)计算求得的抗力。则抗力Rp的平均值 μRp为

抗力Rp的方差σ2Rp为

式中,Xi表示R的有关随机变量混凝土强度ft;下标m表示偏导数中的随机变量均以各自的平均值赋值[7-8]。抗力 Rp的变异系数 δRp为

将式(4)和式(9)代入式(13),得


在式(18)中,令

则M1的平均值μM1为

M1的方差为

M1的变异系数 δM1为
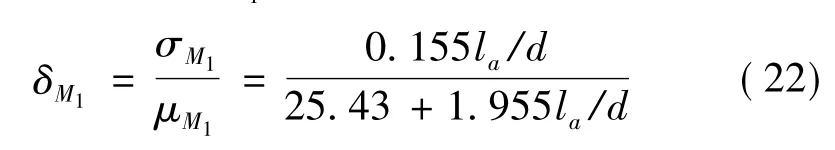
即可求得抗力R的平均值μR为

抗力R的变异系数δR为
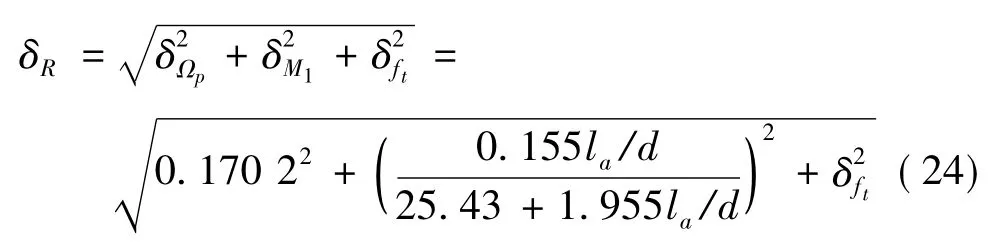
由于β0=1.57,1<β0<2且服从对数正态分布,可得β0的计算公式为

将式(11)、式(12)、式(23)和式(24)代入到式(25)中,得

将表3中不同强度等级混凝土抗拉强度的平均值与变异系数代入到式(26)中,可分别求得A类和B类螺旋肋钢棒锚固长度的近似值[9]。
基于可靠度计算及试验分析结果,为方便工程应用,本文提出螺旋肋钢棒基本锚固长度建议公式为

式中,lab为钢棒的基本锚固长度;fpy为钢棒的抗拉强度设计值;ft为混凝土轴心抗拉强度设计值,当混凝土强度等级高于C60时,按C60取值。
采用中心点法和建议公式式(27)计算的A类和B类螺旋肋钢棒锚固长度值见表5和表6。
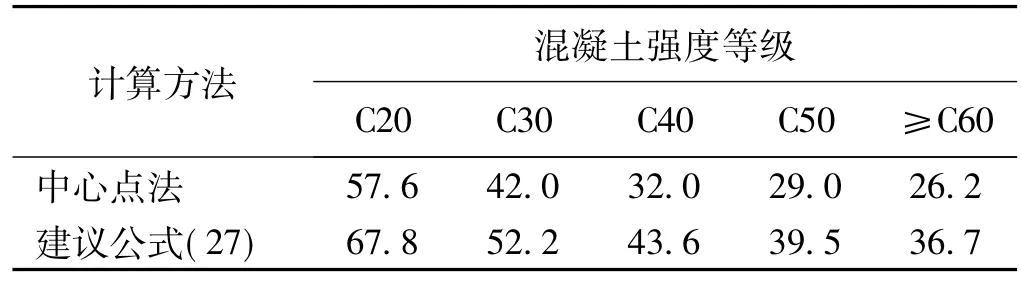
表5 A类螺旋肋钢棒锚固长度 mm

表6 B类螺旋肋钢棒锚固长度 mm
4 结论
1)通过68个螺旋肋钢棒黏结锚固构件的拉拔试验,详细分析了混凝土强度、锚固长度、相对保护层厚度和配箍率等因素对黏结锚固的影响,在试验结果的基础上,回归得到螺旋肋钢棒极限黏结锚固强度的计算公式,计算结果与试验结果吻合良好。
2)基于黏结锚固试验数据,并参考大量试验统计资料,采用中心点法进行了锚固极限状态的可靠度分析,并提出了螺旋肋钢棒在混凝土中的黏结锚固长度设计建议。
[1] 中国钢铁工业协会.GB/T 5223.3—2005 预应力混凝土用钢棒[S].北京:中国标准出版社,2005.
[2] European Committee for standardization.Eurocode 2:Design of concrete structures(BS EN 1992-1-1:2004(E))[S].Brussels:European Committee for standardization,2004.
[3] 刘立新,李殿文,陈萌.细晶粒热轧带肋钢筋黏结锚固性能试验研究[J].工业建筑,2011,41(2):61-65.
[4] 赵国藩.工程结构可靠度[M].北京:水利电力出版社,1984.
[5] 徐有邻,周氐.混凝土结构设计规范理解与应用[M].北京:中国建筑工业出版社,2002.
[6] 中华人民共和国住房和城乡建设部.GB 50010—2010 混凝土结构设计规范[S].北京:中国建筑工业出版社,2010.
[7] 邵卓民,沈文都,徐友邻.钢筋砼的锚固可靠度及锚固设计[J].建筑结构学报,1987(4):36-49.
[8] 解伟,牟晓光,李树山.螺旋槽预应力钢棒黏结锚固可靠度分析与设计建议[J].铁道建筑,2011(5):128-130.
[9] 中华人民共和国建设部.GB 50068—2001 建筑结构可靠度设计统一标准[S].北京:中国建筑工业出版社,2001.

