K30试验数据的曲线拟合分析方法

陈 辉，颜胜才，孟军涛，李晋平，胡在良

(中国铁道科学研究院铁道建筑研究所，北京 100081)

K30平板荷载试验是在直径为30 cm的平板上施加荷载，检测反映路基强度与变形参数等承载力指标的试验方法。德国、日本等国家制定了相应的平板荷载试验规程和标准。我国在大秦重载铁路建设中，开始以K30平板荷载试验检测地基系数K30值作为路基施工质量监控指标，之后在广深准高速铁路中得到应用，并在新建铁路和高速铁路上得以推广。在秦沈客运专线路基的设计和施工中，首次采用压实系数(或孔隙率)和地基系数K30值作为双控指标来评定路基施工质量，根据路基填筑部位、填料的不同，其压实标准——压实系数(或孔隙率)和地基系数K30值应满足相应的规定。因此，K30平板荷载试验已成为路基填筑质量控制的主要检测手段。

目前，K30平板荷载试验的数据处理主要采用手工绘制荷载与下沉量的关系曲线，然后从荷载与下沉量关系曲线上找出下沉量基准值对应的荷载强度，来计算地基系数K30值。这种方法计算出来的K30值具有一定的主观性，不同的人员对于同一组数据的计算结果会有所不同，甚至同一人员不同时间对同一组数据的计算结果也可能不同。因此，为保证地基系数K30值的计算结果科学准确，研究K30值的计算方法具有现实意义。

1 荷载—沉降量拟合曲线方程的假定与计算

1.1 方程的假定

将试验测出的若干组荷载和下沉量数据，采用二次多项式拟合，假设荷载—下沉量二次曲线方程为

式中，σ为荷载板下的应力，MPa;S为荷载板中心的下沉量，mm;a1和a2为系数。

该曲线方程的顶点式可写为

其顶点坐标为(-0.5a1/a2，-0.25/a2)。

以上拟合方法基于两点假设：①该曲线方程必须经过原点且a2＞0，所以假设该方程没有常数项;②假设原点之后(理解为σ＞0)的曲线没有负值S出现为正常曲线，反之为异常曲线。当σ1=-0.5a1/a2≤0，即a1≥0时，为正常曲线;当σ2=-0.5a1/a2＞0，即a1＜0时，原点之后有一段负值S出现，所以为异常曲线。对于异常曲线，建议把所计算出来的地基系数K30值作为参考值，因为这样拟合出来的曲线也比较好。

如图1所示，曲线1(-0.5a1/a2＜0)和曲线2(-0.5a1/a2=0)为正常曲线;曲线3(-0.5a1/a2＞0)为异常曲线。

图1 正常曲线和异常曲线示意(a2＞0)

当a2=0且a1≠0时，曲线方程变为S=a1σ，即为一条通过原点的直线方程，属于直线拟合，当a1＞0时，直线为通过原点的正比直线，为正常曲线;当a1＜0时，直线为通过原点的反比直线，为异常曲线。

当a2＜0时，不符合地基系数K30检测试验规律，在此不作讨论。

1.2 方程系数的计算

根据实测值确定关系式(1)，实际上就是确定(1)式中的系数a1和a2。系数a1和a2的确定要符合该系数能使曲线对各级实测值的偏差最小的原则。

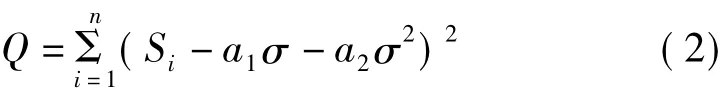
即：

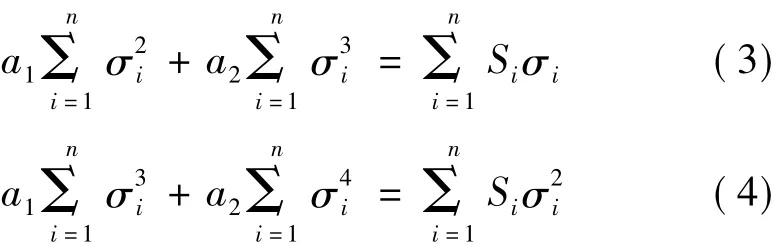
由式(3)和式(4)可求出系数a1和a2。

1.3 地基系数K30试验结果的计算

根据每级试验数据绘出荷载强度与下沉量关系曲线，从曲线上找出下沉量基准值对应的荷载强度，并按下式计算地基系数K30值。

式中，K30为由直径30 cm的荷载板测得的地基系数，MPa/m;σs为荷载强度与下沉量关系曲线上下沉量为1.25mm对应的荷载强度，MPa;Ss为下沉量基准值，为1.25mm。

2 应用实例与分析

2.1 正常曲线拟合实例

第一组铁路路基检测下沉量数据：0.10mm，0.21 mm，0.45mm，0.73 mm，1.00mm。所对应的荷载值分别为：40 kPa，80 kPa，120 kPa，160 kPa，200 kPa。用上述方法拟合求得的方程系数a1=0.001 6，a2=1.729 4×10-5，-a1/(2a2)=-46.84，地基系数 K30值是226.1/1.25=180.9 MPa/m。其拟合曲线如图2所示。

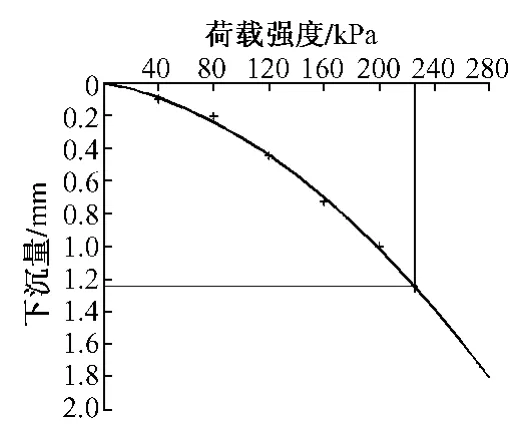
图2 正常拟合曲线(读数：226.1 kPa，1.25mm)

2.2 不正常曲线拟合实例

第二组铁路路基检测下沉量数据：0.03 mm，0.11 mm，0.25mm，0.83 mm，1.10mm。所对应的荷载值分别为：40 kPa，80 kPa，120 kPa，160 kPa，200 kPa。用上述方法拟合求得的方程系数 a1=-0.001 3，a2=3.552 0 ×10-5，-0.5a1/a2=18.99，地基系数 K30参考值是207.5/1.25=166 MPa/m。其拟合曲线如图3所示。

图3 异常拟合曲线(读数：207.5 kPa，1.25mm)

2.3 直线拟合实例

第三组铁路路基检测下沉量数据：0.2 mm，0.38 mm，0.58 mm，0.77 mm，1.02 mm。所对应的荷载值分别为：40 kPa，80 kPa，120 kPa，160 kPa，200 kPa。用上述直线方法拟合求得的方程系数a1=0.004 9，a2=0，地基系数K30值是252.8/1.25=202.2 MPa/m。其拟合直线如图4所示。

图4 直线拟合(读数：252.8 kPa，1.25mm)

2.4 曲线拟合和直线拟合对比评价

下面用均方误差来评价拟合数据准确性、可靠性，均方误差定义为各拟合值与实测值误差的平方和的平均值的平方根，又称为标准误差。

设 n 个拟合值与实测值的误差为 ε1，ε2，…，εn，则这组拟合值与实测值的均方误差δ为

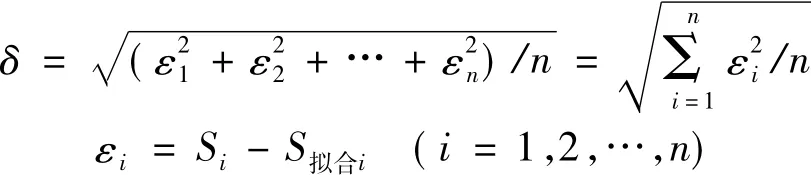
式中，Si是实测的下沉量，S拟合i是拟合后对应的下沉量。

需要注意的是，均方误差只是对一组实测数据拟合值准确性、可靠性的估计。均方误差越小，拟合值的准确性、可靠性越大一些，反之，拟合值就不大准确、可靠。

为显示可比性，必须对同一组数据进行拟合。对第一组数据进行线性拟合，拟合直线如图5所示。经过计算，地基系数K30为280.9/1.25=224.7 MPa/m，曲线拟合时的均方误差为0.020 3 mm，直线拟合时的均方误差为0.096 8 mm。

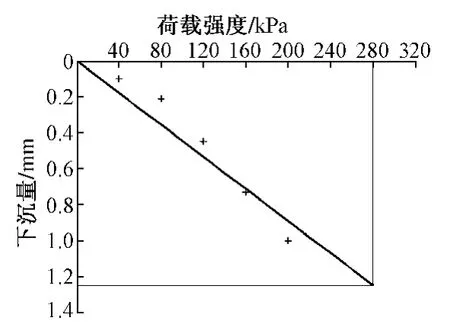
图5 直线拟合(读数：280.9 kPa，1.25mm)

对第三组数据进行曲线拟合，拟合曲线如图6所示，地基系数 K30值是242.4/1.25=193.9 MPa/m。经过计算，曲线拟合时的均方误差为0.012 4 mm，直线拟合时的均方误差为0.019 2 mm。

图6 正常拟合曲线(读数：242.4 kPa，1.25mm)

比较可知，曲线拟合时的均方误差比较小，拟合得较好。对于接近线性的实测K30试验数据来说，直线拟合时的均方误差与曲线拟合时的均方误差差别不大，两种方法都可以选用;对于非线性的实测K30试验数据，直线拟合时的均方误差与曲线拟合时的均方误差差别较大，宜选用曲线拟合计算。与直线拟合对比，曲线拟合误差小，计算结果更准确可靠，对实测数据计算的地基系数K30偏小，曲线拟合评价结果偏于严格，能更好地控制路基工程质量。

3 结语

二次多项式曲线拟合法可用于对地基系数K30试验数据的处理，通过拟合得出的地基系数K30值误差较小。

通过工程实例分析了曲线拟合和直线拟合的准确性和可靠性。对于接近线性的实测K30试验数据来说，曲线拟合法和直线拟合法都可以选用;对于非线性的实测K30试验数据，宜选用曲线拟合计算。

实际检测应用验证了该方法的准确性与可靠性，在铁路路基工程中检测地基系数指标时可以参考应用。

［1］中华人民共和国铁道部.TB 10102—2010 铁路工程土工试验规程［S］.北京：中国铁道出版社，2010.

［2］龙卫，肖金凤.变形模量Ev2与K30平板载荷试验的对比分析［J］.铁道建筑技术，2006(5)：36-39.

［3］梁波，王志刚，丁立.粉煤灰基床或路堤填料的K30试验［J］.路基工程，2000(1)：17-21.

［4］聂祖娟.浅析路基检测方法的探讨［J］.安徽建筑，2008，15(2)：125-126.

［5］叶朝良.青藏铁路路基压实度检测方法的探讨［J］.路基工程，2005(6)：21-22.

［6］王驰，胡宇，张健.压实系数和地基系数双控路基压实质量的探讨［J］.山西建筑，2007，33(27)：293-294.

［7］曹建平.用于高速公路填石路堤的K30试验检测方法［J］.贵州工业大学学报(自然科学版)，2007，36(2)：99-102.

［8］程远水，朱忠林，张千里，等.提速线路路基检测评估方法及适用条件分析［J］.铁道建筑，2007(1)：74-76.

［9］彭志鹏.CFG桩处理中等压缩性土地基试验研究［J］.铁道建筑，2009(7)：13-18.