基于RBF神经网络的转子-轴承系统故障诊断

江帆，李伟，曹保钰，王泽文

(中国矿业大学 机电工程学院，江苏 徐州 221116)

转子系统是旋转机械的核心部件，常见故障为转子不对中和不平衡。滚动轴承是旋转机械中常见的通用部件之一，其运行状态直接影响机械设备的整体性能，因而对于机械设备的转子-轴承的故障诊断十分重要[1-3]。

近年来，由于旋转机械中异常振动引发的事故频发，对转子-轴承系统研究的重要性逐渐被认识到[4]。文献[5]对不平衡转子-轴承系统非线性行为进行了研究，并利用油膜力模型研究了转速、转子偏心及综合参数对转子-滑动轴承系统的非线性动力学行为的影响。文献[4，6]分别对转子-轴承系统的动力学进行了研究，对转子系统的动态设计与故障诊断提供了参考。在上述研究基础上，对旋转机械的不平衡转子-滚动轴承系统的故障行为进行了研究，提出通过快速Fourier变换(Fast Fourier Transform，FFT)提取旋转机械的故障特征信号，结合径向基函数(Radial Basis Function，RBF)神经网络实现转子-轴承系统的故障诊断。

1 FFT

对于非周期信号，不能简单地采用三角形式或指数形式的Fourier级数的复振幅来表示信号的频谱，通过频谱密度函数可以推导出Fourier变换[7]，其定义为

(1)

式中：F(jω)即为f(t)的频谱密度函数。对f(t)进行Fourier级数展开，有

(2)

(1)式和(2)式即为Fourier变换，前者为正变换，后者为逆变换。

传统Fourier变换计算量大，因而工程应用中常用的是FFT，其常用基2算法和分裂基算法[8]。

2 RBF神经网络

RBF神经网络是由Moody J和Darken C于20世纪80年代末提出的一种局部逼近网络[9]，其具有结构简单、学习能力强、收敛速度快和能够以任意精度逼近任意连续函数等优点。典型的RBF神经网络由输入层、隐层和输出层组成，其中输入层的节点个数由输入信号的维数决定，隐层的节点个数由描述实际问题的需要自动确定，输出层由目标输出决定[10]，其结构如图1所示。

图1 RBF神经网络结构

RBF神经网络属于分布式核函数学习模型，输入模式分布在以核为中心的邻节点空间。x为网络的n维输入，y为m维输出。对于RBF神经网络隐层的节点i，其输出值为n维输入向量x与网络隐层节点中心Ci的组合运算，其运算形式为[11-12]

(3)

式中：qi为隐层节点的输出；Ci为隐层第i个节点的中心，其中i= 1, 2，…，S；σ为Gauss函数方差。

输出层节点的输出值由隐层节点线性组合得到，计算公式为

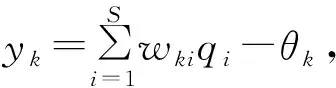
(4)

式中：yk为输出层第k个节点的输出值；θk为输出层第k个节点的阀值；wki为qi到yk的连接权值。

3 基于RBF神经网络的转子-轴承系统故障诊断方法

在信号处理中,Fourier变换能把信号按正弦展开成不同的频率值，将信号从时域变换到频域[7]，因此可以从频率的角度观测信号并提取表征信号的特征量。

3.1 故障特征向量的提取

由非周期信号的Parseval定理表明，非周期信号在时域中的信号能量与频域中的信号能量相等，即

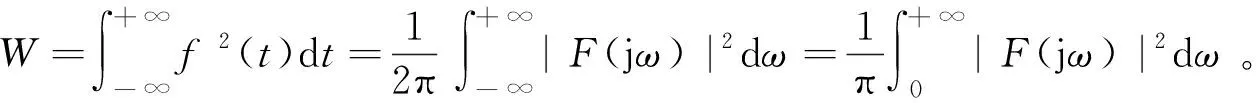
(5)

将采集的振动信号进行FFT处理，根据轴的转动频率确定转子转动的基频，分别提取第1～15个倍频附近的频率信号能量作为特征值，倍频附近能量的提取算法为

(6)

式中：W(I)为第I个倍频附近的能量值；ωn为基频；ωc为倍频余量。

3.2 RBF神经网络故障诊断

将提取的特征信号分为训练样本和测试样本，并用训练样本训练RBF神经网络直到达到要求的输出精度。最后用测试样本测试训练好的网络，实现转子-轴承系统的故障诊断。

4 故障诊断实例

4.1 数据采集和特征提取

为了验证所提转子-轴承系统故障诊断方法的可行性和有效性，在美国Spectra Quest公司生产的旋转故障模拟试验台(MFS，图2)上对转子-轴承系统中转子不平衡故障、轴承内圈故障以及转子不平衡和内圈混合故障进行了模拟试验。

1—三相异步电动机；2—变频器；3—激光转速计；4—联轴器；5—轴；6—转子；7—滚动轴承；8—信号转接口；9—计算机(相关软件)

试验设定转子的转速为594 r/min，转子-轴承系统的工作状态为：正常、转子不平衡故障1和2、轴承内圈故障以及混合故障1和2。转子不平衡故障1和2为转子两种不同程度的不平衡，通过在转子上安装大小不同的质量块实现；混合故障1和2为轴承内圈故障和转子不平衡故障1，2的混合故障。振动信号由安装在试验台轴承支架传感器基座上的加速度传感器测量，采样频率为1 kHz，单次采样时间为1 s。转子-轴承系统6种运行状态的原始振动信号如图3所示。

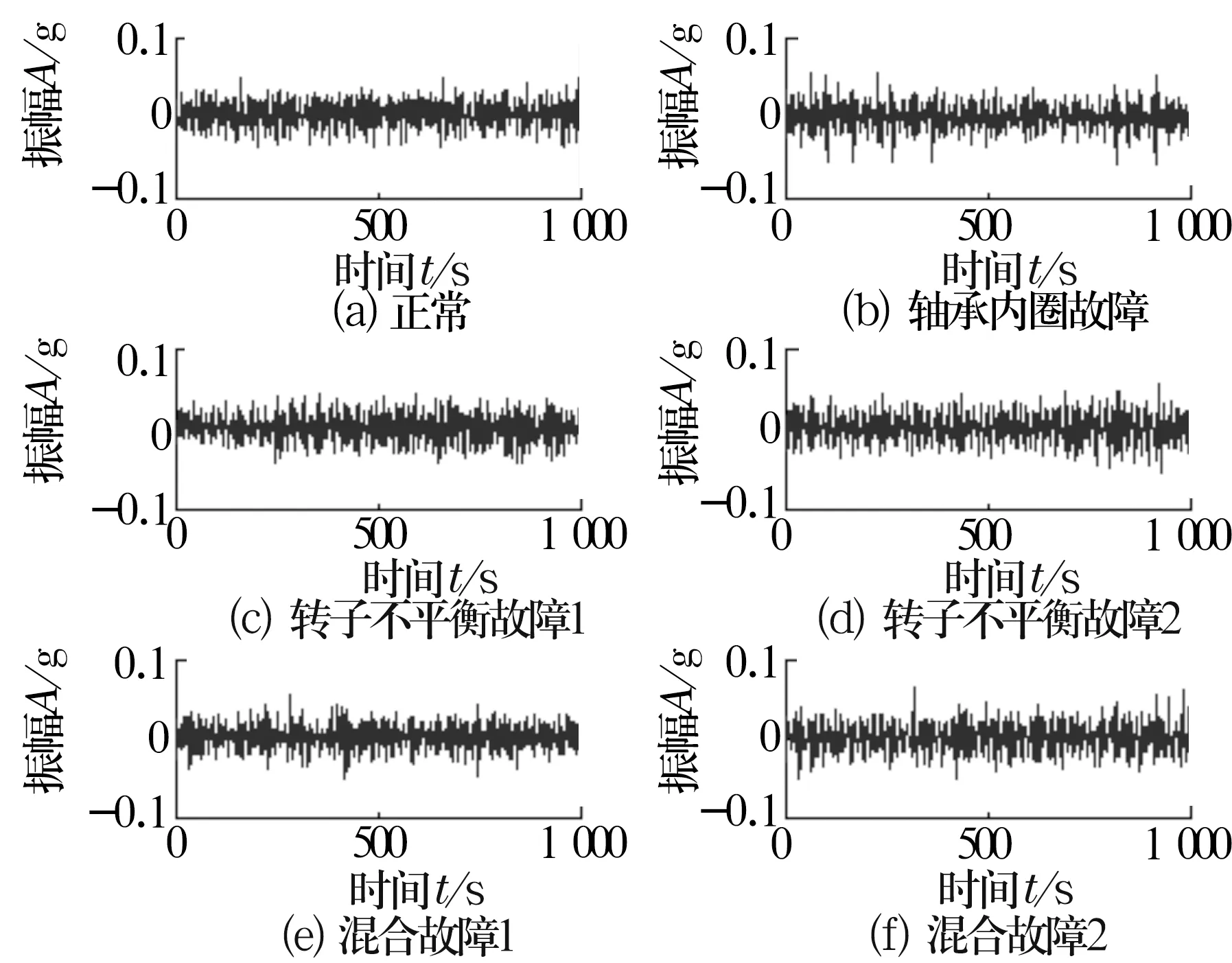
图3 振动信号

图4为图3中振动信号经过FFT处理得到的幅值-频率图。由图可知，转子-轴承系统在10，20 Hz等其他倍频及周围的频率变化特征明显，故倍频及周围的频率能量(图5)可作为故障的特征向量。试验在倍频余量为0和0.3ωn时分别制作了69组振动样本，每一组样本包含15个属性，分别为第1～15个倍频及周围能量值。

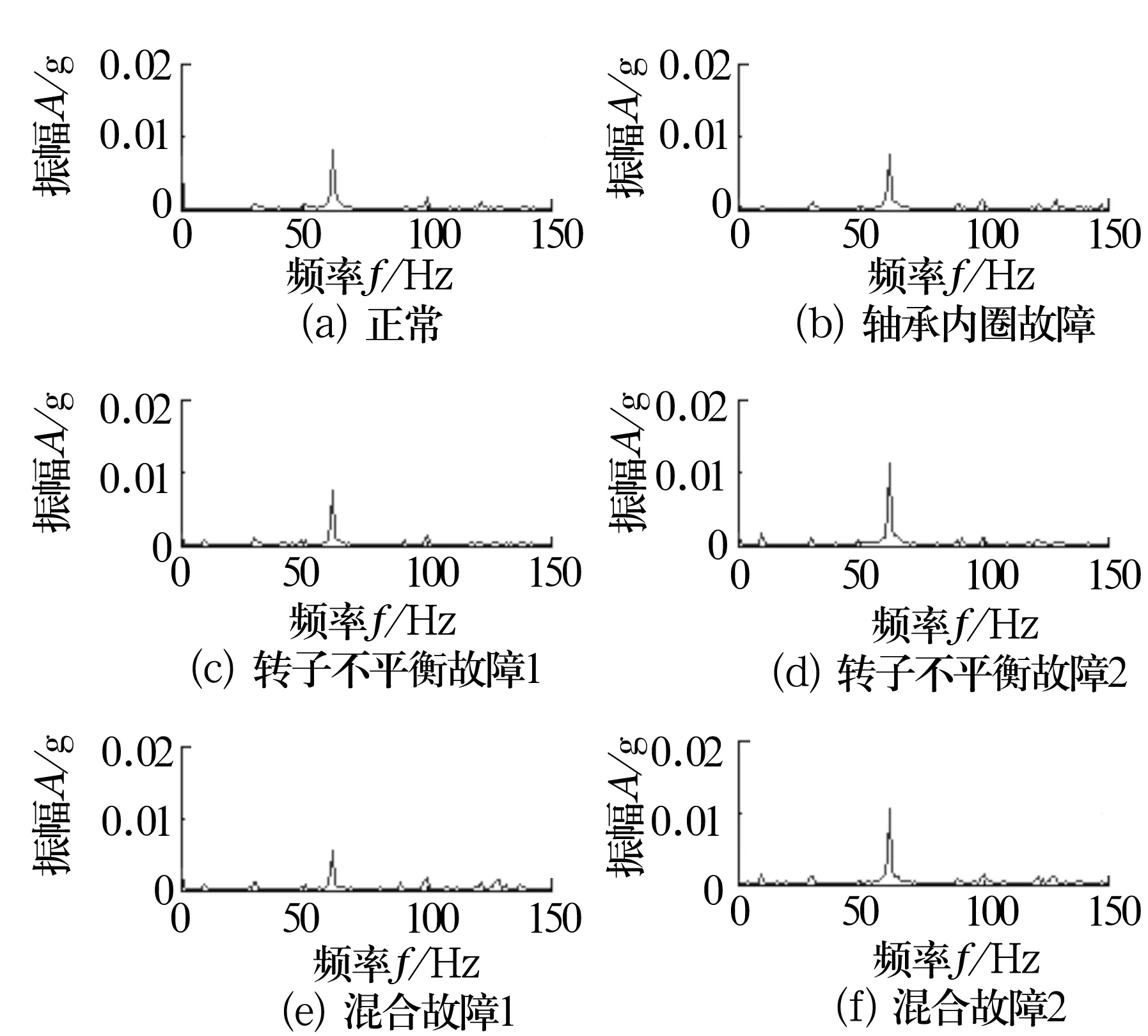
图4 频率信号

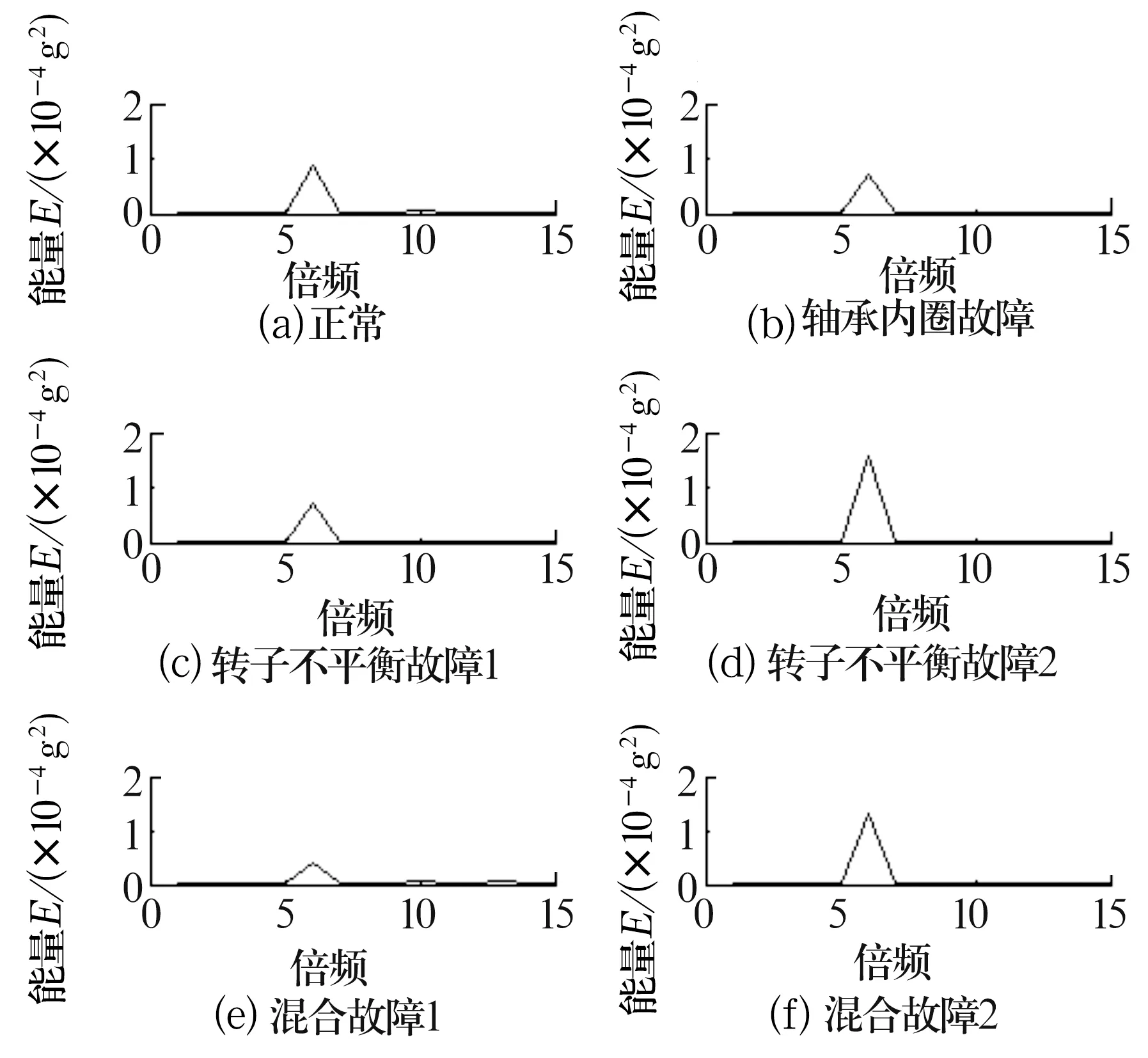
图5 倍频及附近的能量

4.2 故障诊断分析

将得到的69组振动信号特征样本分为58个训练样本和11个测试样本，分别对RBF神经网络进行训练和测试。RBF神经网络输入层为15个神经元，输入矩阵为xj={xj1，xj2，…，xj15}，其中j=0，…，M，M为训练或者测试样本的个数。输出层为6个神经元，分别用(100000)，(010000)，(001000)，(000100)，(000010)和(000001)表示正常、轴承内圈故障等6种状态的目标输出。部分网络的训练数据见表1。

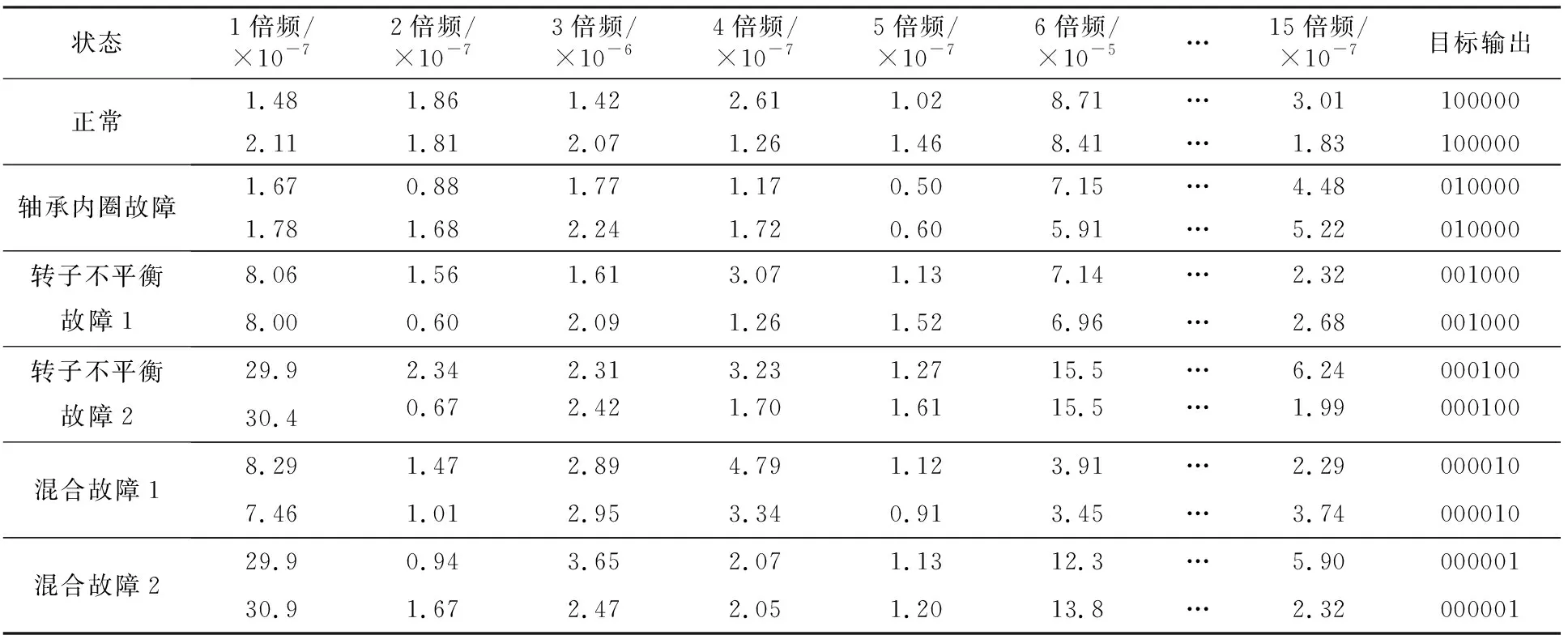
表1 部分网络的训练数据

获得训练样本和测试样本后，用训练样本训练RBF神经网络，然后用测试样本测试训练好的神经网络，测试结果见表2。

表2 RBF神经网络测试结果

由表2可知：将经FFT处理所求得的倍频能量谱作为故障信号的特征量，经过RBF神经网络的训练和测试表明，倍频能量谱和RBF神经网络对不平衡转子-轴承系统的故障诊断具有较高的正确率，能够区分正常状态、不同程度的两种转子不平衡故障和两种混合故障，相比直接用倍频处频率的幅值作为特征量的诊断效果更好。

5 结束语

通过对转子-轴承系统振动信号的研究，提出一种基于倍频附近的能量和RBF神经网络的转子-轴承故障诊断方法。由FFT得到振动信号的频谱图，分别提取第1～15个倍频在±0.3ωn范围内的能量作为RBF故障诊断网络的特征向量，从而实现故障诊断。试验表明，该方法的故障诊断结果与转子-轴承系统的实际运行状态具有较好的一致性，而且比单独使用倍频处的幅值作为特征值具有更好的诊断效果，从而证明了所述故障诊断方法的可行性和有效性。为了提高故障诊断的可信度和鲁棒性，在今后可进行多传感器数据融合研究。