多排滚子转盘轴承承载能力的计算

汪洪，李颖，田仁

(1.洛阳LYC轴承有限公司，河南 洛阳 471039；2.国电联合动力技术有限公司，北京 100039)

多排滚子转盘轴承是指轴向载荷和倾覆力矩由多排圆柱滚子承受的大型转盘轴承，其典型结构是三排滚子转盘轴承。为了承受更大的轴向载荷和倾覆力矩，主、辅推力滚子都可改为多排。多排滚子转盘轴承结构紧凑，承载能力大，使用范围正日益扩大。为了提高此类轴承的设计水平，必须对轴承的受力情况进行深入分析计算。文献[1]介绍了普通转盘轴承的滚动体载荷分布的计算方法。为了便于手工计算，该文假设主、辅推力滚子组的节圆直径是相同的，而实际设计时两者往往不同，因此其计算存在一定的误差。当主、辅推力滚子分别为多排时，文献[1]介绍的算法则无法适用。在此重点探讨主、辅推力滚子均为多排的转盘轴承的承载能力计算方法，此方法同样适用于普通三排组合滚子转盘轴承的计算。

1 滚子载荷分布的计算

1.1 滚子载荷与弹性接触变形的关系

设滚子承受的载荷为P，接触弹性变形为δ，则根据文献[2]，两者存在如下关系

P=Kδ1.1，

(1)

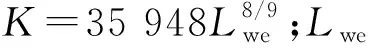
1.2 单排滚子的受力计算

为简化计算，假设轴承的套圈均为刚体，滚子与套圈间不存在间隙。设套圈在轴向载荷和倾覆力矩作用下的轴向位移为δa，角位移为θ，则受载最大的滚子的弹性变形量为

(2)

式中：Dpw为单排滚子组节圆直径。

位置角φ处的滚子的弹性变形量为

(3)

将(2)式代入(3)式，得

(4)

(5)

式中：ε为载荷分布参数。ε反映了单排滚子载荷分布的状态，当0<ε<1时，一排滚子中只有部分滚子受力；当ε≥1时，所有的滚子均受力；当ε=∞时，轴承仅承受纯轴向载荷。

单排滚子轴向力的合力F为

F=∑P(φ)=PmaxZJ0(ε)，

(6)

式中：Z为单排滚子的数量。

单排滚子合成的力矩M为

0.5PmaxDpwZJM(ε),

(7)

cosφdφ。

由此，当已知单排滚子最大滚动体载荷Pmax和载荷分布参数ε时，即可求出单排滚子的合成轴向力和倾覆力矩。

1.3 多排滚子载荷分布的计算

转盘轴承通常包含主、辅推力滚道，主推力滚道主要用来承受轴向载荷和倾覆力矩，辅推力滚道则主要用来承受倾覆力矩。

设主推力滚道由n排滚子组成，最外侧一排滚子的滚子组节圆直径是Dpw1，载荷分布参数是ε1，则

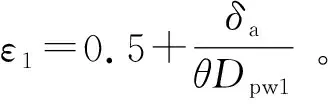
(8)

设主推力滚道第i排滚子的滚子组节圆直径是Dpwi，载荷分布参数是εi，则有

(9)

由(8)和(9)式得

(10)

(11)

由(8)和(11)式得

(12)

若已知主推力滚道最外侧一排滚子的载荷分布参数ε1，其余各排滚子的载荷分布参数便可由(10)和(12)式求得。

由(2)和(5)式得δmax=εθDpw。

设主推力滚道第i排滚子的最大弹性变形量为δmaxi，则δmax1=ε1θDpw1；δmaxi=εiθDpwi，故

(13)

设主推力滚道第i排滚子受载最大的滚子的载荷为Pmaxi，由(1)和 (13) 式得

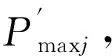
由 (6) 式得主推力滚道第i排滚子的轴向合力为

Fi=PmaxiZiJ0(εi)=Pmax1CiZiJ0(εi);

辅推力滚道第j排滚子的轴向合力为

所有滚子的轴向合力应与套圈承受的轴向力Fa相平衡，因此

(14)

同理，由 (7)式得

Mi=0.5PmaxiDpwiZiJM(εi)=

0.5Pmax1CiDpwiZiJM(εi),

根据力矩的平衡关系，各排滚子的合力矩应与外力矩Ma相平衡，即

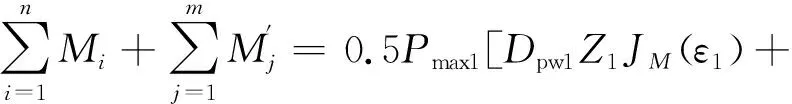
(15)

将 (15) 式除以 (14) 式得

(16)

(16)式是求解多排滚子转盘轴承载荷分布的基本方程式。当轴承的外载荷Fa和外力矩Ma已知时，其是关于ε1的一元非线性方程。利用Newton迭代法等数值算法可求出唯一的ε1值，进而求出各排滚子的载荷分布。

2 接触强度计算和静承载曲线绘制

2.1 接触强度的计算

当转盘轴承的外载荷已知时，运用上述滚子载荷分布的计算方法，可以求出作用于滚子上的最大载荷Pmax1(对于多排圆柱滚子转盘轴承而言，当主推力滚子存在多排时，由于通常滚子的长度取相同的值，滚子组节圆直径最大的一排滚子受到的载荷最大)。根据文献[3]，钢制圆柱滚子与平面的最大接触应力σmax可简化为

(17)

式中:Dw为滚子的直径。

2.2 静承载能力曲线的绘制方法

静承载能力曲线是转盘轴承选型的重要依据。转盘轴承受到的径向力通常相对较小，因此绘制静承载曲线时，仅考虑轴向力和倾覆力矩。取安全系数fs=1，则静承载曲线上每一点对应的载荷应恰好使得受载最大的滚子的最大接触应力达到其许用接触应力[σmax]。由(17)式知，滚子的最大载荷Pmax为

在(14)和(15)式中取Pmax1=Pmax，则有

(18)

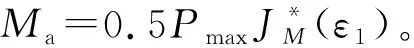
(19)

(18)和(19)式即构成了主推力滚道以ε1为参数的静承载曲线的参数方程式。

当轴承同时承受很大的倾覆力矩和很小的轴向力时，辅推力滚道上的接触应力会大于主推力滚道上的接触应力。因此，应同时构造辅推力滚道以ε1为参数的静承载曲线，并求出两条曲线的交点坐标，最终形成折线形式的完整静承载曲线。图1为某六排滚子转盘轴承的静承载曲线。

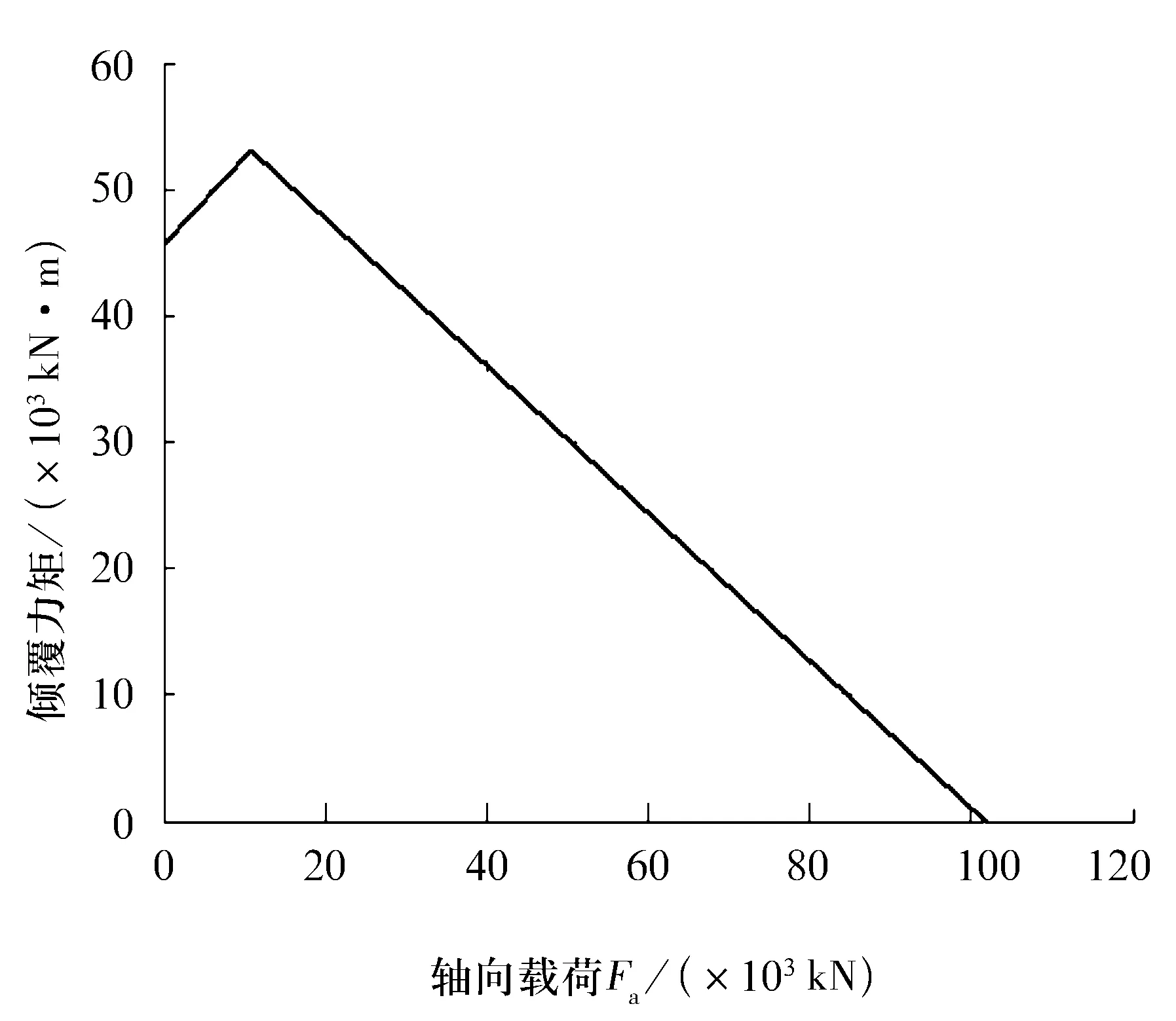
图1 静承载能力曲线

3 工作寿命的估算和动承载曲线的绘制方法

转盘轴承的工作寿命也是其重要的性能指标。下面以Lundberg-Palmgren的疲劳寿命理论为基础，研究其寿命计算问题。每一排滚子分别与内、外圈的滚道相接触。在进行寿命估算时，首先分别计算出每条滚道的额定寿命，最后根据乘法规则计算出整套轴承的额定寿命。

3.1 滚道的额定滚子载荷Qc[3]

(20)

式中：B为常数。

3.2 每个滚道的当量滚子载荷Qe

对于旋转的套圈，其滚道当量滚子载荷Qe1为

dφ]1/4。

静止套圈滚道的当量滚子载荷Qe2为

dφ]2/9=PmaxJ2(ε)，

3.3 单个滚道的额定寿命

单个滚道的额定寿命L10为

(21)

3.4 整套轴承的额定寿命

对于单个滚道而言，其使用概率和使用寿命之间存在如下关系

(22)

式中：S为滚道的使用概率;LS为使用概率为S时的寿命；e=9/8。

如图1所示的多排滚子转盘轴承，其上排滚子对应的上、下两侧滚道是主推力滚道。下排滚子上、下两侧滚道是辅推力滚道。 主推力滚道有3排滚子, 每排滚子接触的上侧滚道是旋转滚道,下侧则是静止滚道，即主推力滚道共有6条。

由(22)式知，对于每一滚道有

式中：下标k=i,j，分别代表主、辅推力滚道;下标x代表滚子组的排号;下标y=1,2，分别代表旋转、静止滚道。

对于整套轴承，同样有

式中：下标b代表整套轴承。

由于所有滚道中任一滚道出现疲劳失效时，就可认为整套轴承出现了疲劳失效，故有LSb=Lkxy，则整套轴承的额定寿命L10b为

(23)

(23)式是绘制转盘轴承动载荷承载曲线的基本方程式。在绘制动载荷承载曲线时，L10b为定值(通常取为30 000转)，对于给定的轴向力Fa，(23)式是关于倾覆力矩Ma的一元方程，求解后可获得唯一解。求解出若干组(Fa,Ma)值后，依次连接即绘制出动载荷承载曲线。图2为某六排滚子转盘轴承的动载荷承载能力曲线。

图2 寿命为30 000转时的动载荷承载曲线

4 结束语

多排滚子转盘轴承是近年为配合超大吨位起重机械的开发而研发的新型转盘轴承。由于缺乏设计理论的支持和计算的复杂性，通常采用经验式计算。文中提出的理论计算方法为实现此类轴承从经验式设计向理论设计的过渡提供了帮助。