基于IMM多传感器顺序粒子滤波跟踪机动目标算法*

陆新东，胡振涛，刘先省，金 勇

（河南大学计算机与信息工程学院，河南开封 475004）

0 引言

机动目标跟踪中，被估计对象一般存在多种运动模式且随时可能在各模式间切换，为有效描述机动目标状态变化过程，通常将跟踪系统建模为多模型。目前应用较为普遍的是交互式多模型（interacting multiple models，IMM）［1］，针对不同的应用背景，其子滤波器结合卡尔曼滤波器或扩展卡尔曼滤波器，但对于强非线性系统，这类算法的滤波精度不高。考虑粒子滤波器不受系统非线性和噪声类型限制的优点［2～4］，Yang N等人利用粒子滤波替换 IMM 中的子滤波器，提出IMM粒子滤波 （interacting multiple model particle filtering，IMMPF）算法［5，6］，并衍生出 IMM卡尔曼—粒子滤波器等改进算法［7］，改善强非线性对跟踪精度的影响。

然而在实际工程环境中，单传感器受到传输误差、计算误差、环境噪声和人为干扰等影响，量测值存在不确定性因素，造成估计值与真实值间存在较大误差。随着多源信息融合技术的发展，多传感器系统成为多源信息融合领域的研究热点之一，如何利用多传感器量测数据实现复杂系统状态估计具有重要意义。熊伟等人基于多源信息融合技术，提出多传感器顺序粒子滤波算法、IMM分布式估计融合算法等［8，9］，此类算法可较好地解决强机动目标的状态估计问题，而对多模式运动的目标，估计精度不能保证。基于以上分析，本文在IMMPF基础上，结合多传感器量测的特点，提出一种基于IMM的顺序粒子滤波算法，进一步提取和利用多量测的冗余和互补信息，提高系统状态估计精度。

1 IMMPF算法的描述

IMM算法实质在于系统中模型并行滤波，通过模型概率对各模型滤波的输出进行估计综合，主要分为输入交互、模型滤波、模型概率更新和输出交互4个环节。

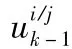
式中 ［·］T代表矩阵转置。在获取传感器量测后，计算模型j的残差及其协方差，则模型似然函数为

2 IMMSPF机动目标跟踪算法

考虑到复杂环境，采用单传感器系统必然会受到干扰，标准IMMPF算法及其改进算法，不可避免包含了整个采样过程中所有干扰，如何弱化随机扰动对系统的影响，多传感器系统是解决此问题的关键。由此，本文提出了一种基于IMM的顺序粒子滤波算法，即把单传感器系统，扩展到多个传感器系统，并利用顺序重抽样方法优化粒子的分布。这种处理方式优点在于:1）多传感器系统弱化单传感器系统量测中的不确定性扰动，增加系统量测的可靠性;2）重抽样方法改善粒子分布，提高系统的估计精度;3）算法适用于更加复杂的环境，增强算法的适用性。以下着重描述算法过程。

进而粒子权重可依据下式实现

对粒子权重归一化处理

由于重要性权重的方差会随着时间增大，将导致粒子退化，此时需要引入重抽样过程，其思想为保持粒子总数不变，删减权重较低的粒子数目，增加具有较高权重的粒子数目，从而降低重要性权重方差。目前，重抽样方法主要有残差重采样、系统重采样和多项式重采样等［11］，本文利用残差重抽样方法，抑制退化现象。

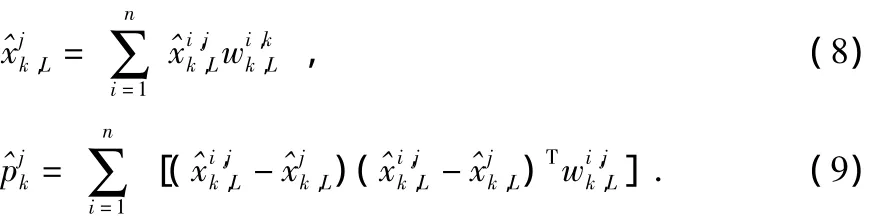
依据IMM算法框架，计算似然函数并更新模型j的权重

最终，利用各模型状态估计值计算被估计系统的当前状态

3 仿真结果与分析

为验证算法的可行性和有效性，仿真实验中采用同种类型不同参数的多个传感器组成量测系统，对比IMMPF和IMMSPF两种算法的跟踪精度。由CV模型和CT模型构成分段的目标机动模型，量测方程为非线性模型，多传感器系统建模如下

状态噪声协方差σ2=1和σ2=0.5下，图1、图2分别显示IMMPF算法和IMMSPF算法目标估计精度的均方根误差比较;表1和表2分别表示了两种算法状态估计精度的均方根误差均值的比较。由图1和图2看出:目标在1～18，35～50时刻弱非线性运动，新算法估计性能明显优于IMMPF算法，状态估计更加可靠;目标在18～35时刻强机动、多模型和非线性运动时，跟踪精度还能保持良好的滤波性能，相对弱机动运动时精度提高较少，总之，两种算法都能稳健地跟踪机动目标，新算法考虑利用最新量测信息与多传感器之间蕴含的冗余和互补信息，整体跟踪精度较高。对比两图可以直观地看出:在状态噪声较小的情况下，两种滤波算法跟踪精度都得到提高;由表1和表2中的定量分析结果看出:状态噪声减小，两种算法精度都得到提高，新算法在速度方面提高的较多，但是位置估计提高不明显，所以，在速度估计精度要求不高的情况下，可以选用精度较低的传感器，降低系统的成本。另外，随着传感器的增多，跟踪精度也会得到提高，但综合系统性能、计算量和造价等因素，传感器数量也不是越多越好，主要是实现精度和计算量等性能的平衡。

图1 σ2=1时两种算法精度对比Fig 1 Comparison of precision of two algorithms on σ2=1

图2 σ2=0.5时两种算法精度对比Fig 2 Comparison of precision of two algorithms on σ2=0.5

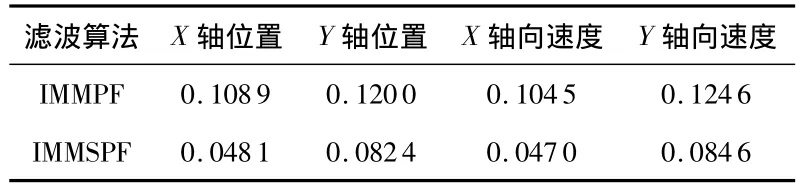
表1 σ2=1时状态估计RMSE均值对比Tab 1 Mean RMSE comparison of state estimation on σ2=1

表2 σ2=0.5时状态估计RMSE均值对比Tab 2 Mean RMSE comparison of state estimation on σ2=0.5

4 结论

本文通过IMM粒子滤波方法和多传感器顺序粒子滤波方法的有机结合，提出IMMSPF算法，并成功地引入到机动目标跟踪，较好地解决了单传感器量测系统的缺陷。新算法根据多次量测的随机性，弱化了单传感器受到干扰时不确定性的影响，并进一步提取量测间的冗余和互补信息优化粒子分布，从而提高状态估计的可靠性，最终增强系统跟踪强机动、多模型和非线性运动目标的能力。仿真结果表明:新方法有效地提高了系统状态估计的精度。

［1］Mazor E，Averbuch A，Bar-shalom Y.Interacting multiple model methods in target tracking:A survey［J］.IEEE Trans on Aerospace and Electronic Systems，1998，33（1）:103 －123.

［2］Bugallo M F，Xu Shanshan，Petar M D.Performance comparison of EKF and particle filtering methods for maneuvering targets［J］.Digital Signal Process，2006，16（10）:672 －678.

［3］刘喜梅，魏婉韵，于 飞.基于粒子滤波的分布式故障诊断［J］.传感器与微系统，2008，27（3）:30 －33.

［4］Yang N，Tian W，Jin Z.An interacting multiple model particle filter for maneuvering target location［J］.Measurement Science and Technology，2006，17（6）:1307 －1311.

［5］何 友，修建娟，张晶炜，等.雷达数据处理及应用［M］.北京:电子工业出版社，2006.

［6］刘贵喜，高恩克，范春宇.改进的交互式多模型粒子滤波跟踪算法［J］.电子与信息学报，2007，29（12）:2810 －2813.

［7］彭志专，冯金富，钟咏兵，等.基于IMM2PF的分布式估计融合算法［J］.控制与决策，2008，23（7）:837 －840.

［8］熊 伟，何 友，张晶炜.多传感器顺序粒子滤波算法［J］.电子学报，2005，33（6）:1116 －1119.

［9］刘先省，胡振涛，金 勇，等.基于粒子优化的多模型粒子滤波算法［J］.电子学报，2010，38（2）:301 －306.

［10］Arulampalam M S，Maskell S，Gordon N，et al.A tutorial on particle filters for online nonlinear/non-Gaussian Bayesian tracking［J］.IEEE Trans on Signal Processing，2002，50（2）:174 －188.

［11］胡振涛，潘 泉，杨 峰.将粒子残差一致性度量的滤波算法用于纯方位被动跟踪［J］.红外与毫米波学报，2010，29（1）:75－80.