一种基于改进蚁群算法的光网络波长路由分配算法
程 希 沈建华
(南京邮电大学通信与信息工程学院 南京 210003)
1 引言
IP数据业务的持续高速增长推动了光网络的持续快速发展。为了更好地适应未来各种高带宽、交互式和差异化服务质量(QoS)业务的需要,光网络正在向具有智能、灵活、透明和安全等特点的下一代光网络发展[1]。下一代光网络最重要的特征之一就是可以根据业务的需要,灵活地建立端到端的动态光通路以提供对上层业务的全光透明传输,并根据业务的QoS需求和网络资源的实时使用情况实现动态路由、流量疏导(traffic grooming)和保护恢复等功能。其中,路由与波长分配 (RWA)是下一代光网络中实现动态资源分配的核心问题。
RWA问题的核心是为光网络中到达的业务计算路由并分配波长,从网络优化角度而言就是在给定的波长数目和连接请求等约束条件下, 如何选择最优路由以使占用的资源(波长数或波长转换器数)最少,或者业务被阻塞的概率最小[2]。动态RWA问题已被证明是NP-C问题[3]。因此,最初的研究方法大多把 RWA问题分解为路由和波长分配两个子问题分别加以解决。也即先进行选路,解决路由子问题,然后在满足一定约束条件的情况下逐一为计算出的路由分配波长。文献[4]针对 RWA问题提出了新的数学模型——分层图模型,其基本思想通过将物理拓扑映射成若干分层图的方式,把一个复杂的问题分解成一个3维模型。文献[5]证明了分层图模型的主要缺点是在解决大型网络问题时耗费时间较长。随着包括遗传算法、模拟退火、神经网络、粒子群等启发式的算法的研究,结合分层图模型的启发式算法开始引入到光网络的RWA问题中。文献[6]提出了将一种改进的脉冲耦合神经网络(PCNN)算法引入到光网络路由选择中,并将波长分配与分层图模型相结合,通过改变PCNN神经元的点火方式以及控制自动波的传播时间来模拟路径代价,从而使得网络路由选择具有了PCNN的并行处理特性的优点,但仍然存在分层图模型耗费时间长的缺点。文献[7]将 RWA问题简化成为一个整数线性规划问题,并使用遗传算法解决多目标的 RWA问题。虽然实现了多目标优化,但是其仿真是基于静态的网络状态,且每个光纤上的波长数没有限制,与实际网络环境存在较大差异。针对基本的遗传算法的收敛性较差,常限于局部最优,以及随机性较强,不能快速找到所需要分配的波长等缺点,文献[8]针对环形网络提出了一个新的整数线性规划(ILP),核心思想是将路径集合进行分割并相应使用独立的集合计算来表示在最初网络中的 MIS(Maximal Independent Sets),具体实现时在变量数和约束条件数之间做了折中,在网络方面可以到达一定的伸缩性,计算时间短,但是只适用于环形网络。文献[9]提出了使用基本的蚁群算法解决 RWA问题,即首先初始化参数和计算路由表,然后使用基本的蚁群算法计算路由和波长分配,蚂蚁从源节点出发到达目的节点后再沿原路返回,主要关注算法的实时性。文献[10]提出了使用蚁群算法解决RWA问题,路由和波长分配的任务由每只蚂蚁同时负责完成。但是文献[9]和文献[10]都忽略了网络负载均衡问题。
本文提出了一种基于蚁群算法的SA-DRWA算法以解决光网络的动态 RWA问题。SA-DRWA算法的主要创新点是在蚁群算法的转移概率中加入了链路的空闲率作为约束条件,在保证网络中负载均衡的同时实现较低的网络阻塞率。论文的第1节是RWA问题概述;第2节介绍了SA-DRWA算法原理和算法的理论分析;第3节通过仿真分析了SADRWA算法性能,给出了与经典的Dijkstra+FF算法的对比;最后是全文的总结。
2 SA-DRWA算法
2.1 算法原理
由于光网络的 RWA问题包含了路由和波长分配两个子问题,不能直接使用传统蚁群算法。本文在考虑了波长分配和网络负载均衡等条件下,提出了基于蚁群算法的SA-DRWA算法,其核心思想是在蚁群系统的转移概率中增加链路的空闲率作为约束条件,并引入随机扰动防止搜索过早收敛于局部最优路径。算法中,每只蚂蚁同时负责完成路由和波长分配的任务[10],即蚂蚁在每个节点上,首先进行波长的判断,然后再进行路径上的选择(路由计算),这样可以将路由和波长分配这两个问题统一起来。此外,蚂蚁到达目标节点后按原路返回,若蚂蚁在选路过程中无路可选则自杀,即本次迭代失败。由于 RWA问题的目标是在源节点和目标节点之间建立一条可用的光通路,故初始化时把蚂蚁随机均匀地放置在源节点和目标节点。
定义
(1)信息素tijw(t)为t时刻节点(i,j)间路径上波长w的信息素量。
(2)链路空闲率Iijw(t)为t时刻节点(i,j)间路径上波长w的空闲率,由式(1)给出:

其中|Nijw|为链路Lij上波长w的总波长数,nijw(t)为t时刻链路Lij上波长w使用数。
(3)转移概率。在蚁群算法的转移概率中引入链路空闲率Iijw(t)作为新的约束条件,即t时刻处于节点i的蚂蚁k选择节点j的概率(t)由式(2)给出:
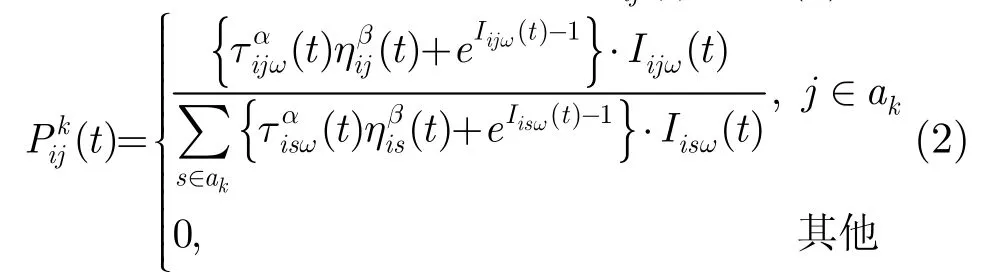
式中tijw(t)为t时刻路径(i,j)上w波长的信息素强度;a≥0为信息素启发因子,表示轨迹的相对重要性;b≥0为期望启发因子,表示能见度的相对重要性;ak表示t时刻蚂蚁可以选择的节点集(ak=C-Tabuk,C为与节点i存在链路的节点集,Tabuk表示当前搜索周期到时刻t为止蚂蚁所走过的节点集);hij(t)为链路(i,j)的启发函数,一般为距离的倒数[10]。
(4)蚁群系统状态转移规则。由于动态RWA问题的实时性要求较高,所以算法中迭代次数不能太多。当迭代次数较少时,蚁群算法的搜索又容易收敛于局部最优路径,因此本文提出引入随机扰动,以在迭代次数较少时防止路径搜索过早收敛于局部最优路径:即蚂蚁在选路时,在可选的节点中随机选择下一个节点。算法的状态转移规则可以表示为:位于节点r的蚂蚁通过式(3)的3种选路规则选择下一个将要移动到的节点s。

其中q是在[0, 1]区间均匀分布的随机数,q0和q1是参数( 0 ≤q0≤ 1 ,q0≤q1≤ 1 ),S为根据式(2)给出的概率分布所选出的一个随机变量。
算法的伪代码如表1所示。算法的终止条件是到达指定的迭代时间Tc或迭代的次数Nc。若蚂蚁k当前节点与目标节点直接相连,即目标节点属于可选节点集合,若波长lk还有空闲则下一节点为目标节点;若没有空闲的波长lk但节点具有波长转换功能则下一节点也为目标节点,并再选择一个波长。

表1 SA-DRWA算法的伪代码
2.2 理论分析
网络可记为G=(V,E,W),其中V为网络节点集,E为双向链路集,W为每条链路的波长数。Dijkstra算法的复杂度为O(V2),当节点没有波长转换功能时,FF(First Fit)算法的复杂度为O(W),则Dijkstra+FF算法复杂度为O(V2+W) ~O(V2);当节点具有波长转换功能时,FF算法的复杂度为O(VW), Dijkstra+FF算法复杂度为O(V2+VW)~O(V2)。故Dijkstra+FF算法复杂度为O(V2)。
当节点没有波长转换功能时,最坏情况下,算法中每只蚂蚁的复杂度为O(V2+ 2V+W)~O(V2),计算如下:初始化蚂蚁的禁忌表O(V),选择波长O(W),波长一旦选定,就不需考虑波长选择问题,蚂蚁每一跳为O(V),局部信息数更新为O(1),蚂蚁最多V-1跳,即O(V),全局信息素更新为O(V)。当节点具有波长转换功能时,最坏情况下,算法中每只蚂蚁的复杂度为O(V2+ 2V+VW)~O(V2),计算如下:初始化蚂蚁的禁忌表O(V),最多所有节点具有波长转换功能,选择波长O(VW),蚂蚁每一跳为O(V),局部信息数更新为O(1);蚂蚁最多V-1跳,即O(V);全局信息素更新为O(V)。所以每只蚂蚁的复杂度为O(V2),而文献[9]中每只蚂蚁的复杂度为O(2V2)。算法的最大迭代次数为Nc,蚂蚁数量为M,整个算法的复杂度为O(Nc MV2),算法的时间复杂度比文献[9]的小,比Dijkstra+FF算法大。
蚁群算法中信息素强度限制是保证任意的节点i和j之间满足:t0≤tij(t) ≤ 1 /Cbs,其中t0取1/(nCnn)算法有较好的性能,Cnn为由最近邻方法得到的路径长度,Cbs为最优路径长度[10]。类似地,路径(i,j)上波长w的信息素量tijw(t)也具有同样的限制:t0≤tijw(t) ≤ 1 /Cbs。启发函数hij(t)一般为距离的倒数[11],由于节点间距离远大于 1,因此tijw(t)和hij(t)都是小于1且大于0的小数。
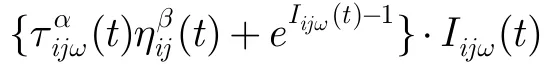
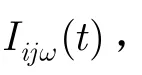
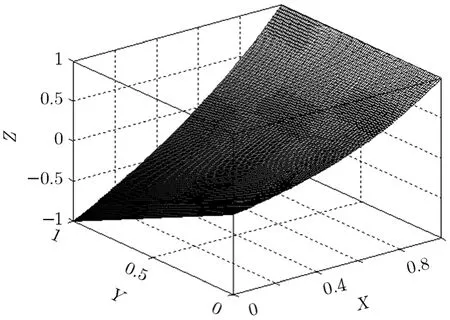
图1 函数 z = ( y + e x -1)x- y 图
如图1所示,当x=0,y=0时,z=0,可知:存在一系列点(x,y)使 (y+ex-1)x-y=0成立。设(x0,y0)是等式 (y+ex-1)x-y=0的一个解,x0∈(0,1),y0∈(0,1),由图可得当x<x0时, (y0+ex-1)x-y0<0,即(y0+ex-1)x<y0;当x>x0时, (y0+ex-1)x-y0<0,即(y0+ex-1)x>y0。也就是说,当x(链路空闲率)小于某一个值时,链路忙,SA-DRWA算法的转移概率小于基本ACS算法的转移概率;当x大于某一个值时,链路空闲,SA-DRWA算法的转移概率大于基本ACS算法的转移概率。由于蚁群算法是一种概率型算法,转移概率越大则选择此链路的概率也就大,因此SA-DRWA算法可以使蚂蚁选中链路空闲率高(业务量小)的路径概率增大,从而实现了网络负载的均衡。

3 算法性能仿真
将SA-DRWA算法与Dijkstra+FF算法进行了网络阻塞率及资源利用率的性能仿真。仿真中使用的分别是16个节点32条链路规则对称的网格网络,16个节点21条链路的NSFNET网络, 20个节点22条链路的Cernet网络和28个节点41条链路的pan-European网络[12],分别如图2所示。4种网络拓扑结构中均为节点间有4条光纤相连,每一条光纤中有6个可用波长。
仿真时假设业务请求按泊松分布到达网络,业务请求一旦被拒绝,则立即被丢弃,即无等待队列,所有的节点没有波长转换功能,即满足波长一致性约束。节点数与蚁群数之比为1.5[13];最大迭代次数200,其他参数设置参考文献[13]。为不失一般性,仿真初始时假设网络中已有已知呼叫业务产生。图3分别给出了4种拓扑结构中阻塞率和资源利用率的仿真结果。由于业务请求的源节点和目标节点是随机产生的,带有一定的随机性,图3中的数据是多次(100次)统计平均的结果。
从图3(a)中可以看出,对于规则对称网格网络:当业务强度比较小时,SA-DRWA算法阻塞率几乎为0,较Dijkstra+FF算法最大有0.23的改进,且在较大范围业务强度情况下,都有显著改进。图3(b)中可以看出,SA-DRWA算法的资源利用率比Dijkstra+FF算法高,尤其是在中等业务强度下,改善最大达到了0.23。
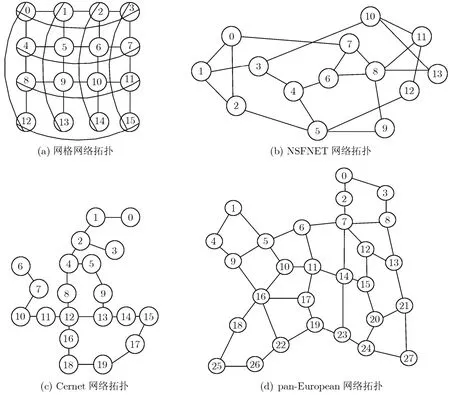
图2 仿真使用的网络拓扑结构
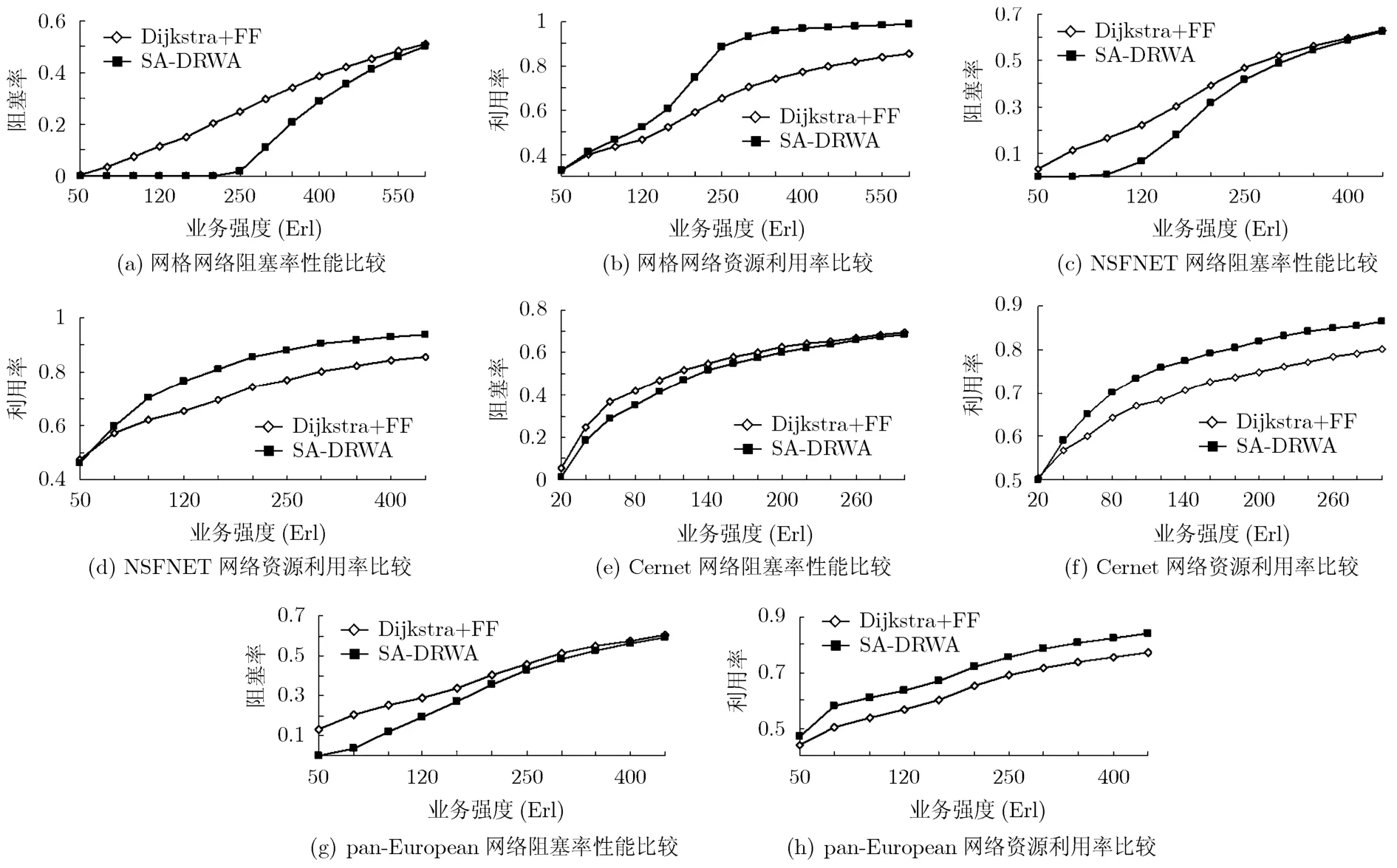
图3 网络阻塞率和资源利用率的对比
从图3(c)中可以看出,对于NSFNET网络,当业务强度比较小时,SA-DRWA算法得到的网络呼叫阻塞率几乎为0,在中等业务强度下, SA-DRWA算法也比Dijkstra+FF算法性能有所改善;图3(d)中可以看出,SA-DRWA算法的资源利用率比Dijkstra+FF算法提高了0.12。
从图3(e)中可以看出,对于Cernet网络中,在业务强度比较小时, SA-DRWA算法比 Dijkstra+FF算法最多改善了0.08,但在中等业务强度下,改善并不是很明显;图3(f)中可以看出,SA-DRWA算法的资源利用率提高了约0.07。
从图3(g)中可以看出,对于pan-European网络中,中低业务强度下SA-DRWA算法比Dijkstra+FF算法最多改善了约 0.08,但在业务强度较大时,改善并不是很明显。图 3(h)中可以看出,SA-DRWA算法的资源利用率约提高了0.08。
总的来看,SA-DRWA算法与Dijkstra+FF算法相比,资源利用率在各种业务量负荷情况下都有较为显著的提高。而阻塞率性能在业务量较小时改善较为明显,当业务强度较大时,由于受到波长一致性和链路可用波长总数等的限制,性能改善有限。对于不同的网络拓扑而言,SA-DRWA算法在规则对称网格网络中阻塞率性能和资源利用率改善最明显,阻塞率最大降低了 0.23,资源利用率最大提高了0.23。
4 结束语
动态 RWA是下一代光网络需要解决的核心问题之一,蚁群算法以其并行性、鲁棒性等特点成为解决光网络动态 RWA问题的有效手段。本文提出了一种基于蚁群算法的SA-DRWA算法,通过引入链路空闲率和随机扰动,使其能够很好地解决智能光网络的 RWA问题。理论分析和数值仿真表明:与Dijkstra+FF算法相比,SA-DRWA算法不仅可以有效地实现光网络的负载均衡,同时可以有效降低阻塞率和提高网络资源的利用率,尤其是在规则对称的网格网络中可以获得最佳的性能改善,阻塞率最大降低了0.23,资源利用率最大提高了0.23。
[1]黄善国, 顾畹仪, 等. IP数据光网络技术与应用[M]. 北京: 人民邮电出版社, 2008: 45-48.
Huang Shan-guo, Gu Wan-yi,et al.. IP Data Optical Network Technology and Application[M]. Beijing: Posts &Telecommunications Press, 2008: 45-48.
[2]单广军, 朱光喜, 刘德明, 等. 基于关键链路预测的动态路由和波长分配算法[J]. 电子学报, 2010, 38(7): 1673-1677.
Shan Guang-jun, Zhu Guang-xi, Liu De-ming,et al.. An dynamic routing and wavelength assignment algorithm based on key links forecasting[J].Acta Electronica Sinica, 2010,38(7): 1673-1677.
[3]Ramaswami R and Sivarajan K N. Optical Networks: A Practical Perspective[M]. San Francisco, CA, Morgm KouJkann Publishers Inc., 2002: 255-380.
[4]Chen Chien and Banerjee S. A new model for optimal routing and wavelength assignment in wavelength division multiplexed optical networks[C]. International Conference on Computer Communications96(INFOCOM96), San Francisco,CA, USA, 1996: 164-171.
[5]Xu Shi-zhong, Li Le-min, and Wang Sheng. Dynamic routing and assignment of wavelength algorithms in multifiber wavelength division multiplexing network[J].IEEE Journal on Selected Areas in Communications, 2000, 18(10):2130-2137.
[6]杨勇, 张晓萍. 基于改进PCNN算法的光网络RWA问题的研究[J]. 微计算机信息, 2010, 26(3): 105-106.
Yang Yong and Zhang Xiao-ping. Study on RWA of optical network based on improved Pulse-Coupled Neural Network[J].Micro-computer Information, 2010, 26(3): 105-106.
[7]Barpanda R S, Turuk A K, Sahoo B,et al.. Genetic algorithm techniques to solve routing and ravelength assignment problem in wavelength division multiplexing all-optical networks[C]. Communication Systems and Networks(COMSNETS), Bangalore, 2011, 3: 1-8.
[8]Yetginer E, Liu Ze-yu, and Rouskas G N. Fast exact ILP decompositions for ring RWA[J].Optical Communications and Networking, 2011, 3(7): 557-586.
[9]Triay J, and Cervelló-Pastor C. An ant-based algorithm for distributed routing and wavelength assignment in dynamic optical network[J].IEEE Journal on Selected Areas in Communications, 2010, 28(4): 542-552.
[10]郑滟雷, 顾畹仪, 连伟华, 等. 采用蚁群算法解决光网络中动态及分布式 RWA问题的方法[J]. 北京理工大学学报, 2009,29(12): 1104-1109.
Zheng Yan-lei, Gu Wan-yi, Lian Wei-hua,et al.. Ant colony algorithm distributed strategy for solving RWA problem in optical WDM network[J].Transactions of Beijing Institute of Technology, 2009, 29(12): 1104-1109.
[11]Dorigo M, and Stützle T 著, 张军, 等, 译. 蚁群优化[M]. 北京: 清华大学出版社, 2007: 21-58.
[12]De Maesschalck S. Pan-european optical transport network:an availability-based comparison[J].Photonic Network Communications, 2003, 5(3): 203-225.
[13]段海滨. 蚁群算法原理及其应用[M]. 北京: 科学出版社, 2005:103-116.
Duan Hai-bin. Principle and Application of Ant Colony Algorithm[M]. Beijing: Science Press, 2005: 103-116.

