莱斯信道下多载波异步发射分层空时码设计

刘 田 莫韬甫 文 荣 唐友喜

(电子科技大学通信抗干扰技术国家级重点实验室 成都 611731)

1 引言

在下一代移动通信系统中，由于基站与移动终端的距离逐渐减小，造成收发信机之间存在直射(Line Of Sight, LOS)路径的概率增大[1]。对于分层空时码，LOS路径的存在使信道矩阵的条件数增大，涉及信道矩阵求逆操作的检测算法(如迫零检测)性能恶化，检测甚至失效[2]。STBC(Space-Time Block Codes), STTC(Space-Time Trellis Codes)和波束成形(Beamforming)等以利用信道分集增益为目的的空时码虽然可以在莱斯信道下甚至是纯 LOS情况下获得稳定的性能[3]，但是其频谱效率不及以空间复用为目标的分层空时码技术(Vertical Bell laboratories LAyered Space-Time, V-BLAST)[4]。

为了能让V-BLAST类高频谱效率空时码在莱斯信道下有效工作，Gesbert[5]提出了一种采用闭合形式的近似最小误差接收算法；Akhtar等人[6]提出通过调整发射信号的功率和相位以改变星座图的方法来解决。但这两种方法都是把LOS分量当成不利因素加以改进。文献[7]采用各子流时间上的异步发射，获得了比同步V-BLAST更大的分集度，突破了接收天线数不小于发射天线数的限制[8]，说明了该结构应用于莱斯信道的可能性；但没有具体给出其在莱斯信道下的分析和仿真结果。文献[9]利用天线间时域成型脉冲的相关性实现了分层空时码在莱斯信道下的有效接收，使LOS分量成为一种对分层空时码有益的信道因素，但其仅讨论了平坦衰落信道下的性能分析结果，对于更为现实的频率选择性信道如何设计异步发射结构没有进行研究。

本文在异步发射思想的驱动下，提出了一种可以应用于莱斯信道的异步多载波分层空时码发射方案。通过在频域上对各发射天线的子载波进行不同移位，形成多载波的异步发射结构；在接收端利用异步发射形成的满秩成型滤波相关矩阵，将LOS分量转化成一种有利于系统性能改善的因素加以利用，实现了V-BLAST类分层空时码在频率选择性莱斯信道下的有效工作。理论分析和仿真结果表明：异步发射结构能够突破接收天线数的限制，利用复杂度较低的线性检测方法可以获得系统的最大可能分集度。

文章其余部分是这样安排的：第2节给出系统的收发信机模型；第3节讨论多载波异步发射结构在莱斯衰落信道下的误码率性能分析；方案的仿真验证将在第4节给出；最后是对全文的总结。

2 系统模型

2.1 发射机模型

考虑一个具有MT个发射天线、MR个接收天线的垂直分层空时编码(V-BLAST)结构，多载波异步发射方案如图1(a)所示。

首先，对数据序列D0进行信道纠错编码，编码后信息D通过串并转换分配到MT个子流上，并分别组成长度为N-1的帧，再经过频域成型函数p(f)处理，得到

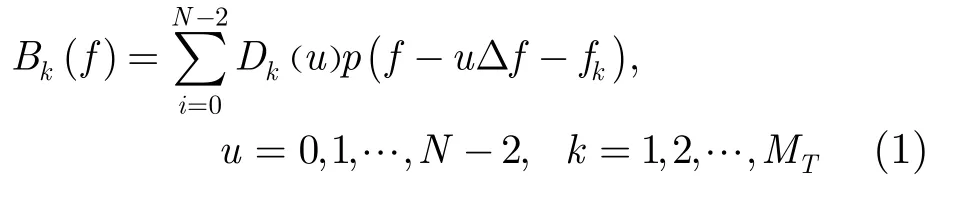
其中Bk(u)表示第k个发射天线上第u个子载波的发射符号；Δf表示子载波间间隔；fk表示第k个天线的频域位移量，这里令0 ≤fk≤Δf，即频域位移量不超过一个子载波间隔；p(f)为频域脉冲成型滤波器函数，为了保证没有成型脉冲带来的能量增益，p(f)满足

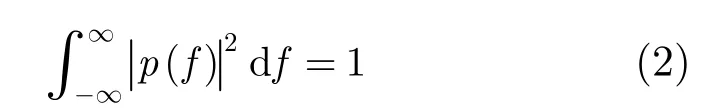
在实际通信系统中这种频域脉冲成型滤波器可以通过数字滤波器加窗，限制带外频谱泄漏的方法来实现，加窗后的频域信号在区间[0 , Δf]外近似为零[10]；对于理论分析，一般假设为矩阵成型脉冲。

经过频域信号移位和补零填充后，发射端各个天线上异步发射符号构成的空频块如图1(b)所示，其中fk+fgk=Δf，在fk和fgk的位置均进行补零操作，保证进行快速傅里叶逆变换(Inverse Fast Fourier Transform, IFFT)的子载波数N是2的整数次幂。

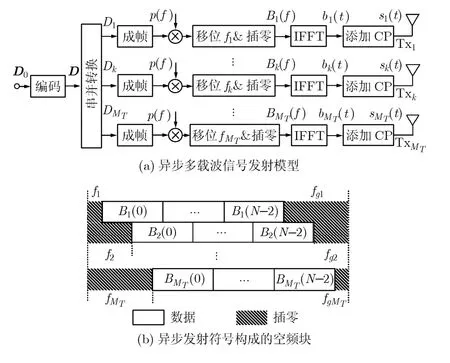
图1 异步多载波信号发射模型

对第k个发射天线的频域异步移位信号进行快速傅立叶逆变换，有

其中F-1{·}表示傅立叶逆变换；Es为总发射能量，每个发射天线分配的发射能量为Es/MT。

经过快速傅立叶逆变换，对各天线信号添加循环前缀 (Cyclic Prefix, CP)后发射，各天线发射信号为sk(t)。

2.2 接收机模型

本文考虑一个独立同分布的莱斯衰落 MIMO(Multiple Input Multiple Output)信道，用hj,k(t;τ)代表第k个发射天线到第j个接收天线间的复衰落系数，采用抽头延时线模型可以表示为[8]

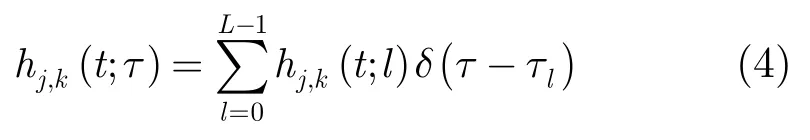
式中δ(·)是狄拉克函数，τl表示第l径的延时；hj,k(t;l)表示第k个发射天线到第j个接收天线的第l径的复增益，可看作含有LOS分量和Rayleigh分量的合成信道，假设在一个符号周期内衰落近似不变，即“准静态信道”[8]。

第j个接收天线上的信号可以写为

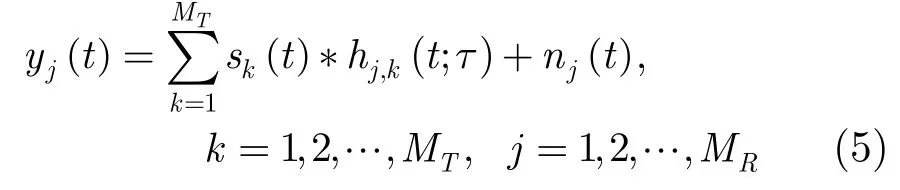
其中A*B表示A与B的卷积；nj(t)表示加性白高斯噪声，均值为0，每一维的方差为=N0/2；且假设各接收天线上的噪声独立同分布。

接收机模型如图2所示：各个接收天线上先进行去CP和快速傅立叶变换(Fast Fourier Transform,FFT)，然后通过匹配滤波器组进行匹配采样，并对采样输出信号进行合并和检测，最后进行相应的译码。

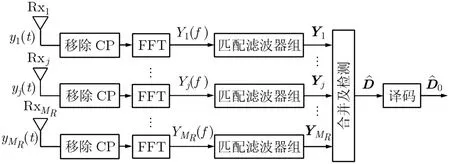
图2 异步多载波信号接收模型

经去CP和FFT变换后，第j个接收天线的频域信号可以表示为

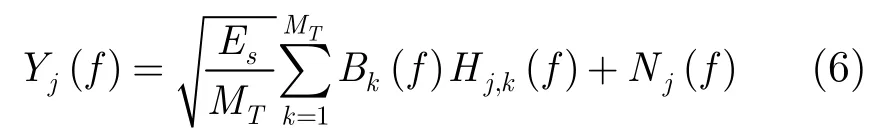
其中Yj(f),Hj,k(f),Nj(f)分别为yj(t),hj,k(t;τ),nj(t)经过 FFT处理后的频域形式；在此，假设循环前缀的长度大于信道的最大时延扩展。

接着，把Yj(f)送入一组匹配滤波器进行匹配滤波并采样，第m个发射天线上第v个子载波的匹配采样信号可写为

其中，频域异步发射的位移量fm是在发射端人为设置的，收发双方均已知。

将式(1)，式(3)代入式(7)，整理得Yjm(v)

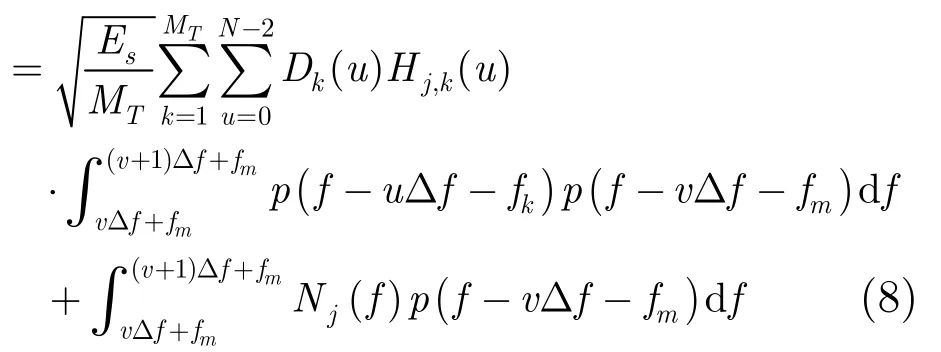
其中Hj,k(u)表示第k个发射天线到第j个接收天线在第u个子载波的信道复衰落系数；v代表接收天线在匹配第m个发射天线各子载波信号时所采用的子载波序号；u代表发射天线k所发射信号的第u个子载波。

为表达简洁，定义：

并进一步定义一个MT×MT的频域波形相关矩阵R(v-u) = {Rmk(v-u)}，由式(9)及发射端p(f)的波形特性可知：

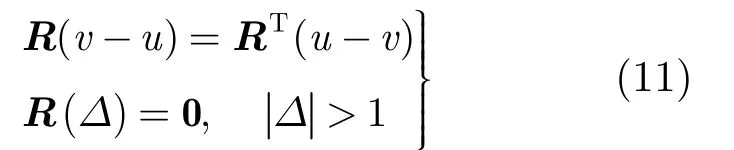
其中 (· )T表示矩阵转置操作。

进而，将第j个接收天线在第u个子载波的频域信道元素组成MT×MT的对角阵：

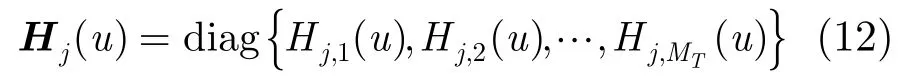
至此，可以将式(8)整理成向量形式：

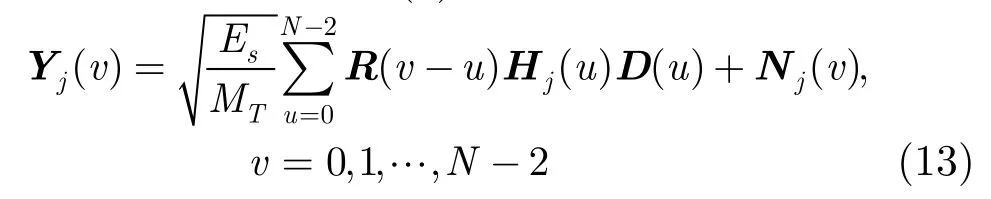
进一步对式(13)整理，得到第j个天线上接收到的所有(N- 1 )MT个采样输出，写成一个(N-1)MT维的向量表达式，即

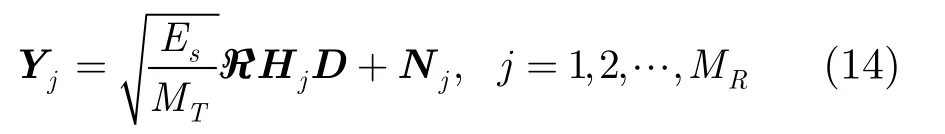
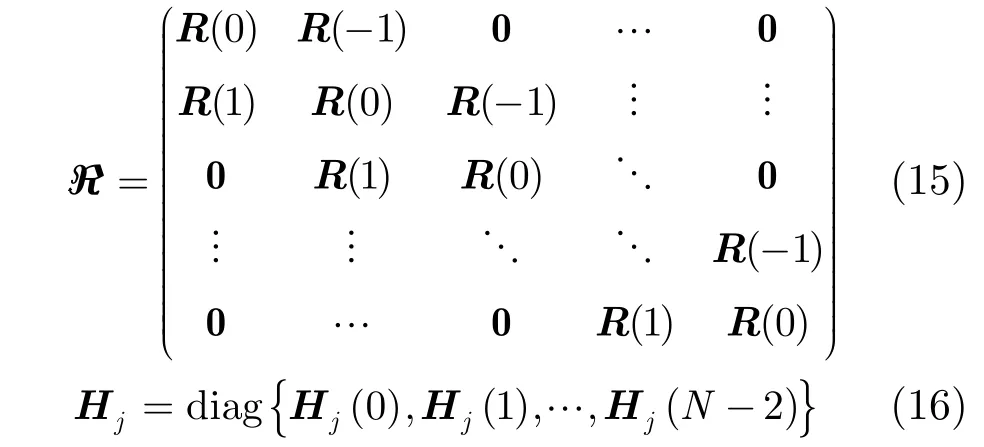
2.3 有关检测的讨论

考察式(14)可知：第j个接收天线上的信号Yj包含了所有MT个发射天线上从0至N-2个子载波的发送信息。经过对各子流信号在频域进行不相等的移位，保证了频域波形相关矩阵ℜ是非奇异的(可逆)[11]，而且信道矩阵Hj又是一个对角线元素非零的对角矩阵，可以通过迫零的方法实现检测：

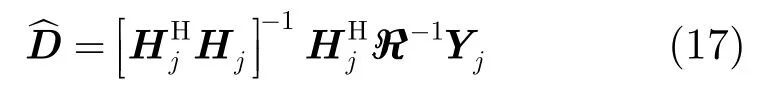
其中 (· )H表示矩阵共轭转置操作；在此，假设接收机已知信道信息。

从式(17)可以看出，利用异步频域位移量的差异性，在保证频域波形相关矩阵ℜ可逆的前提下，频域多载波异步发射方案可以仅仅通过一个接收天线j就可以获得足够的自由度来检测(区分)MT个发射天线上的信号，突破了传统同步多载波V-BLAST对于接收天线数目MR≥MT的限制；若再将多个接收天线的信号适当合并(联合)处理，则可能利用其它接收天线来提供更大的分集增益，对于迫零检测算法，接收端MR个接收天线上接收信号的联合检测可以表达为

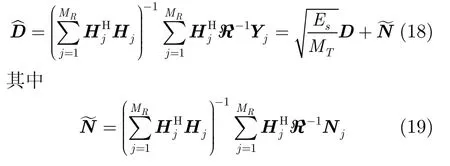
3 性能分析

3.1迫零检测下的性能分析

由式(9)的定义知频域波形相关矩阵具有共轭对称性质，即ℜ-1=ℜ-H，则根据式(19)可计算得到噪声的协方差矩阵为

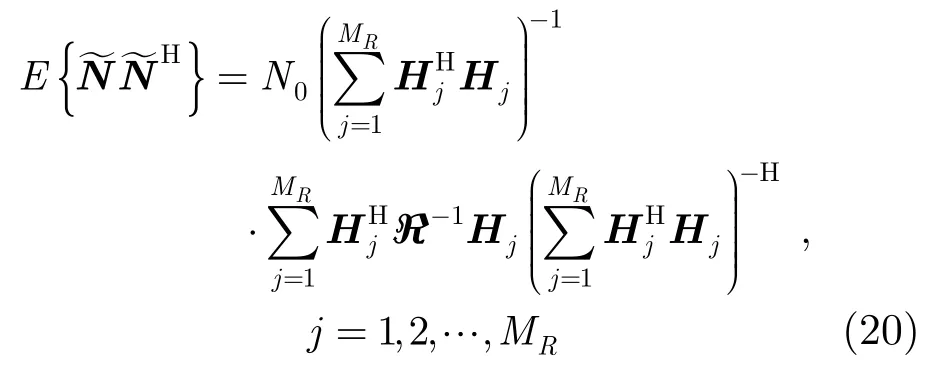
从式(20)我们可以得出第k个子流上第u个子载波符号上的噪声功率为

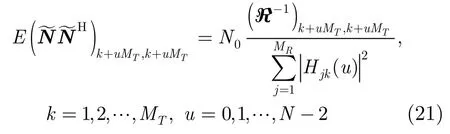
其中(A)i,j代表矩阵A的第i行第j列元素。

那么，第k个子流上第u个子载波符号的瞬时信噪比可表达为

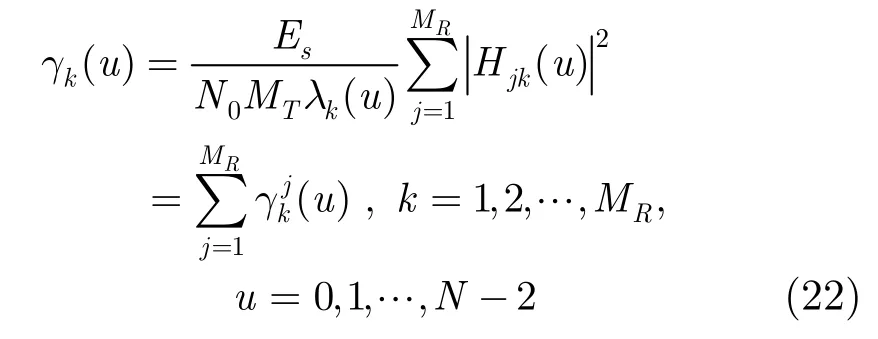
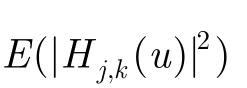
由式(22)，式(23)可知，各接收天线上的平均信噪比(u)与j无关，而瞬时信噪比(u)是与j有关的函数。

为了计算平均符号错误概率(Symbol Error Rate, SER)，首先需要计算信道已知下的条件SER，然后再对信道概率进行积分平均。在信道已知下的条件SER可以表达为[12]

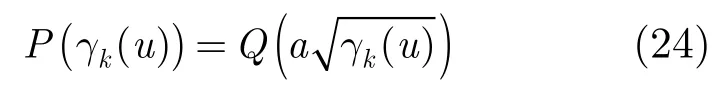
其中a视调制方式而定，在BPSK调制下，a= 2。

对式(24)中的条件SER在信道统计φ(γk(u))意义下求积分平均，得到平均SER为

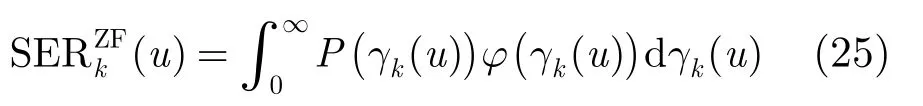
其中，概率密度函数φ(γk(u))为

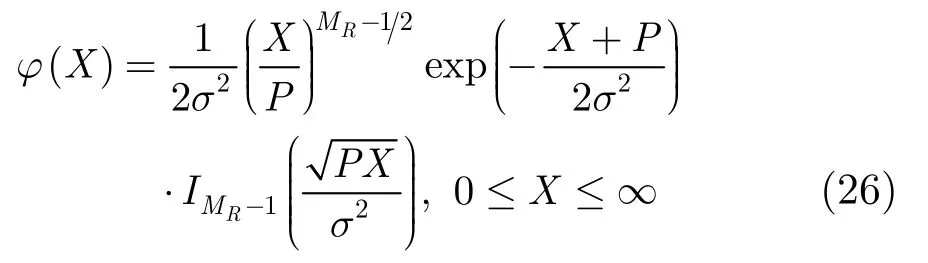
其中In(x)是n阶修正的 Bessel函数； 2σ2=1/(1+K),P=MR K/ (1 +K),K为莱斯K因子，代表LOS分量和Rayleigh散射分量之间的能量比。当采用BPSK调制时，通过积分运算[12]可以得到式(25)的闭合形式误码率表达式：

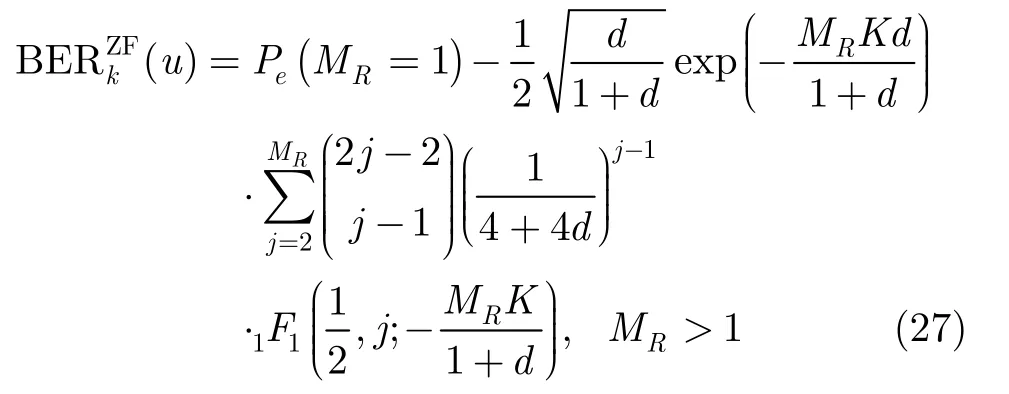
其中Pe(MR= 1 )是当MR= 1时的误码率：

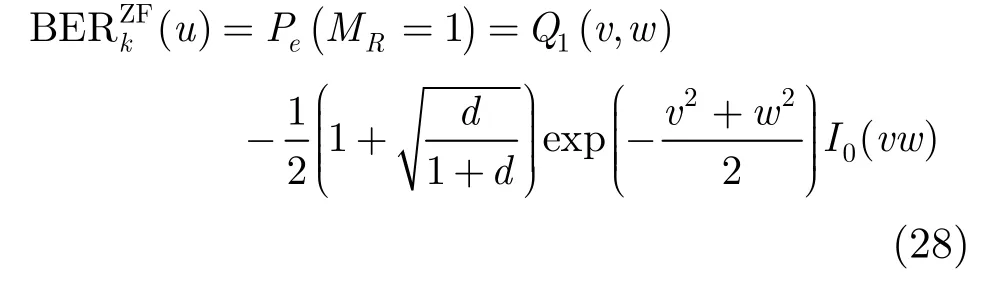
其中Qm(x,y)是广义的Marcum’s Q函数，1F1(x,y;z)代表合流超几何函数(confluent hypergeometric function)。参数d,v,w与调制方式、信道设置相关，在BPSK调制下的表达式分别为

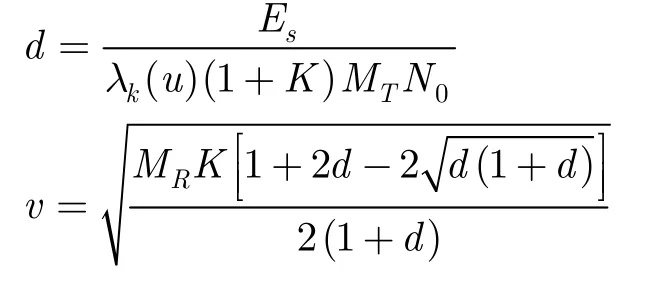
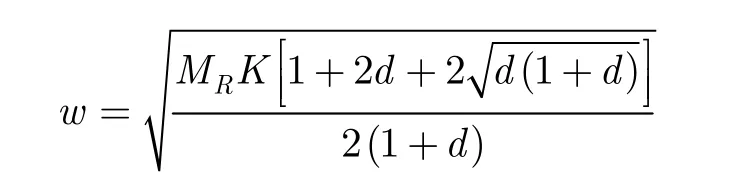
若发射端第u个子载波位置出现±1的概率相等，则第k个子流上的BER为

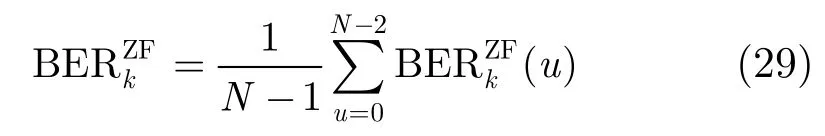
联合迫零检测分集度为

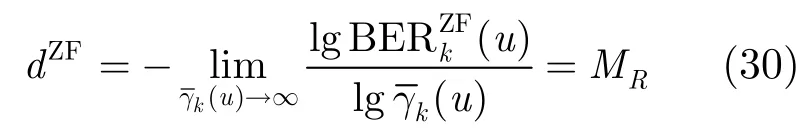
3.2 联合 MMSE检测下的性能分析

由文献[13]可知，虽然系统可以通过迫零的线性方法实现检测，但是迫零并不是最优的线性检测算法，其最优的线性检测算法为多天线联合 MMSE(Minimum Mean Square Error)。

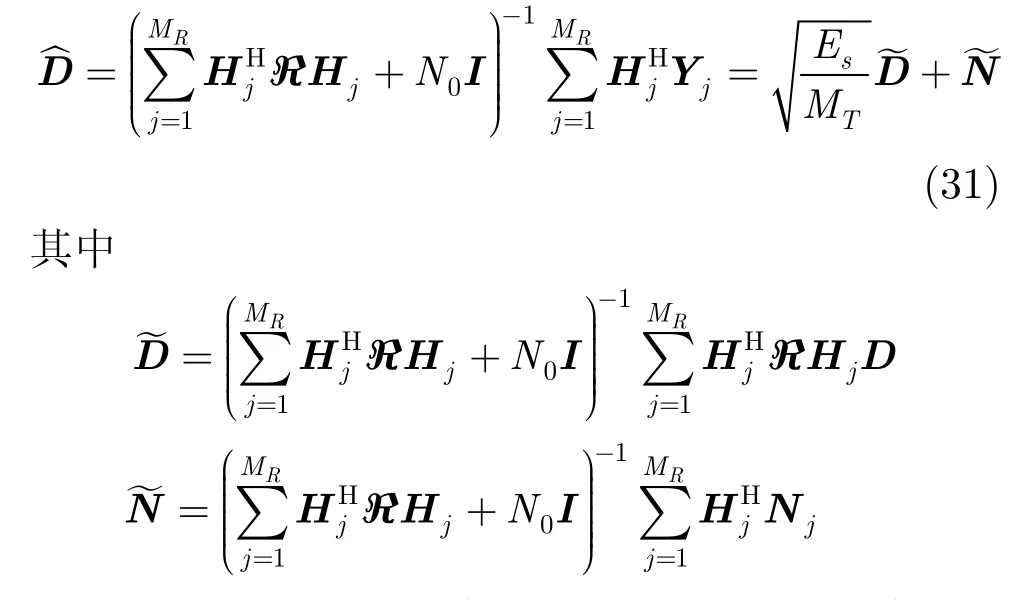
比较联合MMSE检测式(31)和联合迫零检测式(18)，会发现随着信噪比的增加，噪声功率对检测贡献变小，两者检测性能趋于一致；文献[13]分析了时域异步多天线联合MMSE检测的分集度，其结论对式(31)仍然成立，即分集度为MR。

4 计算机仿真结果及分析

为了验证以上理论分析结果的正确性，并进一步与传统同步多载波做对比，本节给出了计算机仿真的结果。在仿真中，采用归一化的独立同分布莱斯衰落MIMO信道，仿真参数如表1所示。

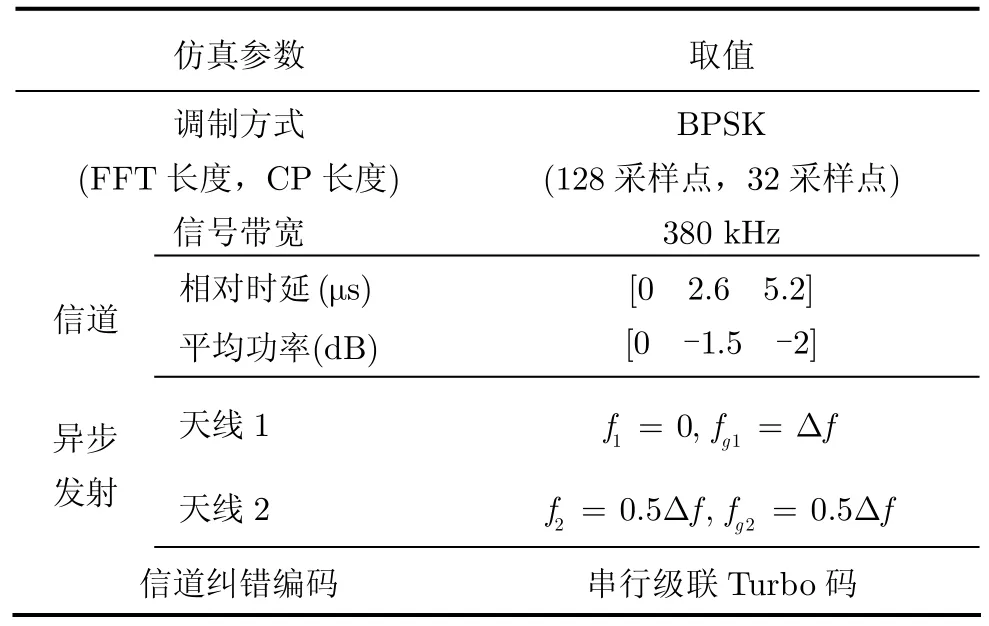
表1 系统仿真参数设置

在异步多载波系统中，由于频率移位和补零操作浪费了一定的频谱效率，为了比较的公平性，异步多载波发射符号能量需要满足：Es=[(N-1)/N]，其中为同步多载波的符号能量。

图3给出了联合ZF检测下异步多载波发射方案误比特率理论分析与仿真的对比曲线。从仿真结果可以看出：(1)异步多载波分层空时码能够利用一个接收天线检测出MT个发射天线上的信号，突破了传统同步多载波 V-BLAST对于接收天线数目MR≥MT的限制[8]；(2)随着莱斯K因子增大，BER性能有所提升，原因在于，采用异步发射结构后，接收信号式(14)中的信道矩阵为对角阵，当LOS分量增加时(K增大)，各对角元素进一步趋于一致，信道矩阵H的条件数得到改善，而同步发射情况由于ℜ矩阵是奇异的，其信道矩阵是满元素矩阵，其条件数随着LOS分量增加而增加，趋近病态，这一点在平坦衰落信道下单载波系统中也得到了验证[9]；(3)在固定发射天线数目的情况下，随着接收天线数的增加，误比特率曲线斜率随之增大(变陡)，从仿真角度验证了异步发射结构线性检测算法的理论分集度分析。

图4给出了2发2收、ZF和多天线联合MMSE检测下异步多载波与同步多载波在Turbo编码和未经编码条件下的误比特率性能比较，其中同步多载波结构相当于异步多载波的各天线频率位移量为0，即图 1中的f1=f2= 0。从图中可以看出，在莱斯信道下，同步系统由于信道相关性导致信道趋于病态(信道矩阵条件数增大)，ZF和MMSE线性检测方法需要较高的信噪比；异步多载波方案，由于子载波异步设计，造成了天线间子载波非正交干扰，ZF检测对单天线处理后简单合并，没有对这一干扰进行抑制，导致性能恶化，而MMSE检测联合了多个天线信号统一处理，对多天线间的子载波干扰具有抑制作用，性能得到了明显的提升。

在实际无线通信应用中，更关心系统误块率(Block Error Ratio, BLER)的性能情况[14]。因此，图5给出了2发2收、多天线联合MMSE检测下异步多载波与同步多载波在Turbo编码和未经编码条件下的误块率性能曲线。从误块率仿真结果看到：莱斯信道下，若不采用信道纠错码，则同步和异步发射都不能达到常规无线高速通信系统的误块率指标需求(一般要求为0.001)[14]；而采用Turbo编码后，异步多载波的性能得到明显改善，在Eb/N0=8.25dB时，误块率达到了0.001；但同步多载波由于其在莱斯信道下MMSE检测算法已经失效，因此信道纠错编码也无法挽回其性能。

图3 莱斯信道ZF检测下异步多载波理论与仿真曲线比较

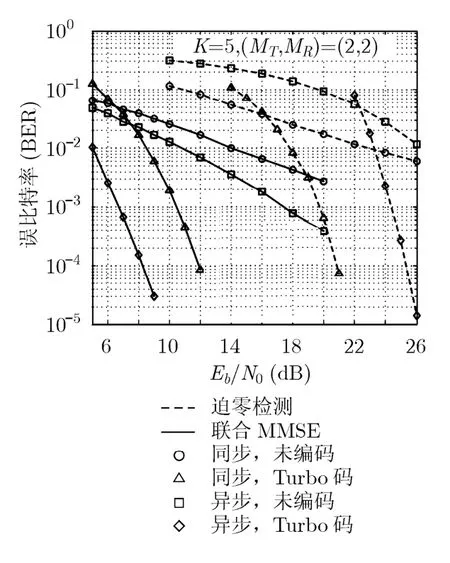
图4 2发2收异步多载波与同 步多载波误比特率对比曲线

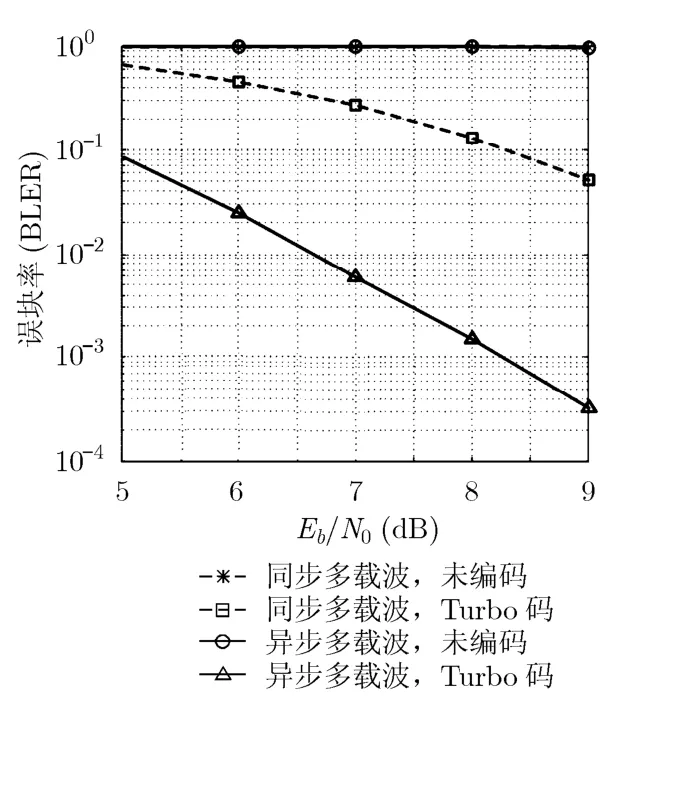
图5 联合MMSE检测下2发2收异步 多载波与同步多载波误块率对比曲线

5 总结

本文给出了一种可以应用于莱斯信道特性的多载波分层空时编码方案，通过频域多载波的异步发射，形成接收端的满秩成型滤波相关矩阵，使得一个接收天线就可以获得信号检测需要的全部自由度，在此基础上联合多个接收天线，实现了该结构下的最大可能分集度。异步发射思想解决了由于近距离接入造成视距信道概率增加而常规同步分层空时码线性检测失效的现实问题。

[1]Ramezani M and Hajiaghayi M. Receive antenna selection for unitary space-time modulation over semi-correlated Ricean channels [J].IEEE Transactions on Communications, 2010,58(2): 521-530.

[2]Artes H, Seethaler D, and Hlawatsch F. Efficient detection algorithms for MIMO channels: a geometrical approach to approximate ML detection[J].IEEE Transactions on Communications, 2003, 51(11): 2808-2820.

[3]Samuel M and Fitz M. Multi-strata codes: space-time block codes with low detection complexity [J].IEEE Transactions on Communications, 2010, 58(4): 1080-1089.

[4]Bαs∂ r E, Ayg˙olu˙ U , Panayirci E,et al.. Space-time block coded spatial modulation[J].IEEE Transactions on Communications, 2011, 59(3): 823-832.

[5]Gesbert D. Robust linear MIMO receivers: a minimum error-rate approach [J].IEEE Transactions on Signal Processing, 2003, 51(11): 2863-2871.

[6]Akhtar J, Gesbert D, and Hjorungnes A. Linear closed-form precoding of MIMO multiplexing systems in the presence of transmit correlation and Ricean channel [C]. Proc. IEEE Global Telecommunications Conference (Globecom), Dallas Texas, USA, 2004: 3160-3164.

[7]Wang Qi-xing, Chang Yong-yu, and Yang Da-cheng.Deliberately designed asynchronous transmission scheme for MIMO systems [J].IEEE Signal Processing Letters, 2007,14(12): 920-923.

[8]Paulraj A, Nabar R, and Gore D. Introduction to Space-Time Wireless Communications[M]. Cambridge: UK, Cambridge Univ. Press, 2003: 152-155.

[9]Shao Shi-hai, Tang You-xi, and Ma Wan-zhi. Layered spacetime codes over Ricean fading channels by reducing the correlation of spatial shaping pulses [J].IEEE Transactions on Wireless Communications, 2009, 8(2): 574-579.

[10]Ochiai H. Exact and approximate distributions of instantaneous power for pulse-shaped single-carrier signals [J].IEEE Transactions on Wireless Communications, 2011, 10(2):682-692.

[11]Verdu S. Multiuser Detection [M]. Cambridge: UK,Cambridge Univ. Press, 1998: 166-175.

[12]Lindsey W C. Error probabilities for Rician fading multichannel reception of binary and N-ary signals [J].IEEE Transactions on Information Theory, 1964, 10(4): 339-350.

[13]易新平, 唐友喜, 邵士海, 等. 分布式发射天线MIMO信号的最优线性检测[J]. 电子学报, 2009, 37(12): 2694-2699.

Yi Xin-ping, Tang You-xi, Shao Shi-hai,et al.. Optimal linear detection algorithm of MIMO with distributed transmit antennas[J].Acta Electronica Sinica, 2009, 37(12):2694-2699.

[14]3GPP. TS. 25.141 v9.4.0. Base Station (BS) conformance testing (FDD). 2010.06.21.