多小区OFDMA解码转发中继通信系统的分布式资源分配算法

陈瑾平 何世文 杨绿溪

(东南大学信息科学与工程学院 南京 210096)

1 引言

现有的关于OFDMA系统动态资源分配问题的研究主要集中在单小区环境而不考虑共信道干扰。文献[1]研究了多载波系统固有的渐进强对偶性，并给出严谨的理论证明和对偶间隙的误差估计。基于该结论，根据单小区OFDMA系统下的不同场景，往往可以联合优化各种无线资源，得到多项式时间复杂度的近似最优的资源分配算法[2,3]。

然而，实际的无线通信系统是干扰受限的多小区蜂窝网络，为了提高系统的频谱效率而采用全频率复用方式。所以，小区间干扰成为影响系统性能的关键因素之一。对于多小区系统来说，基于对偶求解的联合资源优化仅具有理论上的意义。

多小区系统的资源分配为满足实时性要求往往采用分步方法：基站之间的协调调度和功率优化。合理的用户调度、子载波分配以及功率优化对系统性能的提升起着关键的作用[4]。基于干扰协调的子载波分配往往需要反馈大量的信道信息，需要极大的系统开销[5]。多小区环境下的功率控制由于数学形式的非凸性使得优化问题更为复杂，多用户迭代注水算法通过将其它小区的干扰作为噪声反复迭代往往达不到较好的局部最优性能[6]；文献[7]对迭代注水算法进行修正，从而得到更优的性能，但该算法的收敛性无法保证。

多小区OFDMA系统引入中继节点后，增加了中继选择、以及时分双工两个时隙频谱分配的自由度，更增加了资源分配问题的复杂性[8]。

现有的关于多小区中继系统资源分配的工作还很少。文献[9]考虑了上行链路多小区系统，侧重于设计一个复杂度较低的算法，没有考虑功率的优化，与传统的不考虑干扰情形算法相比，性能有一定提高。文献[10]针对下行链路系统，不考虑相邻小区基站对中继的干扰影响。算法可以看作是文献[1]的结论在多小区系统下的应用，通过引入一个干扰的阈值常量，将中继OFDMA系统中资源分配简化为一个凸问题求解。然而，该阈值常量如何确定是问题的关键所在，性能较好的小区参数需要从统计的概率上去选取，而且该文的场景只适合大半径蜂窝小区的情形，新一代无线通信系统中为进一步提高频谱效率，在较小的小区半径场景下，不得不考虑中继以及用户所受到的共信道干扰。

本文针对多小区OFDMA解码转发中继通信系统的资源分配，考虑小区中继端以及用户接收端都受到相邻小区的干扰。此类混合离散型问题是NP-hard的，最优的求解极其困难。本文采用分布式资源分配算法，各小区之间不需要交换系统信息，独立地完成用户调度和载波分配，资源分配策略大大减少了信道状态信息(CSI)的反馈开销；小区根据调度结果，分布式进行功率控制，小区之间信息交换只需要很少量的系统开销，从而降低了集中式功率优化的复杂度。仿真结果表明，本文算法很大程度地提升了整个系统的吞吐量，并保证了小区内不同区域用户的QoS性能。

2 多小区OFDMA中继通信的系统模型

考虑采用全频率复用的中继协同通信多小区OFDMA系统，系统带宽为B，分成N个子载波。系统内有L个小区，小区l内分布个中继，以连接基站与中继用户之间的通信链路。基站与中继具有各自独立的功率约束，分别为小区内用户分为两类：直传用户m∈Dl或中继用户m∈Rl。系统采用TDD半双工解码转发中继，第1时隙，基站向中继和直传用户发送数据；第2时隙，中继将接收到的信息发送给中继用户，中继用户不考虑分集接收。假设每个中继用户只能接收一个中继转发的信息，中继与用户之间的这种对应关系根据长期信道状态信息相互确定[11](本文后面的内容不再注明这种对应关系)。用户的数据队列始终是“全缓冲”状态。信道状态信息相对于调度时间具有慢时变性。

首先需要确定用户的直传模式或中继模式，采用一个简单实用的标准对小区用户类型进行划分：

对于直传用户m∈Dl，在第1时隙，基站l通过子载波n向m发送数据。

式(2)中第2项为相邻小区l′对m的共信道干扰项，且有

对于中继用户m∈Rl，第 1时隙，基站l首先经子载波n向与m对应的中继k发送数据。

第2时隙，中继k经子载波向中继用户m传送数据。

至此，可以写出基站l至直传用户m∈Dl链路上子载波n信道的容量表达式：

基站l经中继k至中继用户m∈Rl链路上子载波对(n,)信道的容量表达式：

3 系统模型下资源分配问题的数学描述

本文中，多小区OFDMA 中继通信系统动态资源分配的目标是：在满足基站、中继功率约束和保证各用户通信服务质量(QoS)要求的前提下，通过合理的用户调度和资源分配，使得系统吞吐量达到最大。

所以，该优化问题的目标函数可描述如下：

其中Ω(m),m∈Dl∪Rl表示分配给用户m的第1时隙子载波集合。

因为在一个小区内的任何一个时隙中，每一条子载波只能被一条链路占用，所以有式(8)的约束条件：

OFDMA系统下的用户通信服务质量性能可以通过不同的指标实现，在单小区环境下，严格的速率要求往往可以得到近似最优的满足[3]；但在多小区环境下，共信道干扰使得小区之间的资源分配相互交织在一起，本文参照文献[6]，给每个用户分配尽可能相等的子载波，分配约束如式(9)：

功率分配须满足基站和中继的功率约束，分别表述如式(10)：

约束条件式(8)-式(10)和目标函数式(7)构成一个混合离散型的优化问题，属于NP-hard问题，穷举搜索的情形下，可能的子载波分配是N的指数级，而且每种载波分配下的功率控制也是一个非凸的优化问题。

4 分布式资源分配算法

本文提出次优的资源优化算法，首先分配子载波给小区内各个用户，然后基于调度结果进行功率分配。

4.1子载波分配策略

对于多小区OFDMA中继通信系统，信道状态信息的反馈既包括反馈本小区内信道的 CSI，也包括反馈相邻干扰信道的 CSI。如果减少反馈节点的数量，则可以大大降低反馈信道信息所需要的系统开销。

每个小区内分布式进行子载波分配，不需要与其它小区交换子载波分配的信息。对于某个小区内的直传用户和解码转发中继来说，第1时隙的信道质量是容易确定的，这是因为干扰源容易确定(即相邻的每一个基站)；对于中继用户来说，第2时隙内的干扰源难以确定(干扰可能来自其它小区内的任何一个中继，也可能其它小区第2时隙并没有占用这个信道)。

解码转发中继信道容量取决于两跳信道中信道质量相对较差的一跳。直观上，对于干扰严重的场景下，接收节点的信干噪比可以通过它与两个干扰源的相对距离定性反映(大尺度衰落)。第 1时隙的信道分配则显得更为重要，这是因为第2时隙并没有占用所有的子载波资源，其次相邻小区即使存在共信道干扰，同一条子载波也未必会分配给最接近的两个中继。

子载波分配策略分成以下3步：

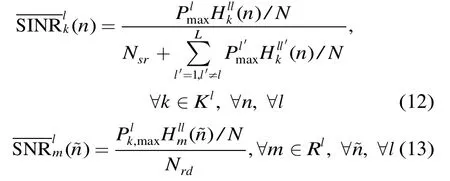
(2)然后，基于以上的反馈信息，小区l进行用户调度和子载波的分配。

对于尚未分配的第1时隙的子载波n∈，选择用户m*使得

(3)反馈调度好的用户所分配子载波的干扰信道CSI。

由以上过程可知，本文子载波分配算法中需要反馈的信道信息只是全反馈信道信息下的1/L，大大降低了系统的反馈开销。

4.2 功率控制策略

多小区场景下的功率控制问题是非凸的优化问题，直接求解无法满足资源分配的实时性要求。与无中继OFDMA多小区系统相比，中继节点的接入，使得小区内满足高信干噪比条件的区域进一步增大，也是本文功率控制问题简化的依据。

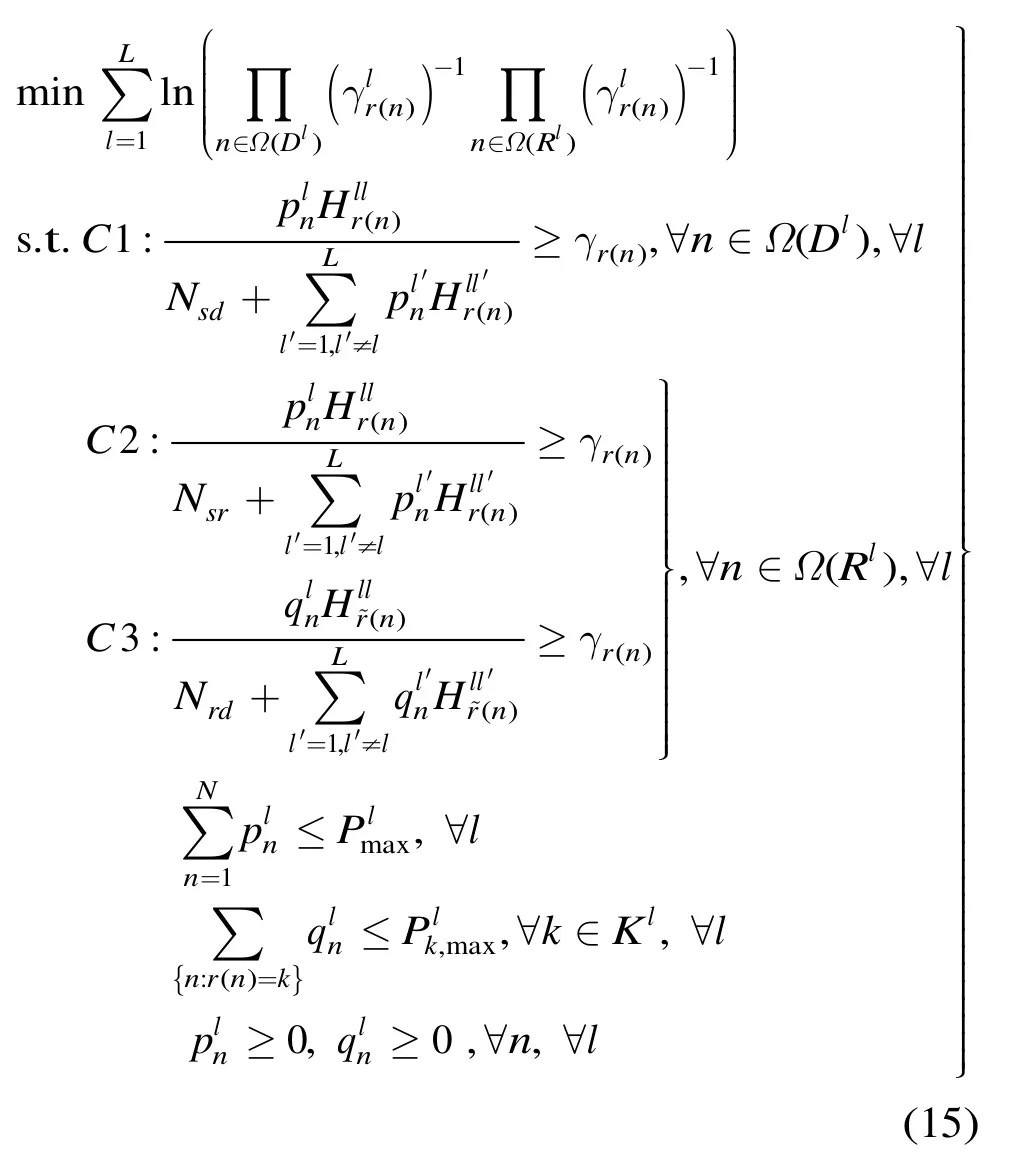
式(15)无论是目标函数还是约束函数都是正项式，是几何规划问题(GP)的正项式形式。

虽然功率优化问题在高信干噪比下简化为 GP问题，然而GP问题求解的复杂度随优化变量数目和约束条件数目的增加呈非线性快速增长关系[12]，小区之间的共信道干扰使得直接求解功率优化问题式(15)复杂度仍然较高。本文提出分布式的功率控制方法，将式(15)分解为L个子问题求解，即每个小区基于局部变量和局部约束条件进行功率分配，从而进一步简化原问题的求解。

则可以得到下面与式(15)等价的优化问题：

对式(17)的约束条件C1,C2和C3进行对数变换，并代入相应的辅助变量。由此，可得到式(17)的部分拉格朗日函数(不含功率项约束)：

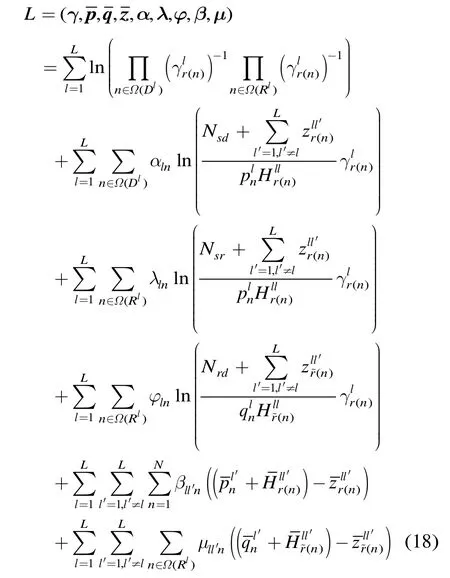
注意：拉格朗日函数式(18)中等式右边的第2, 3,4项并没有替换为相应的辅助变量，是为了表述清晰，避免公式过于繁冗，但这样的书写方式并不影响对于公式推导过程的理解；同理，下面各式依样处理。

式(18)的对偶函数严格地表述如下：

进一步分析部分拉格朗日函数式(18)，并对相应的各个小区的局部变量(包括辅助变量)进行分离，得到

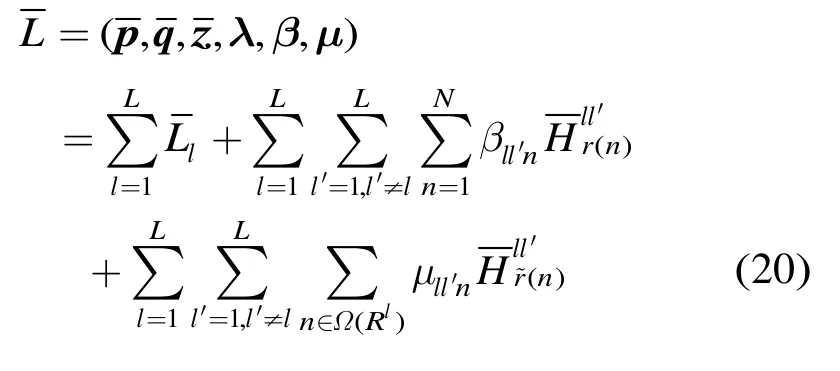
至此，有以上各步的推导，可以得到功率控制问题式(17)的对偶问题为

由 Slater条件[13]可知，问题式(17)与对偶问题式(22)满足强对偶性，即对偶间隙等于零，所以求解对偶问题式(22)可以得到功率约束问题式(17)的最优解。

式(23)对应着每个小区基于局部变量分布式进行功率控制。对于给定的(λ,β,μ)，目标函数是凸函数，约束条件是凸集，显然每个小区内的功率优化子问题是凸优化问题，本文不再赘述其具体的求解过程。

下面讨论对偶问题的求解。式(22)中除了非负的对偶变量约束C1，还有不等式约束C2存在，传统的次梯度算法不再适用，本文采用收敛更快、收敛速度可保证的椭球算法求解。椭球算法中每次椭球体的迭代收敛过程运算开销较大的只是两次矩阵与向量的乘积，所以可以设置一个小型的中心控制器完成迭代，也可以由各个小区根据交换的局部功率控制最优解独立完成。对于整个小区系统来说，基站之间有线链路可以提供强大的数据传输能力，足够快速地在各个小区间传递所需要的信息，各个基站根据更新后的(λ,β,μ)分布式进行功率控制。椭球算法的这种开销是值得的，因为椭球体迭代收敛次数更少，则基站分布式功率优化的次数也更少，整体系统开销更小。

对于本文的椭球算法，下面给出椭球体迭代收敛过程中必要的参数，省略相关参数具体的求解过程。

(1)收敛梯度：

(a)当椭球体中心不满足约束条件C1时，∇=em；

(b)当椭球体中心不满足约束条件C2时，∇=-em；

在(a), (b)中，m为[λ,β,μ]T中任一不满足条件的变量序号，em为第m个变量为1的单位向量。

(c)当约束条件C1,C2都满足时，∇=[∇λ,∇β,∇μ]T

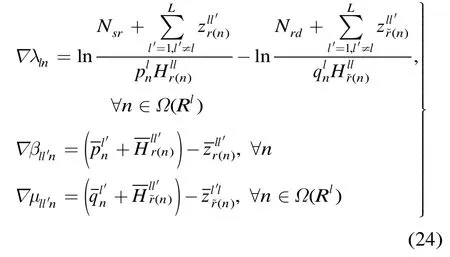
可以得到对偶变量的取值范围：

由式(25)可以确定算法的初始椭球体。

本文进一步给出下列结论，以减少优化变量简化优化问题式(17)的求解：

(1)邻近小区的干扰是主要干扰源，忽略来自较远小区的干扰项并不会影响功率控制的性能；

(2)由均值不等式容易证明：对于简化的功率控制问题式(17)，同一小区内的基站至直传用户链路上的所有载波功率优化后的最优解是相等的。

5 仿真结果及分析

图1比较了算法在不同半径小区系统下的平均吞吐量性能。仿真给出了在资源分配过程中不考虑小区之间共信道干扰的最优的 NCO(No COordination)算法以及中继场景下文献[6]的追求系统容量最大化的CO(COordination)算法。从仿真结果可以看出，本文算法的吞吐量性能都有非常大的增益。这是因为在小半径情形下，小区之间的共信道干扰功率比之高斯噪声功率大得多，相比NCO算法不考虑干扰以及CO算法干扰常量化迭代功率优化，本文算法同时考虑了邻近基站对直传用户以及中继端的干扰，也考虑了邻近中继对中继用户的干扰。随着小区半径的减少，小区间干扰更加强烈，本文所提出的多小区资源分配算法对干扰的抑制作用相比有更加明显优势。

图2比较了小区半径700 m系统下中心小区内不同区域用户的吞吐量性能，反映了通信服务质量的好坏。仿真中，由近至远绕基站将小区分为5个等面积的“环状”区域(当然因为小区是正六边形的，所以不可能是真正的圆环状)，每个区域内用户分布的数目概率相等。从图2可知，本文所提算法与不考虑干扰情形下 NCO算法相比，无论是中心用户和边缘用户的吞吐量性能都有很大的提升。

图1 不同小区半径下的系统平均吞吐量性能比较

图2 小区内不同区域用户的吞吐量性能比较

6 结束语

本文研究了多小区OFDMA中继通信系统中的动态资源分配问题，为了保证用户通信质量，提出了公平性载波分配下的次优的分布式资源分配算法。算法充分考虑了小区之间较强的共信道干扰的影响，与传统的几种算法相比，大大提升了整个系统的吞吐量性能，而且对于小区内不同区域用户能提供更好的QoS保证。所设计的算法，减少了信道状态信息反馈的系统开销；功率控制过程简化为凸优化问题，是多项式时间算法，并通过分布式设计进一步加快了收敛的速度，能满足系统资源分配的实时性要求。

[1]Luo Z Q and Zhang S Z. Duality gap estimation and polynomial time approximation for optimal spectrum management.IEEE Transactions on Signal Processing, 2009,57(7): 2675-2689.

[2]Kim B G and Lee J W. Joint opportunistic subchannel and power scheduling for relay-based OFDMA networks with scheduling at relay stations.IEEE Transactions on Vehicular Technology, 2010, 59(5): 2138-2148.

[3]Zhang D H, Wang Y Z, and Lu J H. QoS aware resource allocation in cooperative OFDMA systems with service differentiation. IEEE International Conference on Communications, CapeTown, South Africa, May 2010: 1-5.

[4]Venturino L, Prasad N, and Wang X D. Coordinated scheduling and power allocation in downlink multicell OFDMA networks.IEEE Transactions on Vehicular Technology, 2009, 58(5): 2835-2848.

[5]Rahman M and Yanikomeroglu H. Enhancing cell-edge performance: a downlink dynamic interference avoidance scheme with inter-cell coordination.IEEE Transactions on Wireless Communications, 2010, 9(4): 1414-1425.

[6]Pischella M and Belfiore J C. Power control in distributed cooperative OFDMA cellular networks.IEEE Transactions on Wireless Communications, 2008, 7(5): 1900-1906.

[7]Yu W, Kwon T, and Shin C Y. Joint scheduling and dynamic power spectrum optimization for wireless multicell networks.Conference on Information Science and Systems (CISS),Princeton, NJ, March. 2010: 1-6.

[8]Salen M, Adinoyi A, Yanikomeroglu H,et al.. Opportunities and challenges in OFDMA-based cellular relay networks: a radio resource management perspective.IEEE Transactions on Vehicular Technology, 2010, 59(5): 2496-2510.

[9]Odeh N, Abolhasan M, and Safaei F. Low complexity interference aware distributed resource allocation for multi-cell OFDMA cooperative relay networks. IEEE Wireless Communications and Networking Conference,Sydney, Australia, April. 2010: 1-6.

[10]Ng D W K and Schober R. Resource allocation and scheduling in multi-cell OFDMA decode-and-forward relaying networks.IEEE Transactions on Wireless Communications, 2011, 10(7): 2246-2258.

[11]Bletsas A, Khisti A, Reed D P,et al..A simple cooperative Diversity Method Based on network path selection.IEEE Journal on Selected Topics in Communications, 2006, 24(3):659-672.

[12]Kortanek K O, Xu X, and Ye Y. An infeasible interior-point algorithm for solving primal and dual geometric programs.Matematical Programming, 1997, 76(1): 155-181.

[13]Boyd S and Vandenberghe L. Convex Optimization.Cambridge, Britain: Cambridge University Press, 2004:215-273.