海面漂浮小目标的特征联合检测算法

时艳玲 水鹏朗

(西安电子科技大学雷达信号处理国防重点实验室 西安 710071)

1 引言

检测海面的漂浮小目标，例如冰山、浮标、潜望镜等是舰载监视雷达的任务之一，它对海上护航、搜救、港口反恐、航海安全等有重要的指导意义，然而它受到海杂波的干扰。海杂波与雷达载频、掠射角、极化方式、海况、长波的波高、涌浪的波高等因素有关，具有空时非平稳特性[1]。海面漂浮目标随海浪的运动而运动，目标与背景杂波的频谱混叠在一起，导致多普勒域杂波抑制方法[2]失效。在高距离分辨海杂波背景下，由于海浪的运动，漂浮目标使得周围海表面的散射特性发生了改变，目标所在分辨单元的接收回波服从非加性观测模型，建立在加性模型基础上的能量检测算法[3]将失效。

针对上述问题，众多学者基于实测的海杂波和目标数据利用特征差异来检测海面漂浮小目标，主要有基于加性模型和基于非加性模型两类特征检测算法。基于加性模型的特征检测算法有非线性预测方法[4]，它让杂波样本训练出尽可能准确的神经网络，利用预测误差实现目标检测。基于非加性模型的特征检测算法有基于分形方法[5,6]和多普勒谱特征方法[7]等。基于分形方法[5]将海杂波视为随机分形噪声，从时间序列的幅度中提取分形几何特征[5,6]进行海上目标检测，这类方法不仅丢失了时间序列的相位信息，而且要求时间序列的长度为秒级，不能满足雷达工作在扫描模式的时间要求。多普勒谱特征方法[7]使用联合瑞利分布模型描述海杂波的多普勒统计特性，采用波形熵特征表征多普勒谱的扩展程度，该算法只使用了单个特征，它区分杂波和目标的能力有限。在文献[5-7]中，作者没有明确指出非加性模型，它们只是非加性模型的雏形。

本文首先给出非加性模型的解析表达式，然后借鉴文献[8]中将检测问题等价为分类问题的思想，即将目标是否存在等价为接收回波是否属于杂波所在的类，提出了一种基于非加性模型的特征联合检测算法。该算法首先从接收回波中提取平均功率和多普勒谱熵这两个特征，组成一个两维特征向量，对该特征向量进行零均值去相关的归一化处理后对应特征平面上的一个点ξ，然后利用凸包训练算法得到判别区域，最后以点ξ是否包含在判别区域内作为判别准则。该算法无须对杂波和目标建模，不受雷达工作模式的限制。实测的IPIX雷达数据验证了本文算法的有效性，当雷达的距离分辨率为3 m, 9 m, 15 m时，本文算法优于对比算法。

2 非加性回波模型和特征提取

2.1 本文提出的非加性回波模型

海杂波源自入射电磁波和海表面的相互作用，它的特性同许多因素有关[1]。海面后向散射系数对微波雷达照射区域的微细结构很敏感，雷达分辨率越高，这种敏感的表征越明显。漂浮目标影响了周围海面的微细结构，来自目标所在分辨单元的后向散射回波不得不刻画为目标回波s(n)，受影响区域回波cs(n)和正常区域回波αc(n)三者的叠加，其中正常区域是指一个分辨单元中与周围未受目标影响的海面相似的区域。3种回波叠加的模型在本文中被称为非加性模型，即

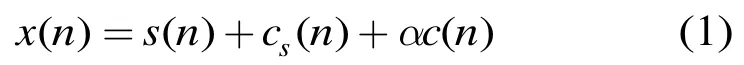
以区别于低分辨下的加性模型x(n) =s(n) +c(n)，其中，x(n)为雷达某分辨单元的接收回波，c(n)为海杂波，n为脉冲数，α=Anormal/A,0 ≤α≤ 1 ,A是雷达分辨单元的面积，A=Anormal+As+Ainfective，如图1所示，Anormal是一个分辨单元中正常海面区域的面积，As为目标面积，Ainfective为一个分辨单元中受影响的海面区域的面积，由于海水的运动，一般Ainfective＞As,Ainfective与目标的尺寸和海况等因素有关的，目标的尺寸越大、海浪越高，Ainfective就越大。一旦目标给定，As即为定值，Ainfective就只与海况有关。

目标检测采用二元假设检验

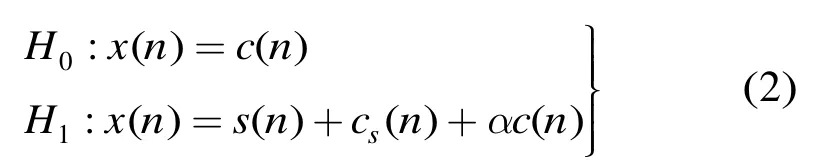
在H0假设下，A=Anormal。在H1假设下，当微波雷达分辨率较低时，若存在目标，如图1(a)所示，Anormal接近A,α≈1,cs(n)可以忽略，本文提出的非加性模型退化为加性模型，目标的统计特性与杂波的统计特性可分开处理，目前众多检测器[2,3]都是基于加性模型设计的。当微波雷达分辨率较高时，若存在目标，如图1(b)所示，Anormal≪A,α≪1，随着分辨率的进一步提高，αc(n)最终将消失，cs(n)成为主要的海杂波，回波模型为非加性模型。

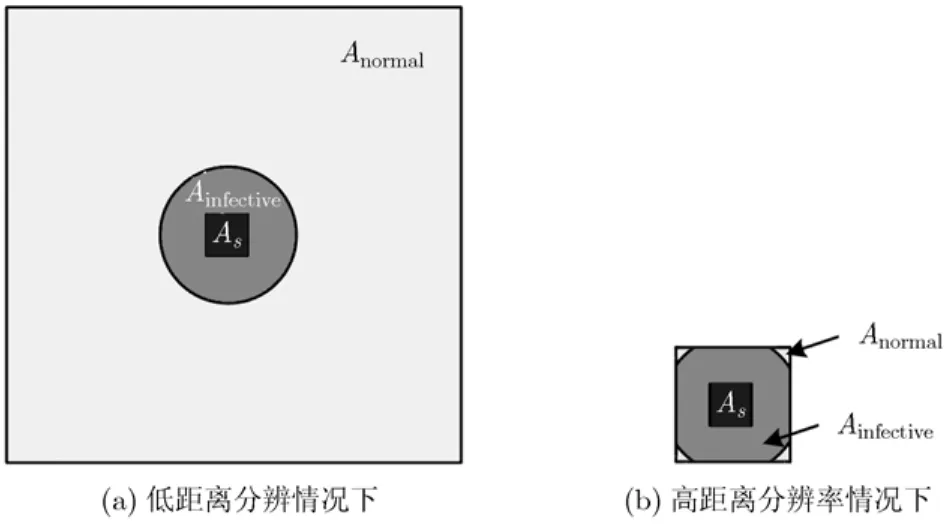
图1 一个距离单元的面积示意图

由于cs(n)是依赖目标而存在的，一旦目标类型或者海况发生变化，cs(n)的统计特性就会随之发生变化，故不能利用邻近单元的海杂波来估计cs(n)的统计特性。另外，来自某个距离单元的回波是这个单元的众多散射子叠加而成的，Ainfective和Anormal无法定量计算，参数α也难以得到。为了避开对参数α的估计和对cs(n)的建模，借鉴文献[8]中将检测问题转化为分类问题的思想，我们也将非加性模型的检测问题式(2)转化为分类问题，即只需确定纯海杂波所属于的类ω，而不需要确定目标所属于的类，目标检测就是判断x(n)是否属于ω。纯海杂波是指从如下的距离单元接收的海杂波，即除了目标所在的单元和受目标影响的单元之外的单元。由于ω只与纯海杂波有关，不涉及α和cs(n)，故而避开了对参数α的估计和对cs(n)的建模。式(2)隐含着若x(n)不是纯海杂波则必然含有目标这个事实，故如果x(n)不属于ω，则x(n)中必然含有目标，则本文的分类问题可表示为

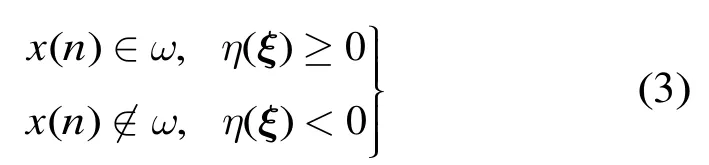
其中ξ为从x(n)中提取的特征组成的向量，对应特征空间的一个点，η(ξ)是关于ξ的标量函数，称为判别函数。上述分类问题是一个异常检测[9]问题：将接收回波映射到特征空间，在这个空间构造最优分类线Ω作为分类器，利用分类器对x(n)进行分类，则式(3)可以转化为

其中Ω为从纯海杂波数据中提取的特征样本构成的分类线，称为判别区域。此时式(2)的检测问题等价为判断点ξ是否在Ω外面的分类问题了。

2.2 特征提取

基于式(4)的分类问题，我们需要提取x(n)的特征。下面介绍两个常用的特征：平均功率和多普勒谱熵[7]。

定义x=[x( 1),x( 2),… ,x(N)]为接收的N个相干脉冲组成的复时间序列，它的平均功率为

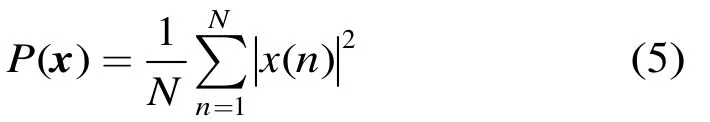
平均功率等效为多普勒谱的零阶距。多普勒谱熵[7]为

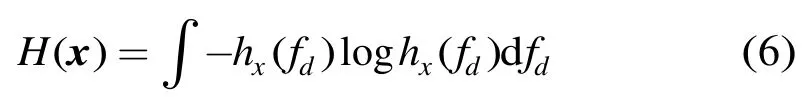
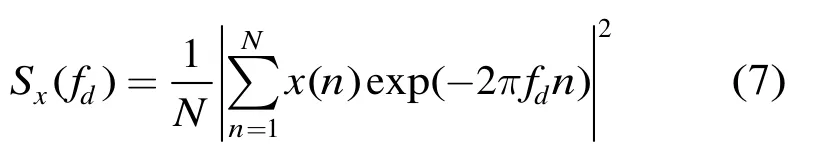
海杂波的平均功率P是被海表面的大尺度波和涌浪的尖峰分量调制的[1]，漂浮目标的存在改变了雷达照射单元海杂波的微细结构，使得纯海杂波的平均功率不同于受目标影响的海杂波平均功率；多普勒谱熵H反映了多普勒谱的扩展程度，由于目标所在单元的回波为3个分量叠加而成的，导致多普勒谱展宽，使得多普勒谱的扩展较大，而纯杂波单元的回波的多普勒谱较为集中，使得多普勒谱的扩展较小。P和H这两个特征刻画了海杂波时间序列在多普勒域的差异，这种差异可以用来判断目标是否存在。这两个特征均不受雷达工作模式(驻留或者扫描)的限制。当然，也可以用其它的特征(诸如分形维数、多普勒偏移、多普勒带宽、归一化多普勒谱的高阶矩等)替换本文提出的特征。

考虑到海杂波的非平稳特性，积累时间应小于纹理分量的相关时间[1]，即 1000N＜ 。笔者已经分析出，单个特征不能获得满意的检测性能，并在实验中解释了原因。故而，在提取了特征后，下文给出了基于两个特征的特征联合检测算法。

3 本文提出的特征联合检测算法

本节提出了基于非加性模型的特征联合检测算法来检测高分辨海杂波背景下的漂浮小目标。为了清晰起见，给出本文算法的原理框图，如图2所示。首先提取海杂波的特征，并进行零均值去相关的归一化处理，然后利用凸包训练算法确定判别区域Ω，再对接收时间序列的特征进行归一化处理，对应点ξ，最后以该点ξ是否在Ω里面作为判别准则。基于式(4)的分类问题，我们需要确定ξ和Ω以及二者的包含关系这3个问题，它们分别对应归一化特征向量、确定判别区域Ω以及判别准则这3步，下面将详细介绍这3步，并在本节最后分析了计算复杂度，给出了样本选择应该注意的问题。

3.1 归一化特征向量

设y是由两个特征分量组合而成的2×1维向量

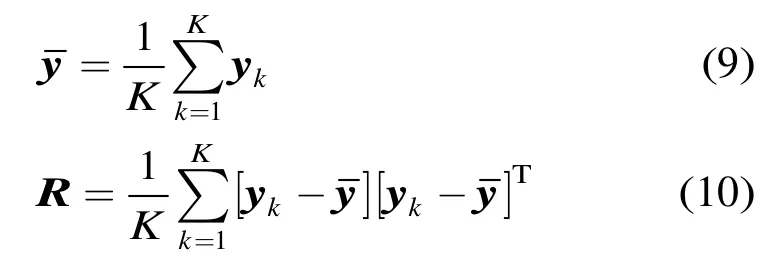
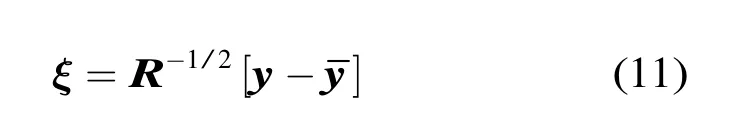
为简单起见，称ξ为待分类样本，对应特征平面上的一个点。纯海杂波特征序列yk,k=1,2,…,K通过式(11)归一化处理后，称为训练样本ξk,k=1,2,…,K，对应特征平面上的K个点。

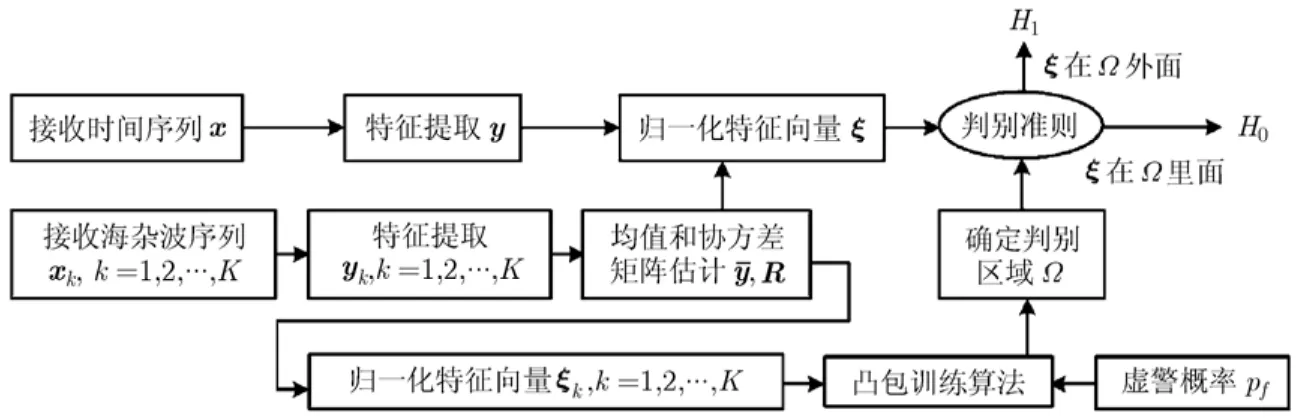
图2 本文算法原理框图

3.2 确定判别区域Ω

基于奈曼-皮尔逊准则[10]，最佳的判别区域Ω由下式确定

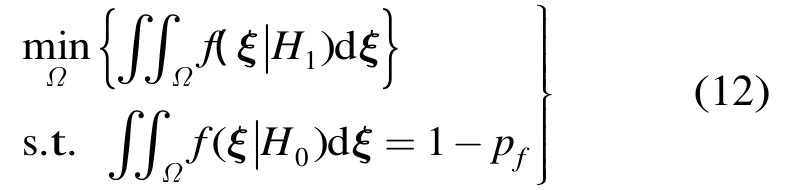
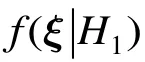
其中#{A}表示集合A中元素的个数。确定判别区域Ω可以描述为：给定pf，得到由K(1 -pf)个训练样本组成的凸集。

针对式(13)的优化问题，采用文献[9]的凸包训练算法获得判别区域Ω：确定训练样本集合的聚类中心，从训练样本集合Θ={ξk,k= 1 ,2,…,K}中删去离聚类中心的马氏距离[9]最远的Kpf个样本，剩下的K(1 -pf)个训练样本构成新的集合Θ1= {ξk,k= 1 ,2,… ,K(1 -pf)}，利用集合Θ1中的样本组成的凸包作为判别区域Ω。

凸包[9]是指包含集合Θ1中所有元素的最小凸集，由一个凸多边形组成，设vi,i= 1,…,I是凸包的I个顶点，它们是顺时针排列的，vi∈Θ1，且vI+1=vI。凸包定义为[9]

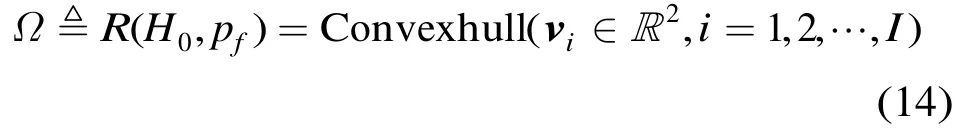
式(14)所得到的凸包并不一定是式(12)中Ω的最优解，在计算代价允许的前提下，读者可以考虑使用其它的凸包训练算法。

3.3 判别准则

确定判别准则就是要确定ξ与Ω的位置关系。如果ξ在Ω里面，当且仅当式(15)成立[9]

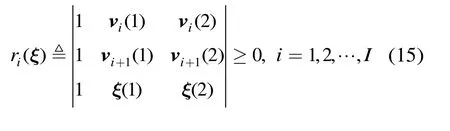
从式(15)可以看出，只要ξ为凸包内的点，对于所有的i，都有ri(ξ) ≥ 0 。如果ξ为凸包Ω外的点，对于某些i,ri(ξ) ≥ 0 ，对于另一些i,ri(ξ) ＜ 0 。故只要存在一个i，使得ri(ξ) ＜ 0 ，我们就可以判定ξ在Ω外。基于上述分析，定义判别函数为

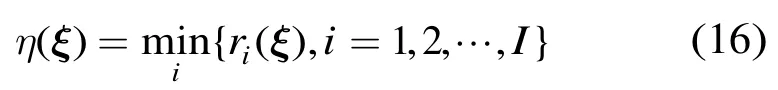
则式(4)的分类问题使用如下的判别准则：如果η(ξ)≥ 0 ，将x(n)判为ω，说明x(n)中不含目标；否则不判为ω，说明x(n)中包含目标。该判别准则正好与式(3)相对应。

根据式(14)确定的Ω，用式(16)的判别函数可确定目标是否存在。

3.4 计算复杂度分析和样本选择

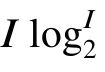
表1 3种算法的计算复杂度

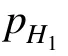
4 实验结果

本节使用IPIX雷达[12]采集的4组实测数据来评价本文算法的检测性能，并与文献[7]中两种算法的性能进行了比较。实测数据分别为 19980223-172410(目标所在单元为32th，影响单元为19th-32th，雷达在方位上扫描 4.5o，距离分辨率R=3m)，19980223-173950(目标所在单元为27th，影响单元为24th-30th，雷达为驻留模式，R=9m), 19980223-170435(目标所在单元为25th，影响单元为23th-27th，雷达在方位上扫描 4.5o,R=15m, 19980223-164055(目标所在单元为31th，影响单元为30th-31th，雷达为驻留模式，R=30m)。这4组数据包括60000组脉冲和34个距离单元，数据的其它参数详见文献[12]。我们对脉冲数据采取长度为10的滑窗处理以保证较小的pf。将目标所在单元的数据作为待分类样本，将纯海杂波数据作为训练样本。目标是直径为1 m的塑料球，表面包裹着金属丝，用固定在海底的锚牵引着，塑料球随着海浪的运动而上下起伏。

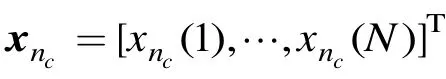
从图3中可以看出，当分辨率为3 m, 9 m和15 m时，目标所在单元的回波的平均功率在大多数时刻小于纯杂波单元和影响单元的回波的平均功率，目标的存在不但没有使回波功率增强反而使回波功率减弱了，这表明，高分辨海杂波背景下的漂浮目标回波不能用加性模型建模，必须用非加性模型建模，结合图1(b)，我们验证了式(1)给出的非加性模型的合理性。当分辨率为30 m时，目标所在单元与纯杂波单元和影响单元的回波的平均功率三者是重叠在一起的，目标的存在没有使回波功率减弱，当然也没有使其增强，这是因为实测的小目标体积很小，来自目标的回波能量较弱，它对该单元的回波功率贡献很小，可以使用加性模型建模，这表明，当分辨率较低时，用加性模型建模是合理的。

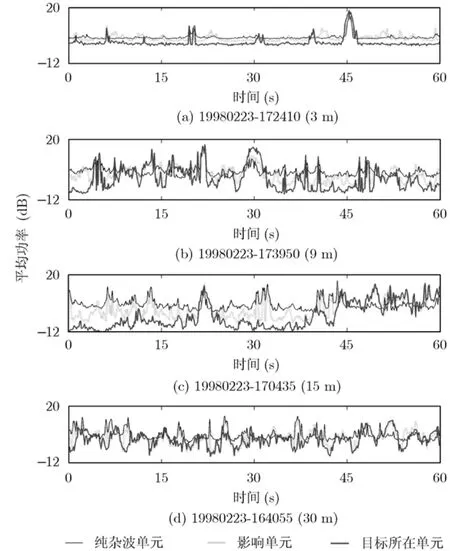
图3 4组数据的平均功率

图4为训练样本和待分类样本在2维特征平面的显示图，其中，实验数据和参数为：19980223-172410, HH极化，N=64,K= 1 00,000。图4(b)为pf= 0 .001时，删去 100个训练样本后组成的凸包以及待分类样本在2维特征平面的显示图。从图4(c)中可以看出，利用凸包可以将大量待分类样本与训练样本分开。将训练样本和待分类样本向横轴或者纵轴投影时，二者都是无法分开的。由于训练样本和待分类样本分别是海杂波特征向量和接收回波特征向量的仿射变换，根据仿射不变性，则单个特征是不可分的，进一步验证了单个特征检测算法的缺陷。

表2 给出了虚警概率pf= 0 .001,N=64,K=100,000时，利用4组数据计算的检测结果。可以看出，首先，本文算法在3 m, 9 m, 15 m的数据不同极化方式(HH, HV, VH, VV)下的检测性能都明显优于Rayleigh和Entropy算法的性能，这是因为文中考虑了两个特征的联合特性，Rayleigh和Entropy算法只考虑了单个特征，根据图4的分析结果，利用单个特征无法分开目标与杂波，利用两个特征可以分开目标与杂波；其次，本文算法的性能随着距离分辨率的提高而变好，这与高分辨海杂波下的非加性模型紧密相关，当分辨率较低时，例如 30 m,As+Ainfective＜A,α接近 1,cs(n)可以忽略，接收回波为加性模型，目标所在单元仍然有大量未受影响的海杂波，使得来自该单元的回波的散射特性与纯海杂波的散射特性之间的差异很小，难以利用特征来区分，故其性能不好。而当分辨率较高时，例如3 m，式(1)中的cs(n)不能忽略，α≪1，接收回波为非加性模型，漂浮的小目标几乎影响了整个雷达分辨单元的微细结构，来自该单元的回波的散射特性不同于纯海杂波的散射特性，故其检测性能变好；最后，无论雷达工作在驻留模式还是扫描模式，本文算法均能获得好的检测性能，不受雷达工作模式的限制。

读者可能会注意到，我们没有比较本文算法与基于非线性预测方法[4]以及基于分形方法[5,6]之间的性能差异，这是因为基于非线性预测方法和基于分形方法要求时间序列的观测时间很长，在本文的实验条件下，无法进行这两类算法的实验，而且从文献[4-6]实验结果可以看出，本文算法的性能更好。

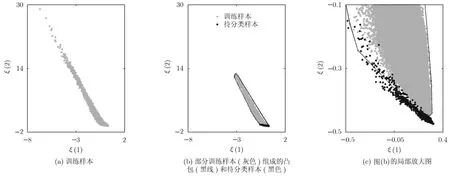
图4 不含目标的训练样本和含有目标的待分类样本在2维特征平面的显示图

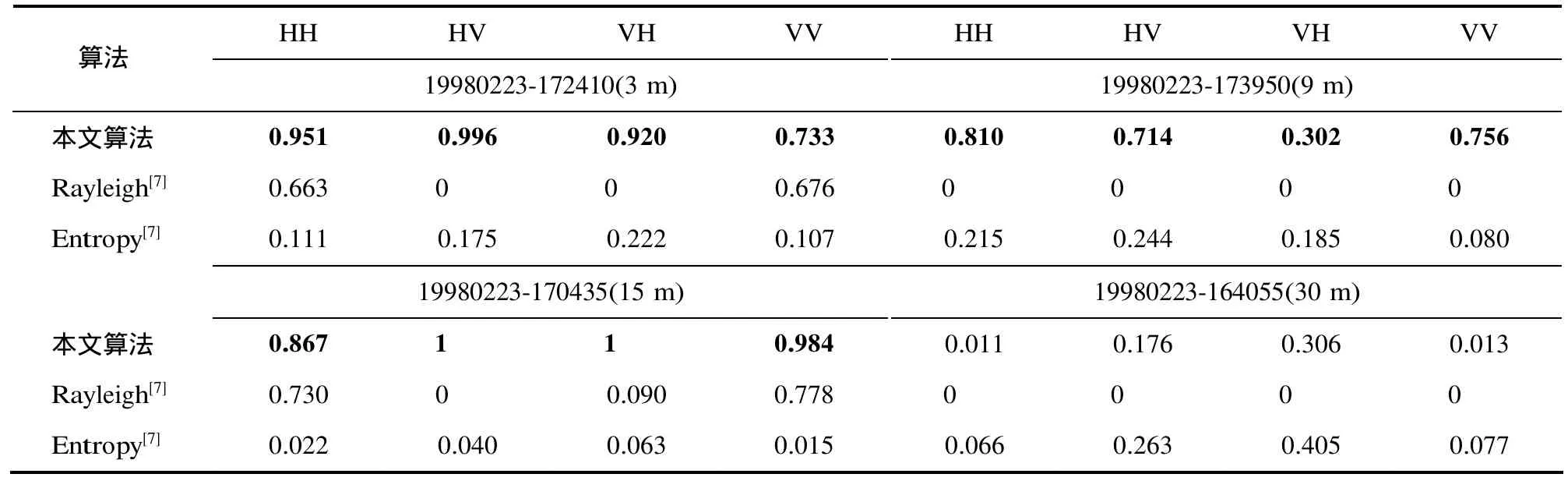
表2 不同分辨率数据的4种极化下的检测概率Pd，其中pf=0.001, N=64

图5为本文算法，Rayleigh和Entropy算法的ROC性能比较曲线，所用的数据和参数为19980223-173950, HH极化，N=64,K= 1 00,000。从图5中可以看出，本文算法的检测性能明显优于Rayleigh 和Entropy算法。由于实测数据样本有限，使用蒙特卡罗算法确定判别区域时，我们所能得到的最小虚警概率为0.001。

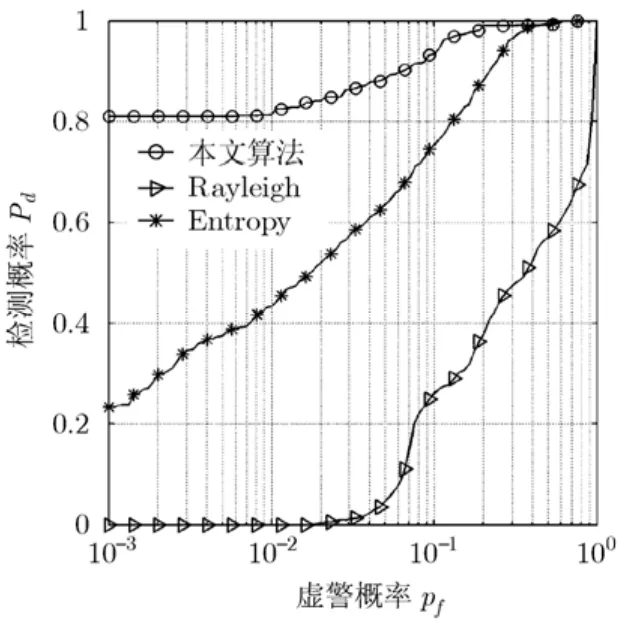
图5 本文算法，Rayleigh算法和Entropy算法的ROC性能曲线

表 3 给出了pf=0.001,N= 1 28,K=100,000时，4组数据的实验结果。本文算法仍然优于Rayleigh和Entropy算法。同时，对比表2的结果可知，本文算法的检测性能随向量维数N的增加而变好。这是由于两个特征都与多普勒域的频率分辨率有关，N越大，频率分辨率越好，多普勒谱熵就越接近其真实值，故本文算法在N= 1 28时的检测性能优于N=64时的检测性能。当然，N的增加既带来了计算量的增加，又需顾虑到海杂波的平稳时间长度。当雷达工作在扫描模式时，还需考虑波束驻留时间、脉冲重复时间等因素。在实际应用中，若雷达工作在扫描模式，一般取N=64，若雷达工作在驻留模式，可取N= 1 28。

5 总结

检测漂浮小目标存在着一些难题，诸如回波模型的改变、参数估计困难等，已有的单个特征检测算法不能获得理想的检测性能。本文首先分析出漂浮目标回波在高距离分辨海杂波中满足非加性模型，给出了该模型的解析式，然后为了避开该模型下对α的估计和对cs(n)的建模，将检测问题转化为分类问题，提出了特征联合检测算法。实测IPIX雷达数据实验结果表明，本文算法在高分辨海杂波下的检测性能优于Rayleigh和Entropy算法，不受雷达工作模式的限制，为监视雷达检测漂浮小目标和分布式目标提供了一种新的检测方案。

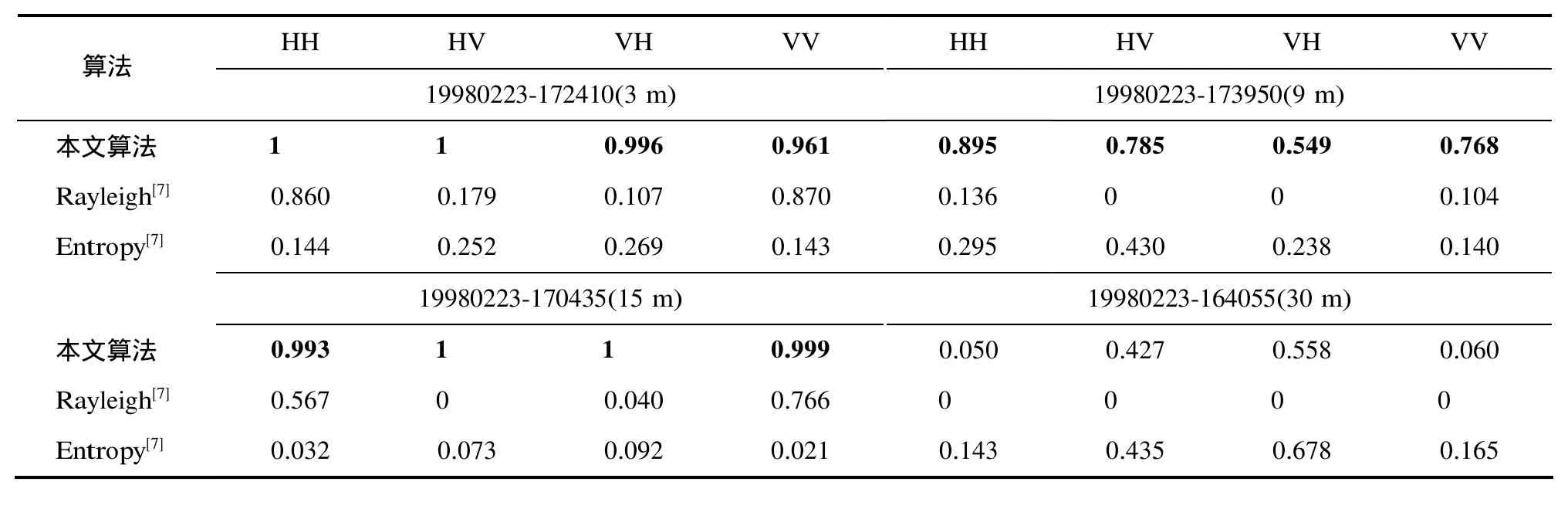
表3不同分辨率数据的4种极化下的检测概率Pd，其中pf=0.001, N=128

[1]Ward K D, Tough R J A, and Watts S. Sea clutter: scattering,the K distribution and radar performance. Published by the Institution of Engineering and Technique, London, United Kingdom, 2006.

[2]Shi Y L and Shui P L. Target detection in high-resolution sea clutter via block-adaptive clutter suppression.IET Radar,Sonar and Navigation, 2011, 5(1): 48-57.

[3]Maio A D, Farina A, and Foglia G. Knowledge-aided Bayesian radar detectors & their application to live data.IEEE Transactions on Aerospace and Electronic Systems,2010, 46(1): 170-183.

[4]Leung H, Daubash N, and Xie N. Detection of small objects in clutter using a GA-RBF neural network.IEEE Transactions on Aerospace and Electronic Systems, 2002,38(1): 98-118.

[5]Hu J, Tung W W, and Gao J B. Detection of low observable targets within sea clutter by structure function based multifractal analysis.IEEE Transactions on Antennas Propagation, 2006, 54(1): 136-143.

[6]Xu X K. Low observable targets detection by joint fractal properties of sea clutter: an experimental study of IPIX OHGR datasets.IEEE Transactions on Antennas Propagation, 2010, 58(4): 1425-1429.

[7]Wang X, Liu J, and Liu H W. Small target detection in sea clutter based on Doppler spectrum features. Proceedings of 2006 CIE International Conference Radar, Shanghai, China,2006: 1289-1292.

[8]关键, 刘宁波, 张建, 等. 海杂波的多重分形关联特性与微弱目标检测. 电子与信息学报, 2010, 32(1): 54-61.

Guan Jian, Liu Ning-bo, Zhang Jian,et al.. Multifractal correlation characteristic of real sea clutter and low-observable targets detection.Journal of Electronics&Information Technology, 2010, 32(1): 54-61.

[9]Shui P L, Liu H W, and Bao Z. Range-spread target detection based on cross time-frequency distribution features of two adjacent received signals.IEEE Transactions on Signal Processing, 2009, 57(10): 3733-3745.

[10]Van Trees H L. Detection, Estimation, and Modulation Theory. Part I. New York: John wiley & sons, INC., 2003: 33.

[11]Haselgrove C B. A method for numerical integration.Mathematics of Computation, 1961, 15(76): 323-337.

[12]Haykin S. The McMaster IPIX radar sea clutter database in 1998. [Online]http://soma.mcmaster.ca/ipix. php.