基于混沌压缩感知的稀疏时变信号在线估计
陈胜垚 席 峰 刘 中
(南京理工大学电子工程系 南京 210094)
1 引言
压缩感知(CS)理论是由Donoho[1]和Candes等人[2]从信号稀疏分解和逼近理论发展而来的一种新的信号低速率获取理论,其核心思想是对信号同时进行压缩处理和采样。当信号是稀疏信号时,信号压缩测量通过随机线性投影,将高维信号映射到低维信号;当随机线性投影满足约束等距性(RIP)条件[3]时,该稀疏信号可以精确重构。
在初期的CS理论研究中,假定稀疏信号是固定时间长度的;然而在很多实际应用中,稀疏信号通常是时变的,因此稀疏时变信号的CS理论研究受到了人们的关注。稀疏时变信号是指信号展开系数时变的稀疏信号[4],系数时变有稀疏位置和幅度两种时变的可能。对稀疏位置已知而仅幅度时变时的信号,稀疏时变信号退化为一般时变信号,可采用最小均方(LMS)算法或递归最小二乘(RLS)算法估计时变的幅度,因此稀疏时变信号的CS主要针对稀疏位置时变信号的研究。在过去的几年里,针对稀疏时变的CS,人们提出了块处理和序处理两类算法[4-7]。块处理算法假设在一段时间内信号的稀疏结构和稀疏系数的幅度保持不变,而在不同的时间段信号的稀疏结构和稀疏系数的幅度发生变化,因此,可通过对稀疏信号分块处理的方式实现“块时变信号”的CS[4]。序处理算法主要研究的是稀疏系数快变的信号,即每个新的测量时刻稀疏信号的稀疏结构和稀疏系数的幅度都可能发生改变的信号。人们基于不同应用背景和目标函数提出了不同的CS方法,详见文献[5-7]。
上述稀疏时变信号在线估计方法均建立在线性测量的基础上,本文将研究基于混沌非线性测量的稀疏时变信号在线估计问题。混沌压缩感知(Chaotic Compressed Sensing, ChaCS)是文献[8]首次提出的一种基于混沌系统的非线性压缩感知理论。其基本思想是将稀疏信号激励混沌系统,根据混沌信号的类随机行为,产生具有随机性的输出,混沌系统输出的降采样即为压缩测量。ChaCS测量系统与基于随机滤波的线性测量系统[9]类似,其中混沌系统起到了随机滤波的作用;与随机滤波线性测量系统相比,ChaCS测量系统不仅实现结构简单,同时混沌系统对稀疏信号的混沌化过程增加了压缩测量数据的保密性。在信号重构方面,ChaCS根据混沌系统脉冲同步理论实现信号重构。构造一个激励信号是可编程信号源的响应混沌系统,其中可编程信号源由控制算法决定,当响应混沌系统同驱动混沌系统同步时,可编程信号源的输出即为重构的稀疏信号。在信号异地重构时,如第2节所述,不需要从测量系统传输大量测量系统数据至ChaCS重构系统。
本文将ChaCS理论扩展到稀疏时变信号情况下,根据现有的ChaCS重构系统,以离散时间稀疏时变信号为例,建立基于RLS准则的稀疏约束目标函数,通过求解不同时刻的稀疏约束目标函数,实现对稀疏时变信号的在线估计。为了验证本文方法的正确性,本文以Henon系统为例仿真分析频域稀疏时变信号的估计性能,仿真结果表明了该方法的有效性。
2 混沌压缩感知
在图1(a)所示的ChaCS测量系统中,假设驱动混沌系统是一个P维离散混沌系统:

其中x∈RP,F(xn,t) ∈RP分别是系统式(1)的状态向量及非线性矢量函数。在实现稀疏信号测量时,将稀疏信号sn激励系统式(1)。不失一般性,假定sn加载在第1个状态变量上,则P维离散自治混沌系统变为P维离散非自治混沌系统。
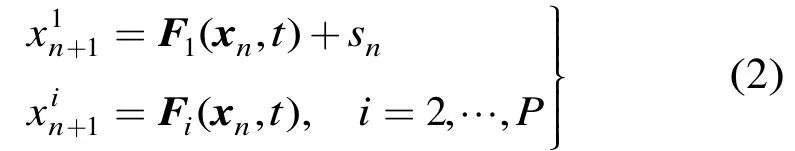
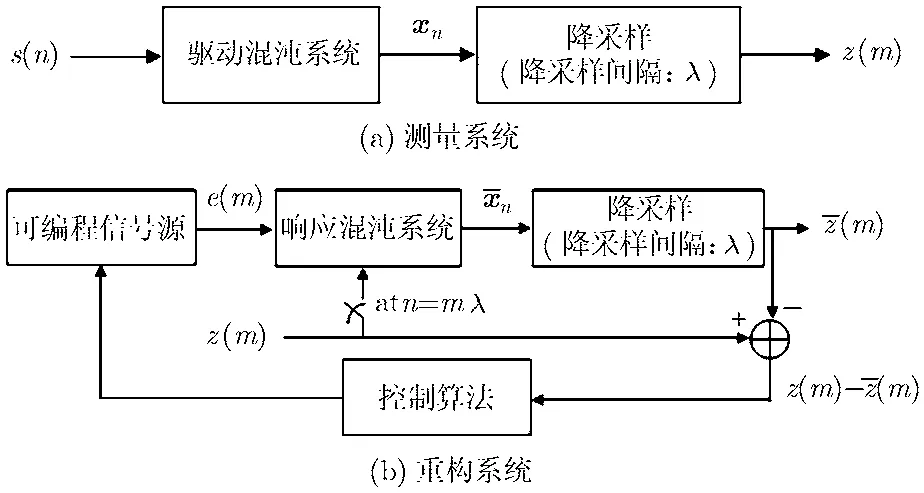
图1 混沌压缩感知实现结构
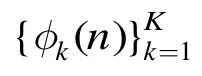
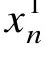

其中l为采样间隔。我们将降采样序列zm称为信号sn的压缩测量,而l称为降采样率。当sn为长度为N的有限长度信号时,降采样序列的长度为M=N/l。
为了重构稀疏信号sn,我们可构造如图1(b)所示的同步系统,其中响应混沌系统的系统结构与系统式(2)一致。
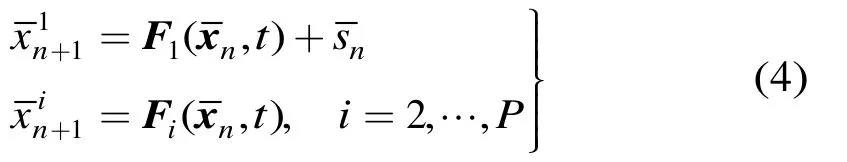
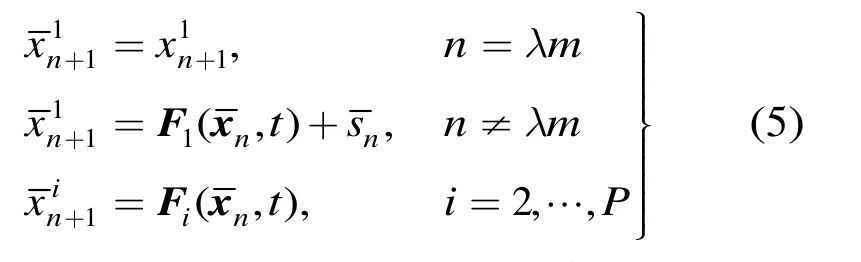
与式(3)类似,我们以l为采样间隔对进行降采样可得到降采样序列为

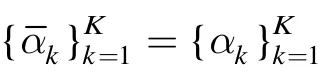
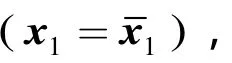
控制算法的设计是 ChaCS重构系统的核心问题之一。由系统式(5)可知,可表示为如下形式:
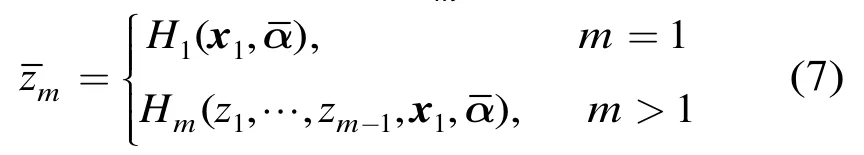
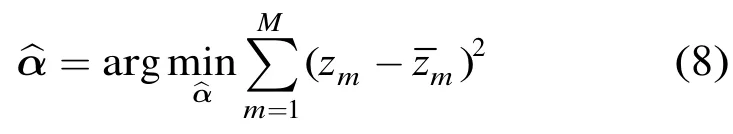
当稀疏信号sn,可采用稀疏正则化NLS的代价函数提高估计性能。
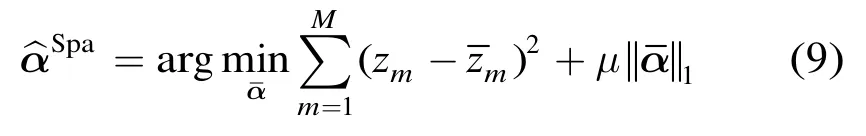
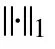
3 基于混沌压缩感知的稀疏时变信号在线估计
3.1 在线估计原理
在实际应用中很多信号是时变的,而式(9)中的正则化的NLS准则仅适用于估计固定激励信号的系数,当激励信号的系数时变时,式(9)不能实时估计时变系数a。同文献[6,7]思想一致,我们可以构造l1范数正则下的稀疏信号的非线性递归最小二乘(NRLS)估计为
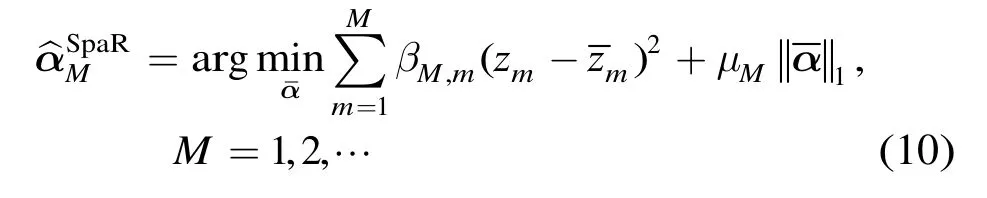
其中mM> 0 表示正则化参数,bM,m表示遗忘因子,式(10)被称为稀疏NRLS(Sparse NRLS, SpaNRLS)估计。通过选择不同的遗忘因子,NRLS对NLS准则下的代价函数进行了不同的加窗处理,从而能够实时估计时变系数。
遗忘因子选择通常有无穷长矩形窗、无穷长指数衰减窗和有限长矩形窗3种形式[7]。对无穷长矩形窗,每个观测数据具有相同的加权系数,这时式(10)的计算退化到文献[8]中采用的估计方法。对无穷长指数衰减窗,随着观测数据的增加,式(10)的计算复杂度增加,实现起来困难。有限长矩形窗可保持式(10)的计算复杂度,实现相对简单。为此,本文主要研究基于有限长矩形窗加权的稀疏时变信号的在线估计。
3.2 重构算法
在有限长矩形窗加权情况下,式(10)转化为
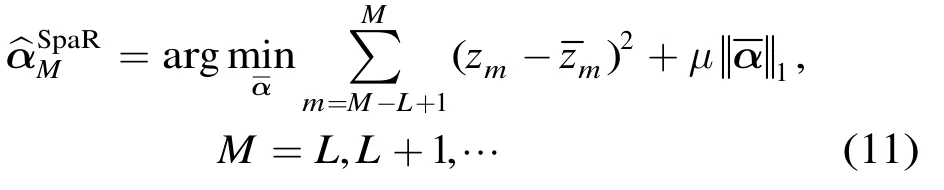
其中L是有限长矩形窗长度。在式(10)和式(11)中,观测函数是的非线性函数,M+1时刻的目标函数不能由M时刻的目标函数递归表示,目前还没有有效的算法能够递归求解,每一时刻的目标函数要独立求解。但是,我们可以用“热启动”思想[11]来求解,即以为初始搜索点,该方法可以提高算法的收敛速度。压缩测量每向前滑动一个采样脉冲会得到一个新的目标函数,以M=L时刻式(11)的解为初始解,迭代求解不同时刻的稀疏系数估计。
本文借鉴文献[12]中迭代加权最小二乘算法利用加权l2范数逼近l1范数的思想,提出一种迭代加权非线性最小二乘算法(Iterative Reweight Nonlinear Least-Squares, IRNLS),从而使式(11)中的l1正则NLS问题转化为一系列NLS问题。
在给定的观测时刻M, IRNLS算法的具体流程
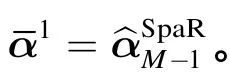
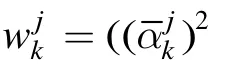
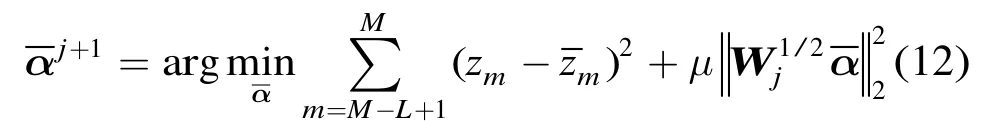
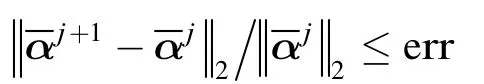
有限长矩形窗长度L的选择会影响式(11)的求解性能,当L较小时,求解目标函数更容易到达局部最优解,而选择较大的L则会导致式(11)的计算复杂度增加,因此在实际应用时我们倾向于在能够估计出系数的前提下尽可能选择较小的L。另外,有限长矩形窗可以每次向前滑动多个观测点,当矩形窗每次向前滑动d个观测点时(1<d≤L),式(11)转化为如下形式:
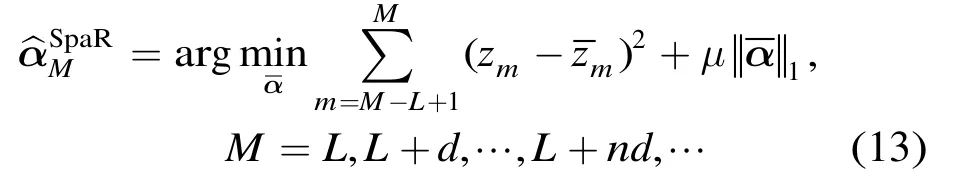
如果稀疏信号的系数慢时变,可以选择较大的d以减少式(13)中问题求解的次数,从而降低计算量。
4 仿真分析
本文以激励信号是频域稀疏时变信号的 Henon系统为例仿真研究 SpaNRLS算法估计稀疏时变信号的性能。下面对有限长矩形窗时 SpaNRLS算法性能进行仿真分析。外加激励Henon混沌系统如下所述:
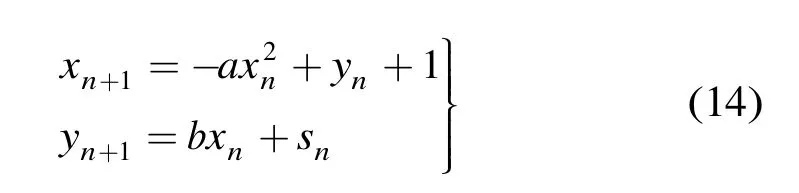
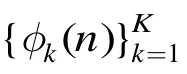
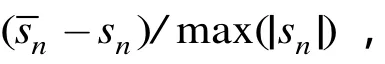
实验2研究不同的时间窗滑动距离d对SpaNRLS算法估计时变系数性能的影响。试验中有限长矩形窗长度为L=64,每次向前滑动的距离分别取d= 1 ,4,8,16个观测点。时变系数的相对估计误差如图3所示,选择不同的d, SpaNRLS算法均可以正确地估计出时变系数。当d较小时,SpaNRLS算法可以更快速地跟踪时变系数的变化,但此时求解式(13)的次数也相应增加,从而需要更大的计算量。而当d较大时,SpaNRLS算法跟踪时变系数的速度变慢,不过此时求解式(13)的次数减小了,使得计算量也相应减少。通过d的适当选择可折中考虑实现计算量和跟踪时变系数的性能。
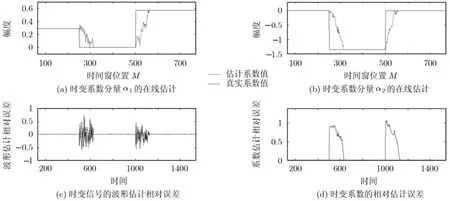
图2 频域稀疏时变信号的估计性能
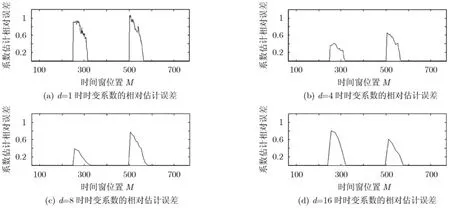
图3 不同时间窗滑动距离时稀疏时变系数的估计性能
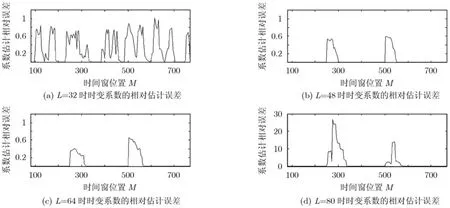
图4 不同矩形窗长度时稀疏时变系数的估计性能
实验3研究不同的矩形窗长度L对SpaNRLS算法估计时变系数性能的影响。试验中选取d=4,窗长分别为L= 3 2,48,64,80。时变系数估计的相对误差如图4所示,为了便于比较,不同窗长情况下均选择M=80为式(13)的初始求解时刻。由图可知,当时间窗长度L较小时(L=32), SpaNRLS算法不能正确估计出时变系数,因为L较小时式(12)可能存在更多的局部最优解,从而更容易产生错误的系数估计。当L较大时,正确估计出时变系数所需的时间增加了,这是因为时间窗跨越系数跳变时刻所持续的时间增加了。同时由于L的增加导致式(13)中NLS问题的维数增加,目标函数对参数变化更加敏感,在时间窗跨越系数跳变时刻所持续的时间内相对估计误差也相应增大,但最终能够正确估计出时变系数。因此适当选取较小的窗长L可以提高跟踪时变系数的速度,同时较小的L还可以减小式(13)中NLS问题的维数,从而降低问题求解的计算复杂度。
5 结论
ChaCS是一种基于混沌系统的非线性压缩感知方式,本文将这种压缩感知推广到稀疏时变信号情形。针对ChaCS结构,本文构造了基于RLS准则的SpaNRLS估计算法,使得ChaCS能够在线估计稀疏时变信号。SpaNRLS算法首先形成一个 RLS准则下的稀疏约束目标函数,然后利用IRNLS算法求解该目标函数,通过选择适当的遗忘因子,求解该目标函数可以正确估计出稀疏时变信号的系数。离散时间信号仿真实验表明本文思想和方法是正确的和可行的。本文阐述的稀疏时变信号的ChaCS思想不仅适用于离散时间信号也适用于连续信号。
[1]Donoho D. Compressed sensing [J].IEEE Transactions on Information Theory, 2006, 52(4): 1289-1306.
[2]Candes E, Romberg J, and Tao T. Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information [J].IEEETransactionson Information Theory, 2006, 52(2): 489-509.
[3]Candes E and Tao T. Decoding by linear programming [J].IEEE Transactions on Information Theory, 2005, 51(12):4203-4215.
[4]Vaswani N. Kalman filtered compressed sensing [C]. IEEE International Conference on Image Processing (ICIP), San Diego, 2008: 893-896.
[5]Chen Y, Gu Y, and Hero, III A O. Sparse LMS for system identification[C]. IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Taipei,2009: 3125-3128.
[6]Babadi B, Kalouptsidis N, and Tarokh V. SPARLS: the sparse RLS algorithm [J].IEEE Transactions on Signal Processing, 2010, 58(8): 4013-4025.
[7]Angelosante D, Bazerque J A, and Giannakis G B. Online adaptive estimation of sparse signals: where RLS meets thel1-norm [J].IEEE Transactions on Signal Processing, 2010,58(7): 3436-3447.
[8]Liu Z, Chen S Y, and Xi F. A compressed sensing framework of frequency-sparse signals through chaotic systems [J]. http://arxiv.org/abs/1112.3212.2011.12.
[9]Tropp J A, Wakin M, and Duarte M,et al.. Random filters for compressive sampling and reconstruction[C].International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Toulouse, 2006: 872-875.
[10]Yang T and Chua L O. Impulsive stabilization for control and synchronization of chaotic systems: theory and application to secure communication [J].IEEE Transactions on Circuits and System-I:Fundamental Theory andApplications, 1997, 44(10): 976-988.
[11]Figueiredo M, Nowak R, and Wright S. Gradient projection for sparse reconstruction: application to compressed sensing and other inverse problems [J].IEEE Journal of Selected Topics in Signal Processing, 2007, 1(4): 586-598.
[12]Daubechies I, DeVore R, Fornasier M,et al.. Iteratively reweighted least squares minimization for sparse recovery [J].Communications on Pure and Applied Mathematics, 2010,63(1): 1-38.
[13]Morini B and Porcelli M. TRESNEI, a Matlab trust-region solver for systems of nonlinear equalities and inequalities [J].Computational Optimization and Applications, DOI:10.1007/s10589-010-9327-5, 2010.

