基于遥感图像压缩的最佳小波分解层数研究
李卓凡
(韩山师范学院,潮州521041)
1 引言
随着航天科学技术的高速发展,遥感器的分辨率不断提高,遥感图像的数据量必然不断增加,这给有限的传输信道带宽带来沉重的传输压力。如何对遥感图像数据进行高保真、高压缩地传输,成为了当今一个重要的课题。
遥感图像的空间冗余较小,容量大,细节丰富。小波变换具有优异的时频局域性、多分辨性,以及良好的去相关能力,因此采用了基于小波变换的图像压缩技术。在基于小波变换的图像压缩算法中,嵌入式零树小波编码(EZW)是一种高效且简单的小波图像编码方法。在EZW算法的基础上,Said和Pearlman提出了分层树集合分裂算法(SPIHT)。它继承了小波系数的零树结构,针对消除树间冗余进行了改进,是一种更为高效的小波图像编码算法。在基于小波的图像压缩SPIHT算法的研究中,大多是针对于算法本身的改进研究,但忽略了小波分解层数对压缩效果的影响。小波分解的层数并不是越多越好,要根据图像的特征,及所选取的小波基来确定。
2 小波基的选取
小波变换,实质上是将图像信号投影到由小波基函数构成的函数空间中,得到小波分解系数,从理论上讲,由小波分解系数通过小波逆变换可准确重构信号。但实际上,并不是所有的小波基都适合图像分解,小波基必须依据以下的条件来选取:①正交性;②对称性及线性相位;③正则性;④消失矩阶数;⑤紧支撑性。
通常,在选择小波基时,首先考虑其对称性和正交性,一般会放弃一部分正交性而选择具有线性相位的双正交小波基,以减少感官误差;然后考虑其正则性和消失矩。正则性相同的情况下,消失矩阶数越高越好,在消失矩相同的情况下正则性阶数越高越好;最后,考虑其紧支性[2]。在文献[1-2]中,对常用于小波图像压缩的几个小波基进行详细的分析和对比,从文献的实验结果得出D9/7和D5/3最适合作为遥感图像压缩的小波基。
D9/7小波具有良好的能量集中性,消失矩较大,适用于有损压缩,算法如下:
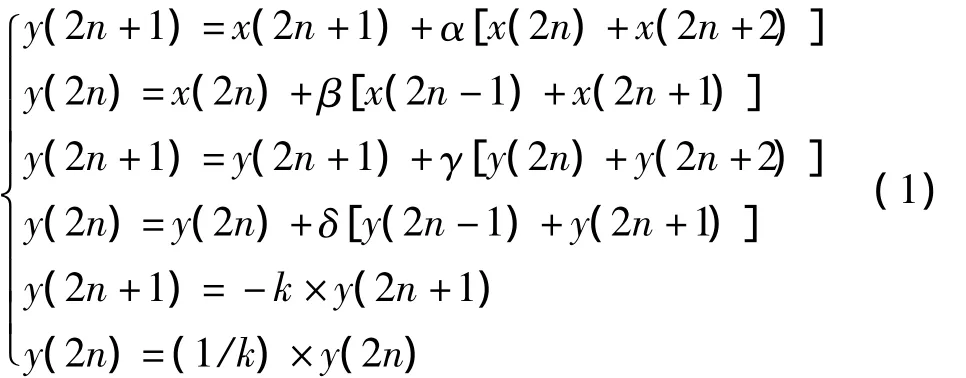
其中 α≈-1.586134342,β≈-0.05298011854,γ≈0.8829110762,δ≈0.4435068522,k≈1.149604398。
D5/3小波的支撑宽度小,紧支撑性好,适用于有损及无损压缩。其小波变换仅靠整数加法和移位完成,运算速度快,内存需求低。算法如下:
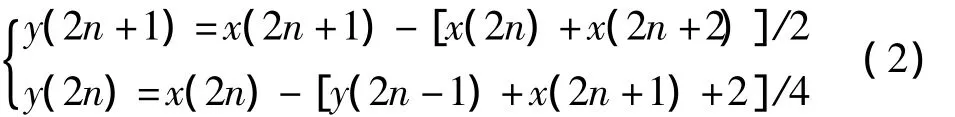
表1为这两个小波基各种参数的列表。本文采用D9/7小波及D5/3小波进行图像分解及重构。
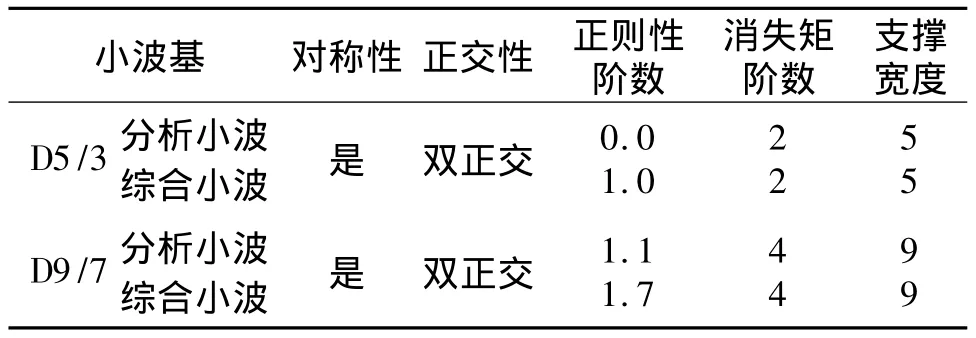
表1 D9/7、D5/3小波基性质参数
3 小波变换分解层数的选择
小波变换的级数越多,图像的频带就划分得越细,就越有利于图像的编码。但是由于上一级(较高层)频带分解的信号输出又作为下一级(较低层)频带分解的输入,级数增加意味着级联的滤波器越多,造成的信号移位也越大。另一方面,由于每次小波系数分解/重构都要进行边界延拓,级数越多引起的边界失真也越大。而且级数越多,硬件实现的复杂度和存储量都要增加。所以实际应用中,确定小波分解/重构的级数要兼顾不同方面的影响。
一幅图像经过小波变换以后,可分解为一个低频子带和水平、垂直、对角三个方向的高频子带,而低频子带又可以进一步地分解为四个子带。若分解层数为k,则总的子带数为3k+1。那么,图像分解成多少层才是合适的呢?这取决于三方面的因素:即图像的复杂程度;滤波器的长度;子图信息量。
理论上,若一副大小为M*N(假设M>N)的图像,滤波器长度为n,则小波分解的最大层数k必须满足关系式:

但是图像分解并不是越多层压缩效果越好,分解层数合理选择还关系到影响运算量和复杂度。从信息论的观点来看,熵的大小反映了信源的信息量,信源的熵值越大,压缩的可能性也越大。信号S的熵定义为:
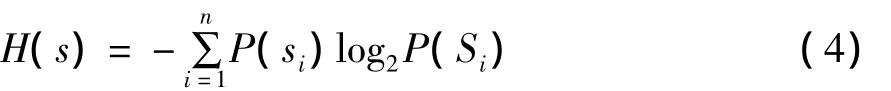
小波变换的一个重要目的就是减少熵,每一级离散小波变换将图像数据分成LL、LH、HL、HH四个子带。设第j层的低频子带为LLj,分解后的四个子带分别为:LLj+1、LHj+1、HLj+1、HHj+1,其熵值分别为:HLLj+1、HLHj+1、HHLj+1、HHHj+1,由于熵与编码所需的平均比特数直接对应,当一个子图分成四个子图,要求四个子图熵值的和应该变小,这样才能继续分解,实现数据的压缩。分解后四个子带编码所需的平均比特应小于分解前低频子带的平均比特数,即:

4 实验结果
为了更全面地分析不同分解层数对图像压缩的影响,本文选择了7种不同的图像大小为256×256像素的遥感图像进行实验:map1(城市建筑)、map2(城市建筑)、map3(水域和建筑)、map4(山峰和森林)、map5(水域和农田)、map6(水域和山)、map7(建筑和农田)。表2为7幅图像的熵:

表2 7幅不同图像的熵
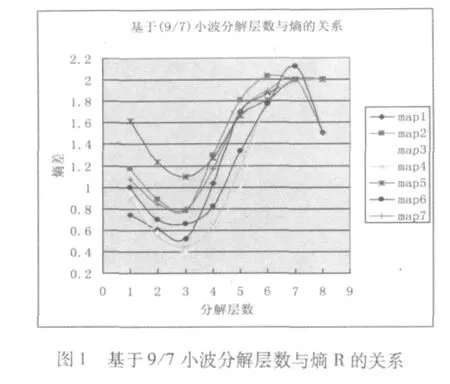
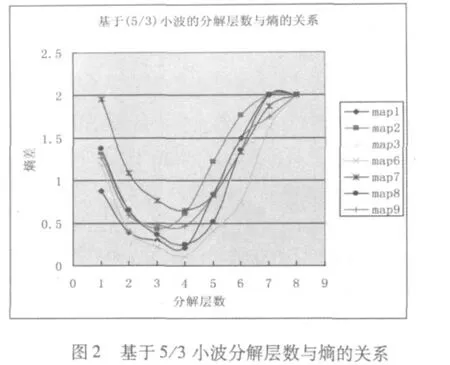
用D9/7、D5/3小波对各幅图像进行小波分解,然后根据式(2)计算各层分解图像的熵,最后根据(3)式计算每层分解后四个子带编码的熵值和分解前低频子带编码的熵值,并进行比较。计算出每次分解熵值的减小,并画出曲线,如图1、图2所示。图1为用D9/7小波分解得到的曲线图,图2为用D5/3小波分解得到的曲线图。图1中除了map6、map7外,从第5层开始,熵值减小趋于平缓,曲线变得平稳;图2则从第6层开始,熵值减小趋于平缓,曲线变得平稳。
接着,用D9/7和D5/3小波对7幅图像进行图像分解,用SPIHT算法对图像进行压缩、解压并重构,计算不同分解层数重构图像的峰值信噪比(PSNR),实验结果如图3、图4所示。从数据图表可以看出,用D9/7小波分解,随着分解层数的增加,重构图像的PSNR明显增大,但从第5层分解开始,重构图像的PSNR变化并不明显;用D5/3小波分解,同样各幅图像在前面几个层次分解重构后,PSNR增大,从第4层到第6层、第8层分解后重构的PSNR是趋于平稳的,只有在第7层时有点波动。
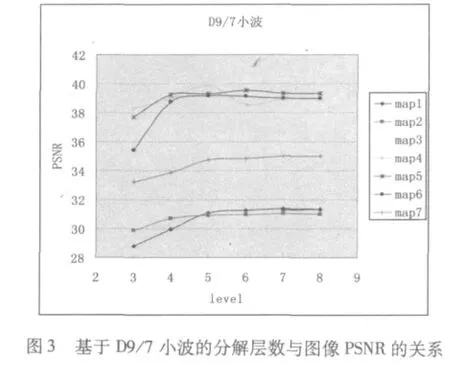
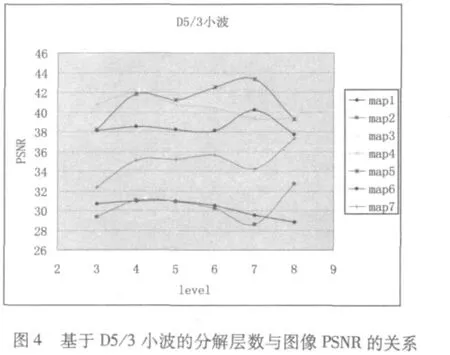
数据结果显示,对于遥感图像小波分解层数为5-6层为最佳分解层数,作更多的分解并不能明显改善图像效果。从图3、图4中可以看出,D9/7更适用于遥感图像的小波变换,其信噪比更优于D5/3。图5-图7为map6分别用两种小波作5层分解,用SPIHT算法压缩图像,解压重构后的图像效果。从视觉效果看,作5层小波分解重构后的图像与原图区别不大,而图6要比图7光滑,噪声较小。

5 结束语
不同类型的图像经过小波变换后,其系数的分布特性是不同的,于是从理论上分析了不同图像对小波基的选择条件,综合各方面的性能,选择综合性能最好的双正交小波基的D9/7和D5/3小波对遥感图像进行小波变换。并从信息熵的角度分析了熵对小波分解层数的影响,小波分解后只有图像的熵减小了,分解才有意义,才能达到压缩的效果。最后通过实验结果,得出了遥感图像压缩的小波分解层数为5-6层压缩效果最好。
[1] 柯丽,黄廉卿.适于遥感图像实时压缩的小波基的选择[J].光学技术,2005(1):77-83.
[2] 赫华颖,陆书宁.几种小波基在遥感图像压缩中的应用效果比较[J].国土资源遥感,2008(9):27-31.
[3] 李战明,迟洋.图像压缩中小波基的选择研究[J].机械与电子,2009(5):18-21.
[4] 孙延奎.小波分析及其应用[M].北京:机械工业出版社,2005.
[5] 成礼智,王红霞,罗永.小波理论与应用[M].北京:科学出版社,2004.
[6] Daubechies I.Orthonomal Bases of Compactly Supported Wavelets[J].Commu.In Pure and Application Math,1988,41:906-996.
[7] Villasensor J D,Belzer B,Liad J.Wavelet Filter Evaluation for Image Compression[J].IEEE Trans.Image Processing,1995,4(8):1053-1060.

