双参数指数分布无失效数据的可靠性分析

翟艳敏

0 引言

在可靠性试验中，特别是在高可靠性，小样本问题的定时截尾试验中，常会遇到“无失效数据”。自从文献[1]发表以来引起国内外的重视，并且取得一些研究成果。文献[2]提出了配曲线方法；文献[3]、[4]分别提出极小χ2法和等效失效数法；文献[5]提出修正似然函数法；文献[6]从生存分析中的CLASS-K方法及条件期望着手，提出改进的CLASS-K；文献[7]～[11]利用先验分布给出可靠性参数的Bayes估计或者多层Bayes估计；文献[12]、[13]利用样本空间的序关系得到可靠性参数的置信限。以往的研究文献大多讨论参数的点估计，而对置信限的研究极少。本文旨在对双参数指数分布场合下的无失效数据，在μ已知和μ未知的两种情形下，分别给出可靠性参数的置信限，并结合实例进行验证所得结论的有效性、可行性。

1 无失效数据模型与可靠性参数置信限

1.1 无失效数据模型

对某产品进行m次定时截尾试验，截尾时间为ti(i=1,2,…,m)(t1＜t2＜…＜tm)，相 应 的 样 品 数 为ni(i=1,2,…,m)，总的样品数结果所有样品无一失效，称(ti,ni)(i=1,2,…,m)为无失效数据。

1.2 可靠性参数的置信限

设某产品的寿命服从双参数指数分布，分布函数为

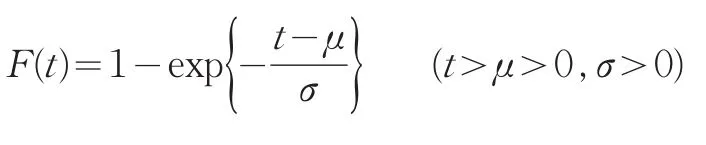
定理1设产品寿命服从双参数指数，T～Exp(t;μ,σ),其中μ已知，对产品进行m次定时截尾试验，结果无一失效，获得无失效数据 (ti,ni)(i=1,2,…,m)，，则σ的置信水平为1-α的置信下限为:

证明：寿命T～Exp(t;μ,σ),则一个产品在t时刻前失效的概率F(t)=P(T＜t)=若在第i次定时截尾试验中有 Xi个样品失效(Xi=1,2,…,ni,i=1,2,…,m)，则

由于产品的是失效率都很小，所以

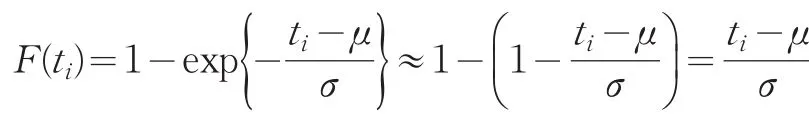
根据泊松定理有:

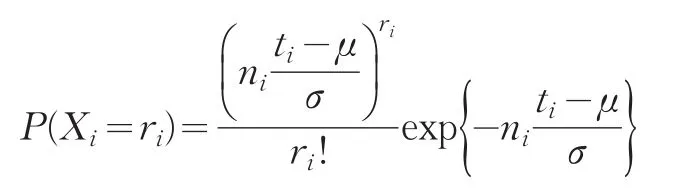
则事件{ }X1=r1,X2=r2,…,Xm=rm的联合概率为:

对于无失效数据情形，有:

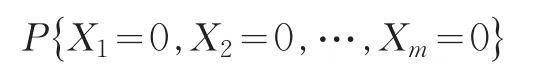
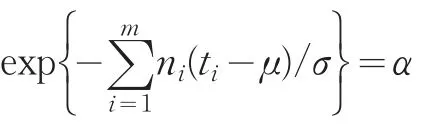
解得：

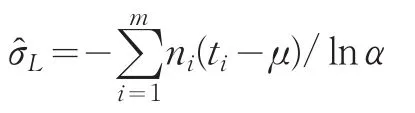
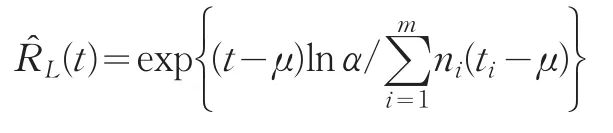
引理1设E是Z的所有可能值组成的集合，ϕ(u1,u2,…,u2n)是任何Borel函数，对任何z∈E，令：

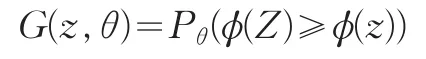
gL(Z)=inf{g (θ):G(Z,θ)＞ α}

则gL(Z)是g(θ)的置信水平为1-α的置信下限。

定理2设产品寿命服从双参数指数，T～Exp(t;μ,σ),其中μ未知，对n产品进行次定时截尾试验，结果无一失效，截尾时间为t1,t2,…,tn，则

σ的置信水平为1-α的置信下限为：

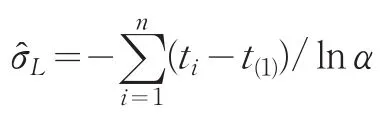
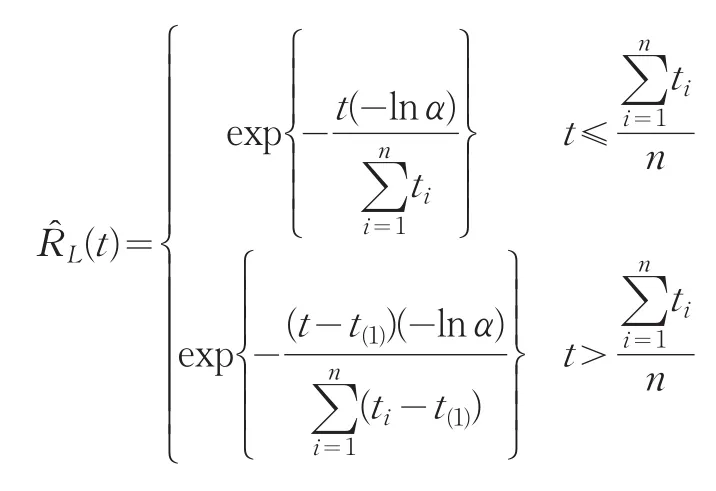
证明：对于无失效数据情形，由引理1有σ的置信水平为1-α的置信下限

其中：t(1)=min{ }t1,t2,…,tn

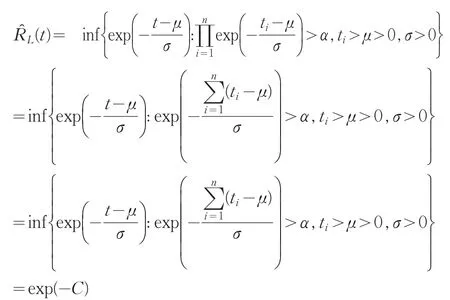
其中：

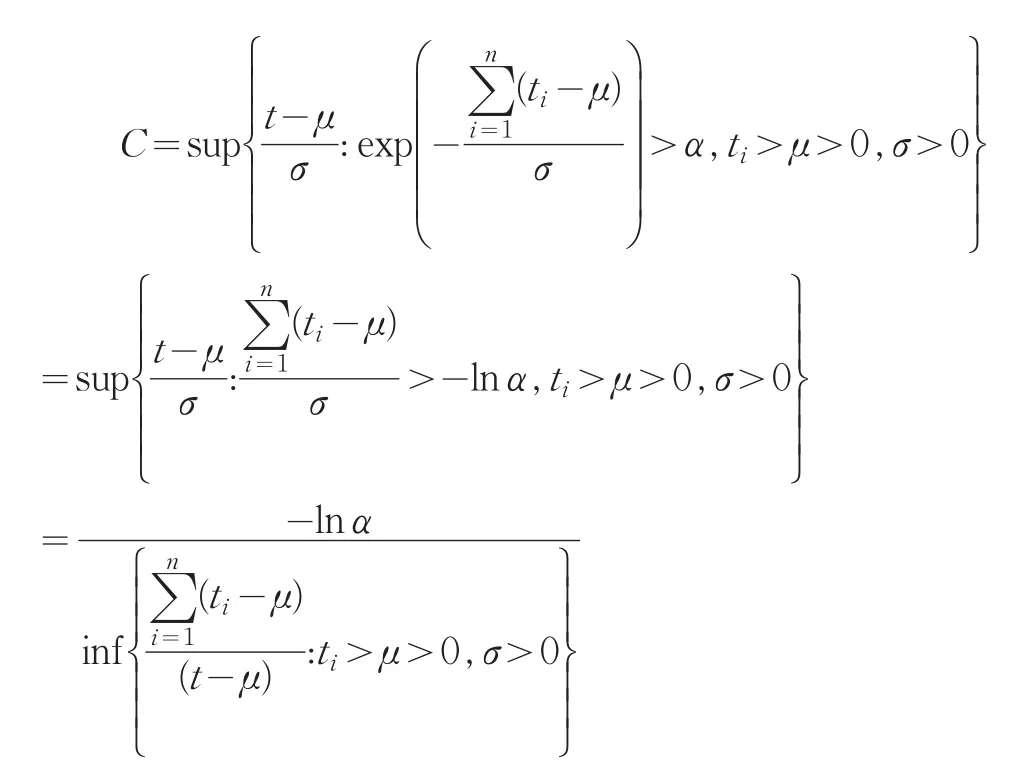
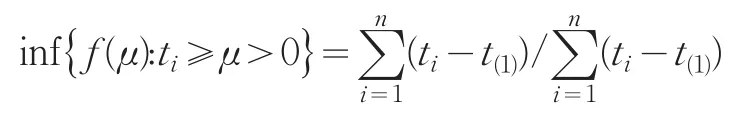
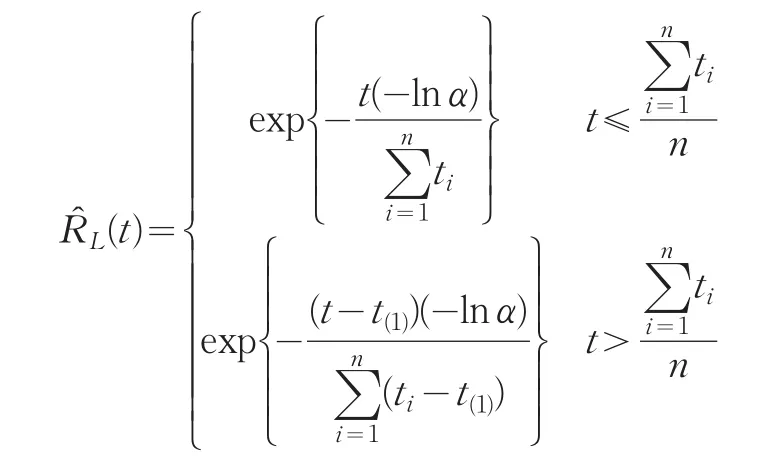
2 实例

上海萨澳液压传动有限公司生产的某型号发动机，其寿命服从双参数指数分布对该型号发动机做定时截尾试验，所得无失效数据如表1（单位时间：小时）。

表1 发动机的无失效数据

根据定理1，其中μ=100，计算结果如表2。

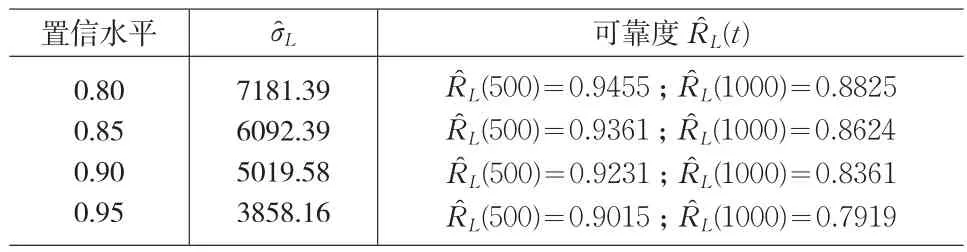
表2 μ已知时可靠性参数的置信限

根据定理2，计算结果如表3。

表3 μ未知时可靠性参数的置信限

从上述结果来看，利用定理1和定理2所得的结论，对于给定的不同的置信水平，可靠度的估计具有很好的稳健性，理论计算的结果与实际情况比较相符。

[1] Martz H F,Waller R A.A Bayes Zero-failure(BAZE)Reliability Dem⁃onstration Testing Procedure[J].Journal of Quality Technology,1979,11(3).

[2] 峁诗松，罗朝斌.无失效数据的可靠性分析[J].数理统计与应用概率，1989，4(4).

[3] 张忠占，杨振海.无失效数据的处理[J].数理统计与应用概率，1989.

[4] 张忠占，杨振海.等失效数在无失效数据分析中的应用[J].数理统计与应用概率，1991，6(3).

[5] 王玲玲，王炳兴.无失效数据的统计分析－修正似然函数方法[J].数理统计与应用概率,1996,11(1).

[6] 殷弘，杨瑛，丁邦俊等.关于无失效数据的分析[J].数理统计与应用概率，1996，11(3).

[7] 张继昌.无失效数据的Bayes分析[J].高校应用数学学报,1995,10(1).

[8] 韩明.无失效数据的多层Bayes可靠性分析[J].应用数学，1998，11(2).

[9] 韩明.失效概率的Bayes估计及应用[J].工程数学学报,2001,18(3).

[10] 翟艳敏.无失效数据的贝叶斯分析[J].统计与决策,2008,(11).

[11] 翟艳敏.威布尔分布的无失效数据分析[J].统计学评论,2009,5(1).

[12] Martz H F,Waller R A.Bayesian Reliability Analysis[M].New York:John Wiley and Sons,1982.

[13] Berger J O.Statistical Decision Theory and Bayesian Analysis[M].New York:Springer-Verlag,1985.