中考专题复习课的设计、生成与反思

☉江苏省海安县丁所初级中学 濮建平

中考复习是初中数学教学的重要环节，也是提高学生综合探究能力的重要一环，它没有固定的教材，也没有固定的模式，因此，教学的许多实际问题值得我们实践与思考.

课堂教学是一种有目标、求效率的活动，中考“专题复习课”更是如此.我们常常用效率和质量去评判和鉴赏一堂数学课，与此同时我们或许还要用“成本”的眼光去思考我们的学生学习，特别是初三最后的紧张复习阶段.这个成本是指学生上课达到的效果与所花的时间及投入的比.

近几年各地市的中考综合题中，基本图形改编的试题出现的概率较大，由于方法不当或思路不明，使解题难度加大.本人以2012年5月30日，笔者向同行展示的一节面向初三学生的中考专题复习课：“一个基本图形”改编的中考题为例，谈谈中考“专题复习课”的一些实践与思考，以期在初三最后的专题复习中取得较好的效果.

图1

一、教学设计简案

上课前动画演示基本图形（图1）.

1.考题引入，感受基本图形的变化

教师出示幻灯片.

例1（2011年永州市）探究问题：如图1，在正方形ABCD中，点E，F分别为DC，BC边上的点，且满足∠EAF=45°，连接EF，求证：DE+BF=EF（. 依次出示1—3小题）

（1）感悟解题方法，并完成下列填空：

如图2，将△ADE绕点A顺时针旋转90°得到△ABG，G

图2

此时AB与AD重合，由旋转可得：

AB=AD，BG=DE，∠1=∠2，∠ABG=∠D=90°，

所以∠ABG+∠ABF=90°+90°=180°.

因此，点G，B，F在同一条直线上.

因此∠EAF=45°，所以∠2+∠3=∠BAD-∠EAF=90°-45°=45°.

又∠1=∠2，所以∠1+∠3=45°.

即∠GAF=______.

又AG=AE，AF=AF，

所以△GAF≌______.

所以______=EF，故DE+BF=EF.

（2）方法迁移：

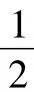
（3）问题拓展：

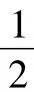
选题意图：这是一道经典的初中几何证明题，每年各个地方的中考试题均会出现以此图形为基础的变式考题，本课正是围绕本图形展开的.

2.尝试应用，巩固提高

教师出示幻灯片，学生练习.

例2（2008年大兴安岭市）已知在正方形ABCD中，∠MAN=45°，∠MAN绕点A顺时针旋转，它的两边分别交CB、DC（或它们的延长线）于点M、N.当∠MAN绕点A旋转到BM=DN时（如图5），易证BM+DN=MN.

图5

图6

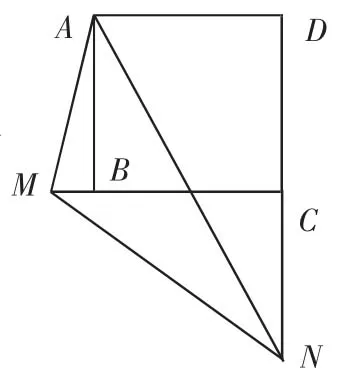
图7

（1）当∠MAN绕点A旋转到BM≠DN时（如图6），线段BM、DN和MN之间有怎样的数量关系？写出猜想，并加以证明.

（2）当∠MAN绕点A旋转到如图7的位置时，线段BM、DN和MN之间又有怎样的数量关系？请直接写出你的猜想.

选题意图：这是一道思路和方法同上的中考题，用来检查前面知识的掌握情况.

3.问题拓展，再探新知

教师出示幻灯片，学生探究（先只出示问题，不出示后面的解题提示）.

例3（2009年益阳市）如图8，在△ABC中，已知∠BAC=45°，AD⊥BC于D，BD=2，DC=3，求AD的长.

小萍同学灵活运用轴对称知识，将图形进行翻折变换，巧妙地解答了此题.

图8

请按照小萍的思路，探究并解答下列问题：

（1）分别以AB、AC为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点为E、F，延长EB、FC相交于G点，证明四边形AEGF是正方形.

（2）设AD=x，利用勾股定理，建立关于x的方程模型，求出x的值.

选题意图：这道题与前面两题在思路和方法上有革命性的改变，但却是基本图形的另一种变化，让学生了解图形的多变和内在的联系.

4.反馈练习，学以致用

教师出示幻灯片，学生练习.

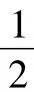
图9

（1）求∠BAC的度数.

（2）将△ACD沿AC折叠为△ACF，将△ABD沿AB折叠为△ABG，延长FC和GB相交于点H.求证：四边形AFHG是正方形.

（3）若BD=6，CD=4，求AD的长.

选题意图：这道题在基本图形的基础上，渗入了较简单的圆的知识，进一步说明利用基本图形改编试题是中考的常见形式.

5.小结提炼，知识建构

教师出示本课的图1，学生讨论，归纳小结，教师总结提升.

小结：（1）在正方形ABCD中，点E，F分别为DC，BC边上的点，则下列命题等价：①∠EAF=45°；②DE+BF=EF；③△CEF的周长等于正方形ABCD周长的一半.

（2）如AH⊥EF，已知EH和FH，则可求AH的长.

6.布置作业，内化提高

例5（2011年咸宁市）（1）如图10，在正方形ABCD中，△AEF的顶点E，F分别在BC，CD边上，高AG与正方形的边长相等，求∠EAF的度数.

（2）如 图 11，在 Rt△ABD中，∠BAD=90°，AB=AD，点M，N是BD边上的任意两点，且∠MAN=45°，将△ABM绕点A逆时针旋转90°至△ADH位置，连接NH，试判断MN，ND，DH之间的数量关系，并说明理由.

（3）在图10中，连接BD分别交AE，AF于点M，N，若EG=4，GF=6，BM=3，求AG，MN的长.

选题意图：这道中考题的内容紧扣本课的基本图形，思路和方法有一定的类比性，但又有一定的新颖性，作为课后作业，比较到位.

图10

图11

二、精彩课堂生成片段展示

片段1：（完成1.1（1）后）

教师：同学们都能根据提示完成此题，在完成此题的过程中，大家用到了正方形的什么知识？

学生1：正方形的两条边AB=AD.

学生2：两个角∠B=∠D=90°.

教师：很好，谁能把基本图形中正方形的条件简化吗？

学生3：老师，可不可以把正方形改为四边形，且AB=AD？

教师：不错！大家说行不行呢？

学生4：不行，因为旋转后点G，B，F不在同一条直线上！

教师：你总结得很好，你认为还需要什么呢？

学生4：∠B=∠D=90°.

教师：真聪明，现在大家能不能帮出卷老师出好第（2）小题，试试？

学生5：老师，∠EAF=45°不改吗？

教师：你怎么想到的，（装糊涂）我怎么没想到呢！大家说呢？

学生4：老师，要改！

教师：怎么改！

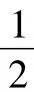
教师：你们真正了不起，大家看看出卷老师的第（2）小题.

片段2：（完成 1.2尝试应用，巩固提高后）

教师：同学们，刚才个个表现出色！这一课，我们是围绕基本图形展开的，现在老师出示另一道题，大家看看能不能解！（例2的题干，图12）

学生思考后，百思不得其解.

教师：这个图形和基本图形有关系吗？

学生目瞪口呆

教师：对比基本图形，大家看看有没有相似的地方！

图12

学生1：有角都等于45°.

教师：前面两题是通过旋转思想来解决问题，那么这一题大家能不能通过其他的全等变换把此图变为基本图形呢？

学生3：老师，不可能吗？相差太多啦！

学生4：老师，旋转是基本方法，轴对称也是，可是轴对称后的图形不是基本图形呀！

教师：（老师画出轴对称后的图形）你怎么想到轴对称的？

学生4：刚才第一题如果过点A作EF边上的高就和现在的图形差不多.

教师：老师为你的发现而高兴，你对初中的全等变换掌握得很到位，课后大家讨论看例1能不能这样做，现在其他同学帮助他想一想，与基本图形还差什么？

学生6：延长EB和FC交于点G，就变成基本图形.

教师：对呀！那么四边形AEGF是正方形吗？

学生5：老师，是正方形呀！

教师：真的吗？你怎么证明的呢？

学生5：（ 略）（其他同学恍然大悟，频频点头）.

教师：这说明这一道题确实与基本图形有关，且同学们想到了轴对称，了不起！可是与我们解决这一题还相差很远呢.再来，我们看谁先解出来！

学生4：（说出解法）（其他同学鼓掌）.

教师：我们的学生真是天才，我为我有这样的学生而高兴，刚才同学们解决问题的数学方法是什么？

全体同学：勾股定理列方程.

教师：同学们，初中数学代数是重点，方程是代数的核心，同学们可千万不要忘记！

下面请大家完成2009年益阳市中考题.

三、课后反思

1.问题呈现

例1的呈现不是一步到位，而是分步给出，克服以往的整体出示，让学生在老师的引导下步步深入，学会思考问题的方法，有利于学生弄清问题的实质.

例3的呈现更为大胆，学生看到问题后，根本没有思路.可学生却在老师的引导和自己的大胆猜想下，分层推进，渐渐深入，直至“庐山真面目 ”.

这种问题的呈现形式，向学生提出了挑战，他们在老师的引导过程中经历思考、合作和探究，使得学生思维的活跃度、参与度达到了一个新的高度.

2.问题安排

例2是一道思路和方法同例1的中考题，这样前后题有一定的联系，学生不需要理解考题的背景，降低审题成本，让学生在已建构的知识基础上，在同一个问题背景下思考，进行探究，抓住问题惯性，大大降低了学生在课堂上的审题成本.

例4也是一道思路和方法同例3的中考题，只是增加了圆的知识，而考查的内容和上一题几乎一样，让学生通过练习，达到做一题，会一类，通一片的效果，使学生更好地认清问题的本质，提高学生独立探究和解题能力.同时由于这道题学生认清问题的本质后，可以类比上一题的解法，抓住方法惯性，降低学生解题的时间成本.

3.课后巩固

这道中考题作为课后作业，能有效提高课堂教学效果，及时巩固课内所学知识.同时第（1）、（3）小题与基本图形息息相关，学生能抓住问题惯性降低审题成本；第（3）小题求AG的长与课堂方法一致，学生能抓住方法惯性降低时间成本.

另外中考专题复习阶段，学生时间紧、任务重.此题作为这节课的课后作业，学生的思维要远远低于其他时间布置，有效降低了学生的思维成本，却达到了较好的效果.

4.课堂结构

整堂课思路清晰，环环相扣，重难点突出，设计合理.学生既有类比学习的过程，又有大胆猜想的过程；既有学为所用的练习，又有知识内化的提炼；既有学生的灵感爆发，又有老师的点睛点拨.

5.课堂内容

在实施有效课堂教学，构建高效课堂的今天，中考专题复习课怎么办，是“老调重弹”，还是“老歌新唱”，答案是肯定的.只有我们老师树立全心全意为学生服务的思想，肯吃苦、肯钻研，一定能“老歌新唱”，唱出学生新的好奇心、新的发现、新的数学能力.本节课利用一个基本图形，唱出了初中数学的部分核心内容：旋转、轴对称、正方形、圆、勾股定理、方程；唱出了学生以简驭繁、审同辨异、同中观异的好思维.

四、结束语

中考专题复习课中，我们要牢固树立“成本意识”，抓住问题惯性、方法惯性和思维惯性，真正把学生当作学习的主体，改变教师的角色意识，全心全意为学生服务，充分利用课堂教学时间，尤其是课堂中学生的实用学习时间，既达到提高教学质量的目的，又达到真正“减负”的目的.当然，只有老师的“大成本”，才会有学生的“小成本”.

1.陆志强.换个角度看课堂教学成本.中学数学，2012，10.