基于核密度估计的点云鲁棒配准算法

林洪彬 刘 彬 张玉存

1.燕山大学，秦皇岛，066004

2.河北省测试计量技术与仪器重点实验室，秦皇岛，066004

0 引言

点云配准是计算机视觉领域的基本问题之一，广泛应用于距离数据融合、医学图像对准、目标定位、跟踪及识别［1］。ICP算法是经典的点云配准算法，然而，ICP算法存在如下不足：①代价函数的不可微性要求点云之间有足够的重叠区域，否则算法容易陷入局部极小；②ICP算法需要一个紧的初始条件。上述两点要求在应用ICP算法之前必须通过一定的预处理方法估计点云之间的重叠区域，并进行粗配准，以获得ICP算法的初始值。点云配准的难点在于异常值、背景和噪声等对配准精度的影响。为了消除上述因素对配准算法精度和鲁棒性的影响，文献［2－3］相继对ICP算法进行了改进。除此之外，人们还提出了两类方法对配准算法的鲁棒性进行改善。第一类方法通过对异常值、背景和噪声进行统计学建模，进而采用 ML/MAP估计的方法进行配准。如Hasler等［4］研究了图像配准中的异常值建模问题；Ying等［5］研究了基于统计模型的局部重叠对象识别问题。然而，这类方法的问题在于，在许多实际应用场合，对干扰因素的精确统计学建模是不可行的。第二类方法采用变换不变的鲁棒特征结合代价函数进行配准，以获得针对异常值、背景和噪声等干扰鲁棒性更好的配准算法。如Viola等［6］提出了一种基于融合信息的配准算法；Tsin等［7］提出了一种基于统计相关的鲁棒点云配准算法（KC算法）；Huttenlocher等［8］提出了一种基于局部Hausdorff距离的配准算法；Chui等［9］提出了一种基于混合模型的特征配准算法；Jian等［10］提出了一种基于高斯混合模型的鲁棒配准算法（GMM（gaussian mixture model）算法）等。杨静等［11］提出了一种基于简单Schur凹函数的图像配准测度；李晖等［12］提出了塔式分解和模糊梯度场的图像配准算法。这类算法的问题在于不同的代价函数和优化方法对算法性能影响较大。因此，设计合适的代价函数并根据代价函数的特点探寻全局合适的优化方法成为此类算法的关键，本文即属于此类方法。

本文基于核密度估计理论提出了一种新的测度函数，对不同参数下测度的性能进行分析，论证了利用该测度进行寻优配准时存在的局部极值现象和极值漂移现象。在此基础上提出了一种基于BFGS拟牛顿法的变尺度优化配准算法，解决了算法鲁棒性与配准精度之间的矛盾。

1 点云的核密度分布模型建立

设M＝｛mi，i＝1，2，…，Nm｝表示模型点云，S＝｛si，i＝1，2，…，Ns｝表示场景点云，两个点云可以视为对目标所对应的实向量空间Rd进行观测所得到的样本。

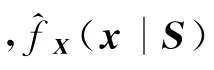
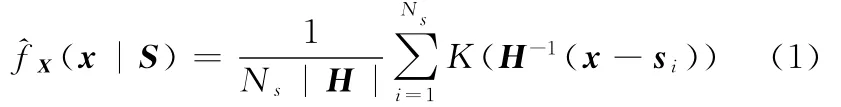
其中，H为d×d阶正定带宽矩阵，为简化计算，取H＝hId，Id为d×d阶单位矩阵；K：Rd→R为满足如下条件的非负核函数：

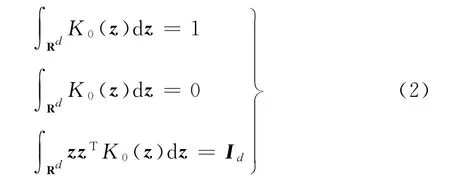
对于三维点云，d＝3。出于一般性考虑，选取高斯函数作为概率估计的核函数，即

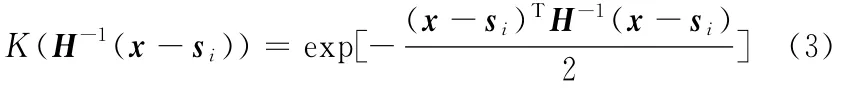
由此，可以通过上述过程分别建立离散点云M和S的连续核密度分布模型。

2 相似性测度的构造

核密度函数相似性测度对配准算法性能的提高具有重要作用，通常用于描述两个核密度分布相似性的测度有积分绝对值误差测度、Kullback－Liebler测度、MI（mutual information）测度、欧氏测度等［10］。不同的测度函数优化过程具有不同的鲁棒性和计算效率，如欧氏距离计算方便、意义明确，在相似性评价方面得到了广泛应用，但相比于Kullback－Liebler测度，其鲁棒性稍差。在文献［10］提出的GMM测度函数的基础上，本文提出了如下测度函数：

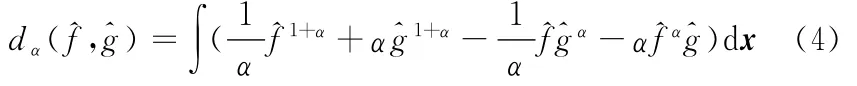
当α→0时，有

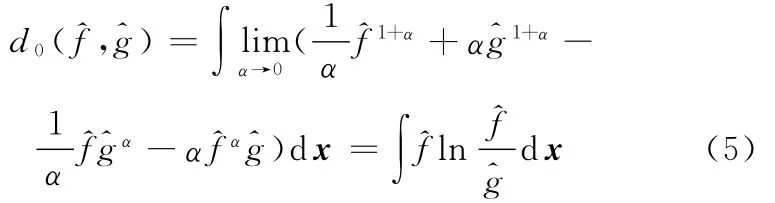
当α→1时，有

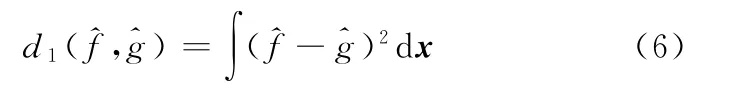
此时，d1（f，g）为与之间的欧氏距离。因此，利用本文提出的测度函数可以通过单一参数α可以调整算法的鲁棒性和渐进效率。

当配准对象为刚体时，空间变换矩阵T可以表示为：T（M）＝Rmi＋t，（i＝ 1，2，…，Nm），其中R为3×3阶旋转矩阵，t为3×1阶平移向量。此时，

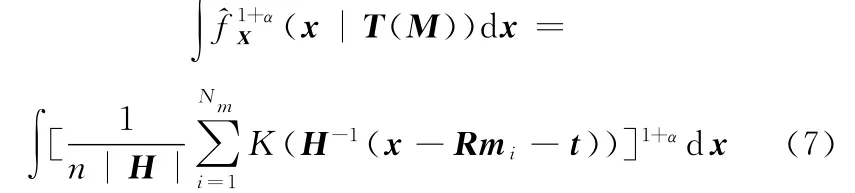
令x＝Rx′＋t，则

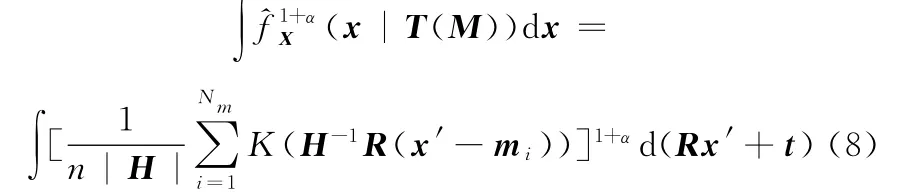
由式（3）可得

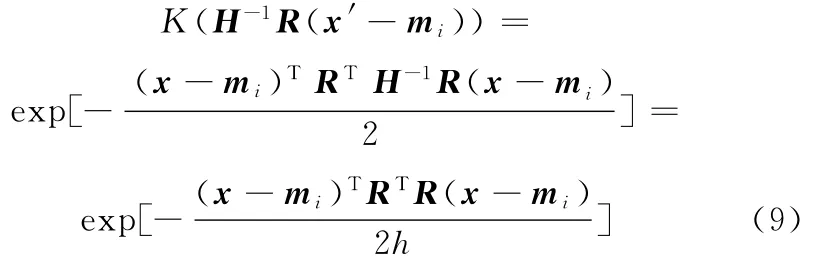
由于R为刚体变换矩阵，故，RRT＝I3，detR＝1，则

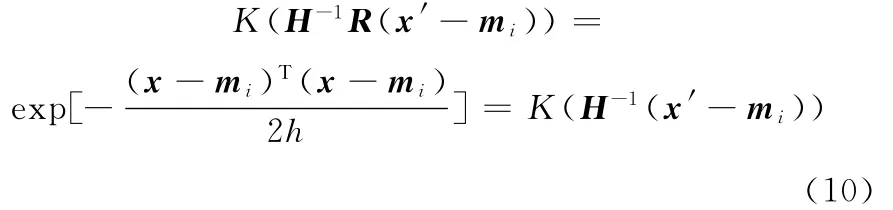
将式（10）代入式（8）可得

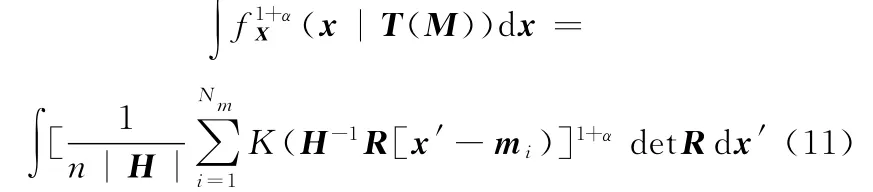
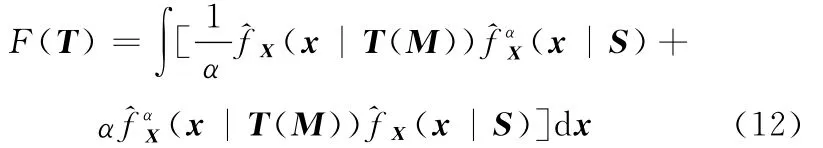
当α＝1时，测度函数F（T）的解析表达式为

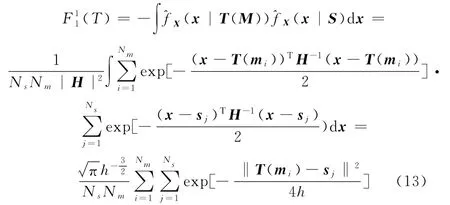
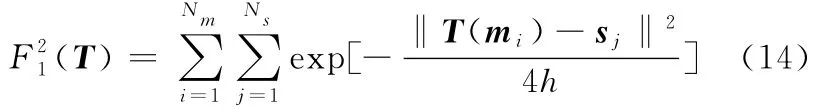
当α＝2时，测度函数F（T）的解析表达式为

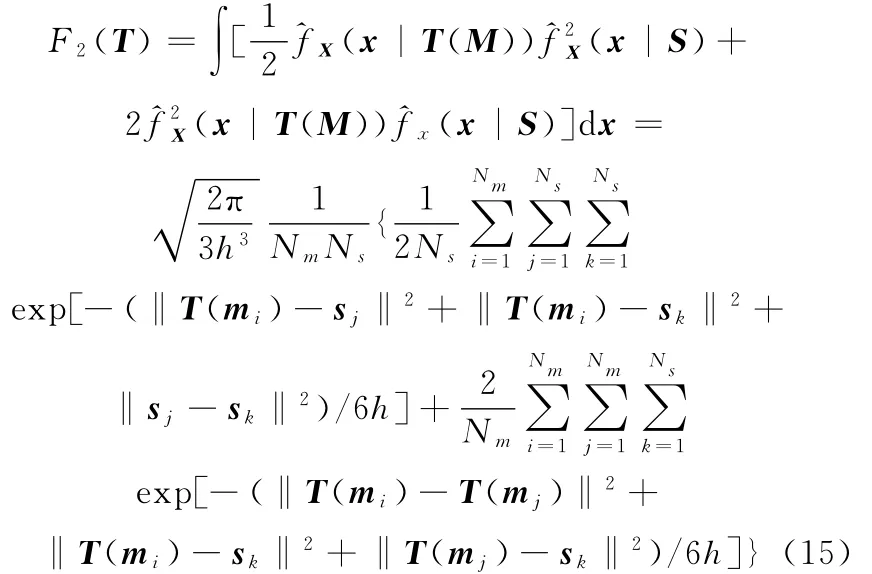
3 相似性测度的性能分析

首先，随机生成一个3×100的服从正态分布的随机矩阵作为场景点云M。其次，对场景点云M沿x轴方向平移3个单位，并随机选取其中50列作为模型点云S。h分别取0.1，10，20，50，100时，测度函数随偏移量tx的变化关系如图1所示（说明：本文除角度的量纲取（°）或rad，其他均为量纲一量）。再采用同样的方法测试测度函数对旋转参数的性能，设定模型点云和场景点云之间的旋转关系为θx＝π/3。此时，测度函数随旋转量θx的变化关系如图2所示。

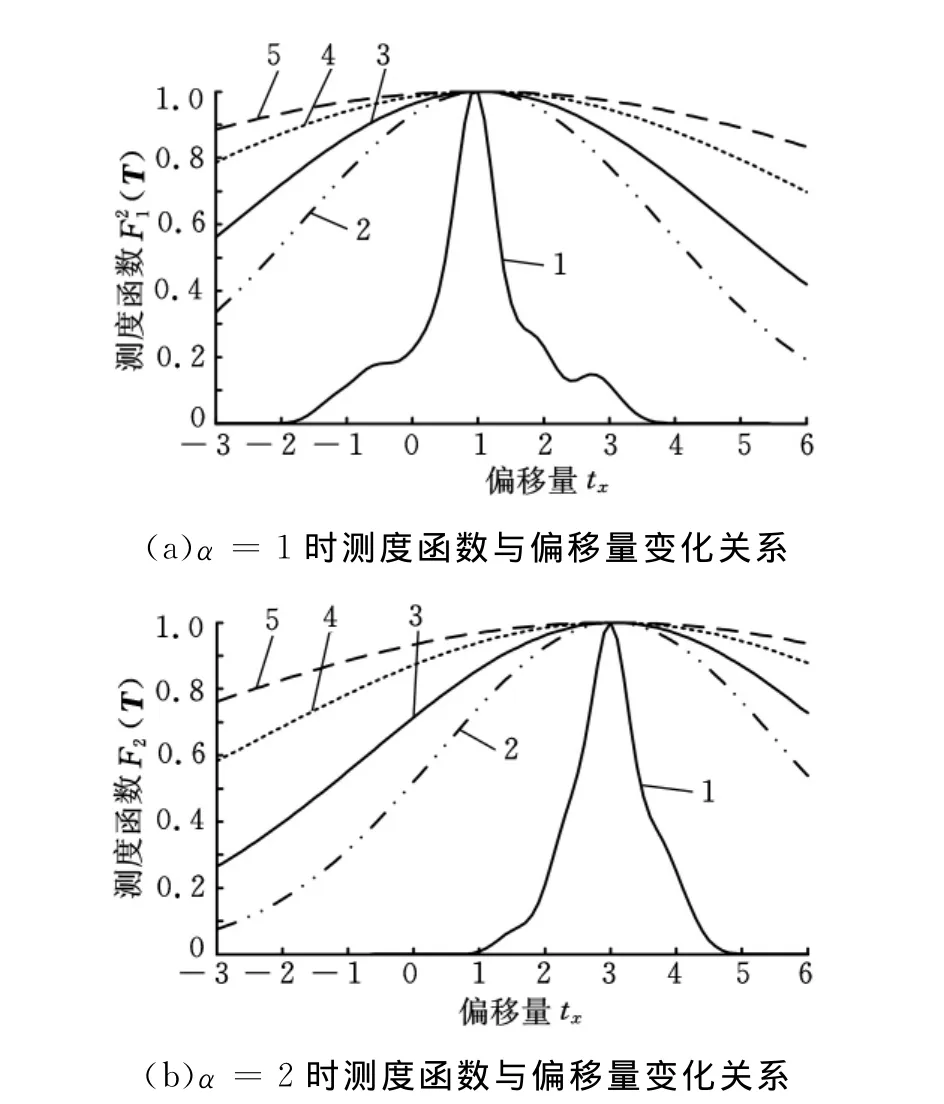
图1 不同参数下测度函数与偏移量tx关系曲线

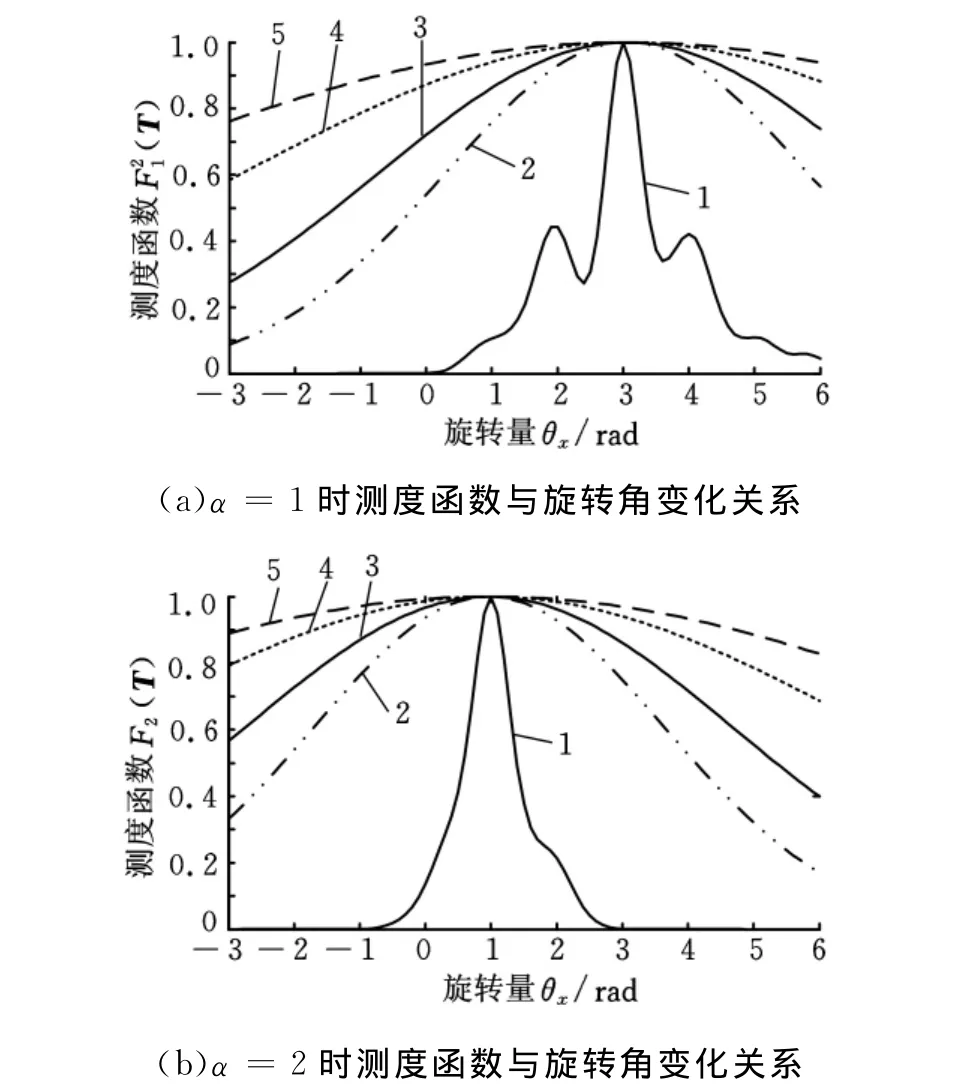
图2 不同参数下测度函数与绕x轴旋转角θx关系曲线

由式（14）可知，α＝1的情况下本文测度等价于文献［7］和文献［14］所采用的测度。图1表明，针对平移变换，通过搜索测度函数的极大值可以确定平移参量，实现点云的平移配准。图1a表明：α＝1时，尺度参数越大测度函数曲线越宽，曲线越光滑，峰值位置偏离真实值，采用大尺度参数的测度函数进行配准时将存在残余误差，我们把这种现象称为过尺度参数导致的极值漂移现象；尺度参数越小测度函数曲线越窄，曲线可能出现局部极值点，采用小尺度参数的测度函数进行配准时算法可能因陷入局部极小而导致失配，我们把这种现象称为欠尺度参数导致的局部极值现象。图1b表明，当选取α＝2时，测度函数曲线在极值漂移和局部极值方面性能更好，采用此测度函数的配准算法具有更好的鲁棒性和配准精度。图2表明，在进行旋转参数的配准时，选取参数α＝1也会导致极大值漂移和局部极值的问题，而选取参数α＝2可以改善这两种现象，提高算法的鲁棒性和准确性。

为了检验测度函数极值点的统计稳定性，将实验重复进行100次，统计各种测度函数全局极大值所在位置的均值μ和标准差σ，实验结果如表1和表2所示。

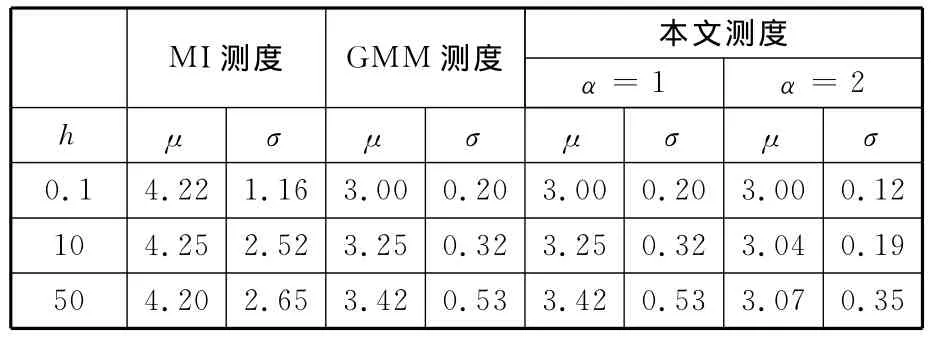
表1 测度函数对平移参数估计结果统计表

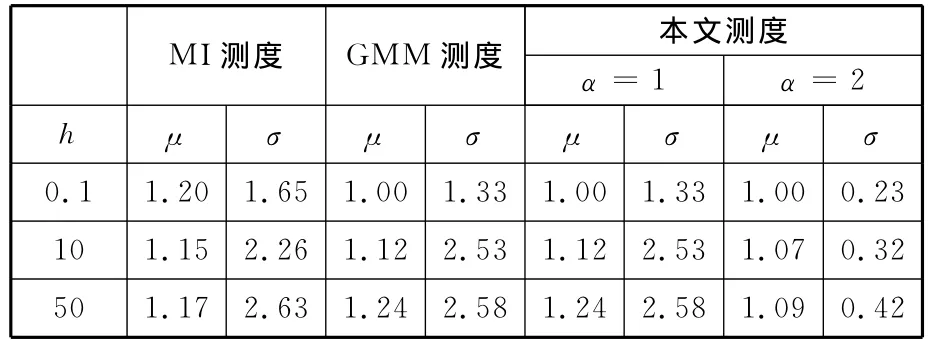
表2 测度函数对旋转参数估计结果统计

对比三种测度可以发现，与MI测度相比，本文提出的测度和GMM测度对于平移参数和旋转参数的估计均具有更好的准确性和有效性。通过对比GMM测度实验结果和本文测度实验结果可以发现，当α＝1时，本文测度的估计性能与GMM测度估计性能相同，而当α＝2时，测度对参数估计的性能优于GMM测度的估计性能。

4 基于BFGS优化的变尺度配准算法

通过表1和表2可以发现，应用本文提出的测度可以改善配准参数估计的准确性和有效性。然而，对比不同尺度参数下GMM测度和本文测度的性能可以发现，随着尺度的增大，对平移参数和旋转参数估计的偏倚现象明显，导致参数估计准确度降低。图1和图2也表明，尺度参数过小可能会导致局部极值现象的产生，从而导致点云失配。为此，本文提出了一种基于BFGS优化的变尺度配准算法，其优化过程如图3所示。

首先，随机选取初始参数T0作为极值点搜索的初始条件，同时，为了保证算法的收敛域和平滑性，选取一个较大的初始参数h0。再利用BFGS拟牛顿法搜索该尺度下测度函数极大值所在位置T1，在通过某种机制减小尺度参数h并以T1为搜索初始条件，获得T2依次类推，直至达到预定的配准精度。

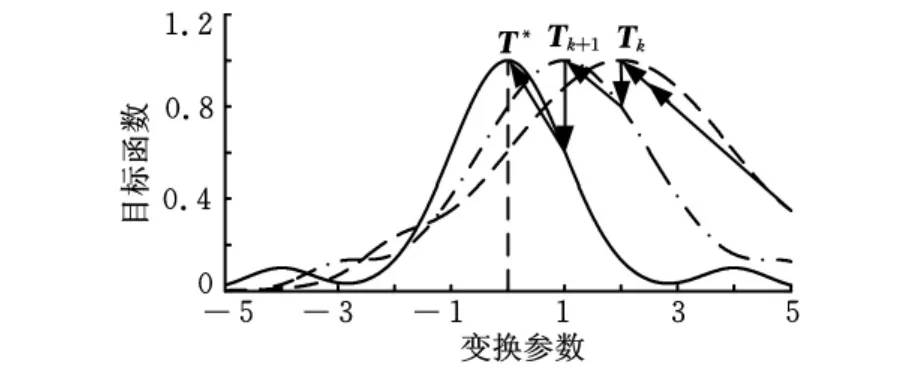
图3 变尺度优化过程示意图

基于BFGS优化方法的变尺度配准算法流程如下：

（1）初始化。h0＝3λmax和T0＝［00000 0］T，并令k＝0，其中，λmax为两个点云自相关矩阵的最大特征值，I4表示4×4阶单位矩阵。

（2）更新变换矩阵T。以Tk为初始条件，以hk为尺度，利用BFGS拟牛顿法搜索测度函数F（Tk，hk）的极大值。并将此极大值所在位置记为Tk＋1。

（3）更新尺度参数h。hk＋1＝μhk，选取μ∈（0.9，0.96），k←k＋1。

（4）循环步骤（2）、（3），直至 ‖Tk＋1－Tk‖ ＜ε。

采用这种衰减尺度的BFGS拟牛顿搜索法进行配准主要有三个优点：① 拓展了算法的收敛域；②克服了欠尺度参数导致的局部极值现象，减小了算法失配的可能；③克服了过尺度参数导致的极大值漂移现象，提高了配准精度。

5 实验研究

为了验证算法的性能，本节分别通过仿真信号和实测信号的配准实验对算法的可靠性和鲁棒性进行分析和比较。

5.1 受白噪声干扰点云配准实验（实验1）

（1）模型点云M的构造。通过如下公式构造一条三维空间曲线，并在该曲线均匀选取200个点作为模型点云M：

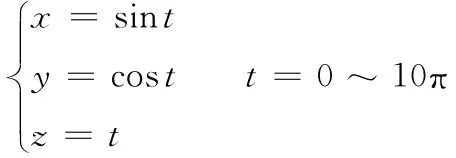
（2）场景点云S的构造。对模型点云M进行旋转和平移变换，变换参数

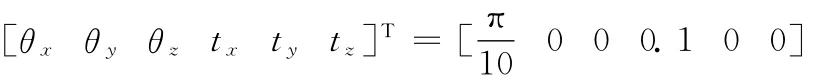
再增加信噪比为20dB的白噪声作为干扰，由此构造场景点云S。原始点云以及通过ICP、GMM和本文方法的配准结果如图4所示。

图4表明，在给定实验条件下ICP算法、GMM算法和本文算法均可实现点云的精确配准，说明这几种方法相对与白噪声干扰都具有鲁棒性。

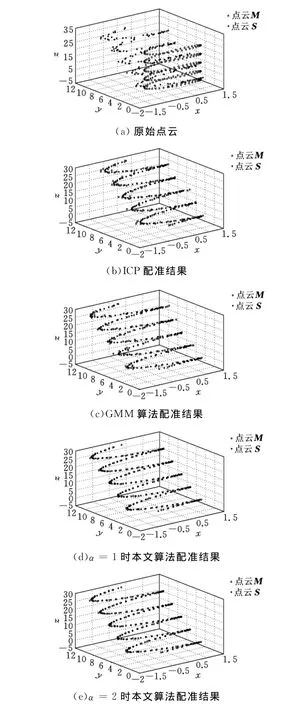
图4 带噪声点云配准实验结果

5.2 配准算法收敛性能实验（实验2）

为了检验算法的收敛性能，设计了实验2，实验中模型点云M的生成方法和实验1相同。在此基础上分别改变绕x轴方向转角θx∈（－π，π）和沿x方向平移tx∈（－20，20），并附加20dB白噪声作为场景点云S。分别用ICP算法，GMM算法和本文算法（α＝1，μ＝0.9）进行配准，求取各种算法的配准误差。配准误差随变换参数变化关系曲线如图5所示。

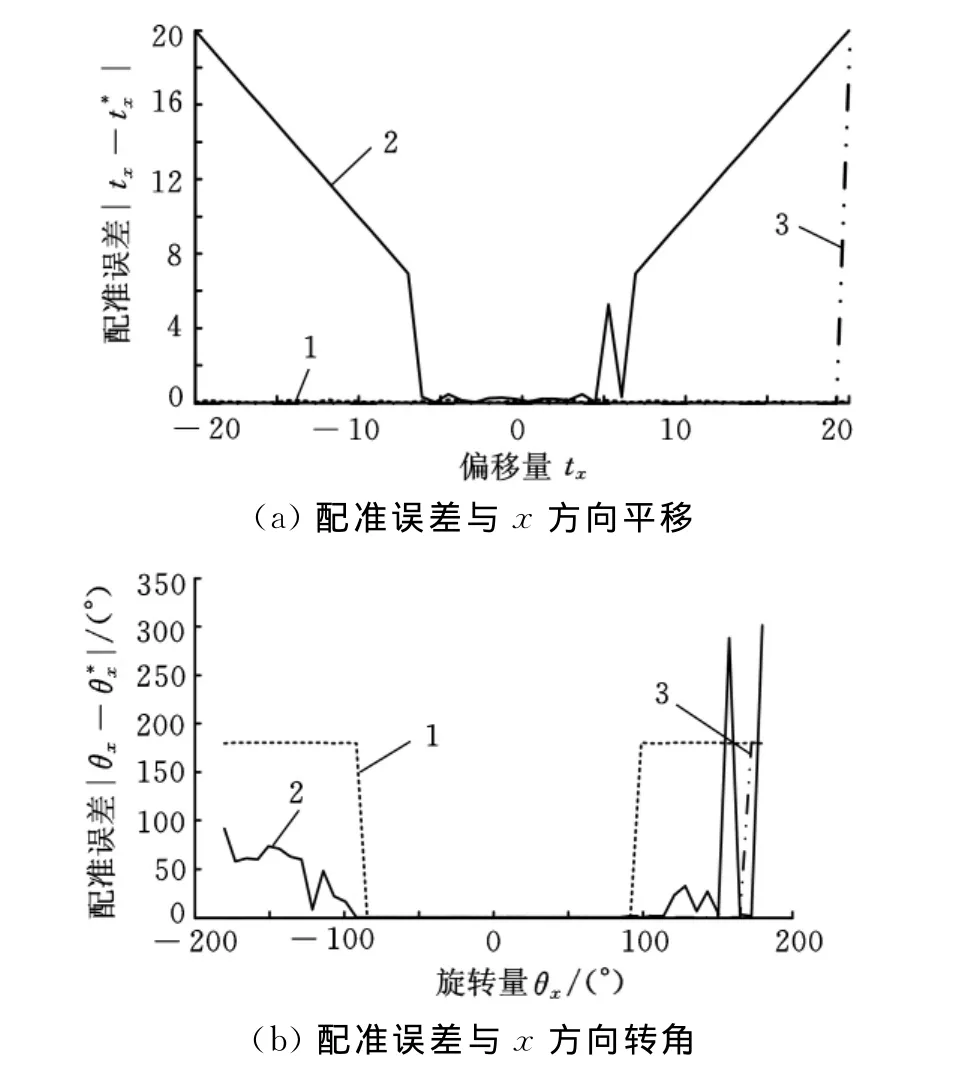
图5 配准误差随变换参数变化关系曲线

观察图5a可以发现，在针对单纯平移参数的配准中，ICP算法和本文算法在（－20，20）范围内可获得全局收敛的配准效果，而GMM算法的收敛范围为（－4.3，4.3）。这说明在处理单一平移参数的配准时，GMM算法要求两个点云之间的相对平移量较小，限制了算法的实际应用。由图5b可知，针对单纯旋转变换，ICP算法的收敛区 间 为（－85°，85°），GMM 算 法 的 收 敛 区 间为（－90°，105°），而 本 文 算 法 的 收 敛 区 间为（－180°，170°）。收敛区间越宽，说明使用该算法时两个点云之间的相对变换参数的允许范围就越大，从而算法的适用性就越好。综合分析图5可以发现，不论是针对旋转参数的配准还是针对平移参数的配准，相对于ICP算法和GMM算法，本文提出的算法都具有更好的收敛性能。

5.3 局部重叠点云配准实验（实验3）

为了验证点云局部重叠情况下本文算法与传统算法的性能，设计了实验3。实验原始数据为一组人脸激光扫描散乱点云，记为PtsFace，扫描点数NPtsFace＝392，点云PtsFace的坐标分布范围如下：（x×y×z）∈（［－1.18，1.11］×［－0.58，1.15］×［－1.82，2.56］）。取散乱点PtsFace的前80%的点作为模型点云M。再对PtsFace进行变换，参数［θxθyθztxtytz］T＝［π/5 0 0 0.2 0 0］T，取变换后点云的后70% 作为场景点云S。实验结果如图6所示。

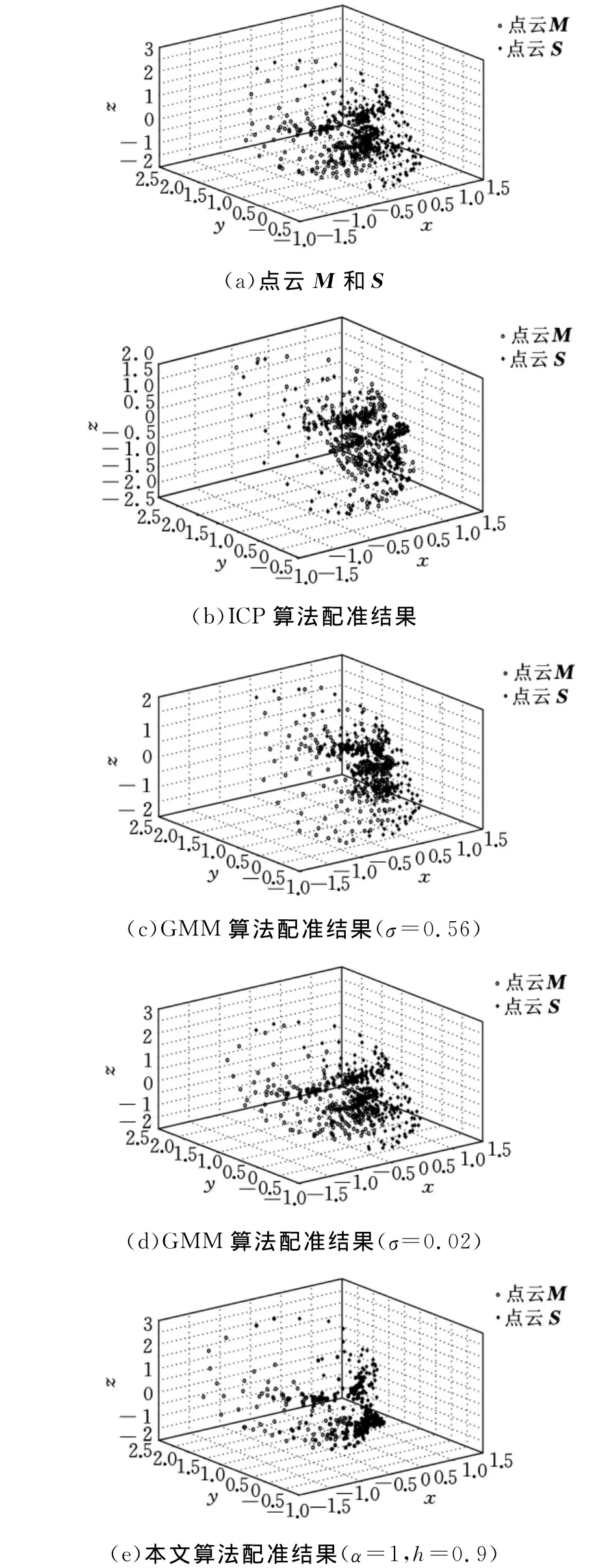
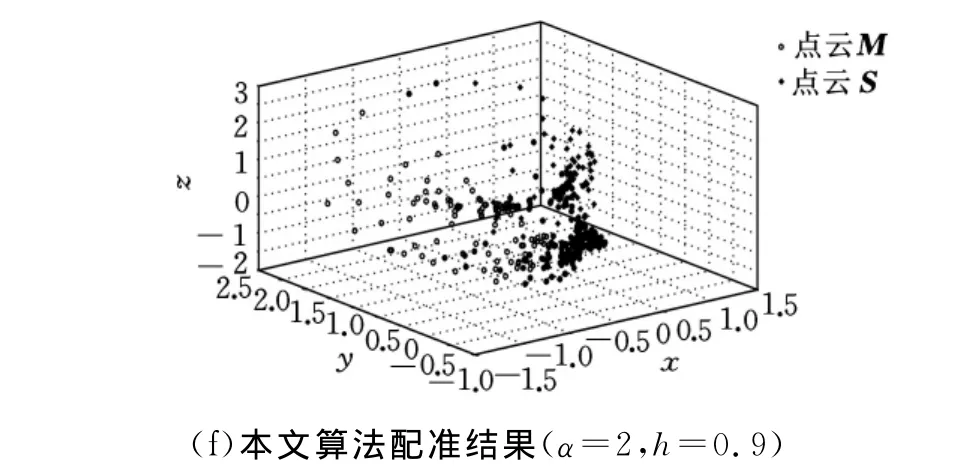
图6 局部重叠点云配准实验结果

图6表明，在给定实验条件下，ICP算法陷入局部极小，不能实现给定点云的配准。图6c表明，当参数选取为σ＝0.56时，GMM算法存在残余误差。由前面的理论分析可知，该残余误差是由过尺度参数引起的极值点漂移引起的，不能通过增加迭代次数和降低门限值的方法加以改善。

图6d表明，当参数选取为σ＝0.02时，GMM算法配准失败，由上文分析可知，这是由于欠尺度参数导致的局部极值现象所引起的，而这种现象主要存在于点云之间存在非重叠区域的情况。然而，在实际应用中点云之间往往存在明显的非重叠区域。因此，GMM算法在实际应用中也受到限制。图6e和图6f表明，本文方法可以实现具有非重叠区域点云的精确配准。

6 结束语

针对传统点云配准算法鲁棒性差、收敛区间窄的缺点，基于核密度估计的思想，提出了一种新的鲁棒的点云配准算法。本文从点云的概率分布模型建立入手，将点云配准问题表述为核密度函数相似性寻优问题，提出了用于描述核密度分布相似性的测度函数，研究了该测度函数的性能及其与其它测度函数之间的关系。针对算法实际应用中过尺度参数和欠尺度参数两种情况造成的配准残余误差和配准失败的情况，提出了一种变尺度BFGS寻优方法，实现了点云的鲁棒、精确配准。

［1］Salvi J，Matabosch C，Fofi D，et al.A Review of Recent Range Image Registration Methods with Accuracy Evaluation［J］.Image and Vision Computing，2007，25（5）：578－596.

［2］Fitsgibbon A W.Robust Registration of 2Dand 3D Point Sets［J］.Image and Vision Computing，2001，21（13/14）：1145－1153.

［3］Granger S，Pennec X.Multi－scale EM－ICP：A Fast and Robust Approach for Surface Registration［C］//In ECCV’02.London：Springer－ Verlag，2002：418－432.

［4］Hasler D，Sviaz L，Süsstrunk S.Outlier Modeling in Image Matching［J］.PAMI，IEEE Trans.，2003，25（3）：301－315.

［5］Ying Z，Castanon D.Partially Occluded Object Recognition Using Statistical Models［J］.International Journal of Computer Vision，2002，49（1）：57－78.

［6］Viola P，WellsⅢ W M.Alignement by Maximization of Mututal Information［J］.International Journal of Computer Vision，1997，24（2）：137－154.

［7］Tsin Y，Kanade T.A Correlation－based Approach to Robust Point Set Registration［C］//ECCV’04.London：Springer－Verlag，2004：558－569.

［8］Huttenlocher D P，Klanderman G A，Gregory A K，et al.Comparing Images Using the Hausdorff Distance［J］.IEEE Trans.Pattern Anal.Mach.Intell.，1993，15（9）：850－863.

［9］Chui H，Rangarajan A.A Feature Registration Framework Using Mixture Models［C］//IEEE Workshop on Mathematical Methods in Biomedical Image Analysis，Washington：IEEE Computer Society，2000：190－197.

［10］Jian B，Vemuri B C.A Robust Algorithm for Point Set Registration Using Mixture of Gaussians［C］//ICCV’05.Beijing，2005：1246－1251.

［11］杨静，胡顺波，刘常春，等.基于简单Schur凹函数的图像配准测度研究［J］.电子学报，2008，36（12）：2328－2332.

［12］李晖，彭玉华，尹勇.基于平移旋转不变的塔式分解和模糊梯度场的医学图像配准［J］.电子学报，2009，37（4）：854－859.

［13］Silverman B W.Density Estimation for Statistics and Data Analysis［M］.London：Chapman and Hall，1986：170－180.

［14］Boughorbel F，Mercimek M.A New Method for the Registration of Three－dimensional Pointsets：The Gaussian Fields Framework［J］.Image and Vision Computing，2010，28（1）：124－137.