一类带有deadline约束的作业车间提前/拖期调度问题研究

李海宁 孙树栋

西北工业大学，西安，710072

0 引言

以适时、适量、零库存为特征的JIT生产模式属于一类绿色、节能、低成本的生产方式。而提前/拖期（Earliness/Tardiness，E/T）调度作为支撑JIT生产的核心技术之一，现已成为车间调度领域的重要研究分支。E/T调度要求订单或零件在各自的交货期准时完工，提前或拖期完工都会产生相应的惩罚成本。如果订单或零件提前完工，则会产生零件成品库存成本；对于化学、食品、药品等时效性较强的产品，过早完工则会产生变质、失效、挥发或产品性能退化等问题；另外，订单或零件的拖期完工则会打乱整个制造链的生产节拍，使得下游生产环节出现整机配套缺件、停工待料、设备闲置等诸多问题。因此，关注订单或零件的交货期，以满足订单或零件的准时化交付为目的，通过E/T调度来实现制造车间的精细运作和低成本运营，对于改善目前离散制造企业存在的高投入、低产出、低利润率等问题具有一定的现实意义。

文献［1－2］将车间E/T调度问题归结为单机E/T调度和多机E/T调度两类，并指出现有研究主要集中在单机E/T调度领域，针对多机E/T调度问题的研究相对较少；在多机E/T调度研究方面，大多又侧重于并行机调度，而对于经典的作业车间调度研究相对更少。在作业车间E/T调度相关研究中，文献［3］针对带有释放期和交货期约束的Job shop调度问题，以最小化总加权拖期成本为目标函数，采用基于邻域搜索的遗传算法进行求解，但其目标函数中未考虑提前成本这一指标；文献［4］针对动态装配型Job shop的提前/拖期调度问题，采用一种惩罚加权系数呈阶梯分布的分配求解规则，但这种基于规则的求解方法存在优化性能不足的问题；文献［5］基于模糊控制和遗传算法，提出求解Job shop提前/拖期问题的联合算法，但调度模型并没有涉及提前/拖期的惩罚系数的差异性；文献［6］将作业车间E/T调度转化为约束优化问题，并运用约束满足方法进行求解。

本文在现有E/T调度模型的基础上，添加了零件可接受的最晚完工时间（即deadline）约束条件，形成了一类带有零件deadline约束的作业车间E/T调度问题（以下简称E/T/D调度问题）。在车间实际生产中，零部件拖期在所难免，但受下游整机装配或客户订单的容许拖期范围限制，零件拖期不能突破零件的deadline，一方面，一旦零件交付延迟于deadline时限，则会导致下游整机装配出现严重拖期或客户拒收等重大损失；另一方面，在企业与客户进行订单交货期协商的过程中，企业利用订单或零件的deadline来评估客户订单的可行性，可以事先避免因订单交货期设置不合理而导致的客户信誉受损、丢失客户等问题。

在E/T调度中引入零件deadline约束后，即可形成一类零件交货期窗口，即零件的交货期和deadline之间的交货期容许范围。如果零件在该交货期窗口内完工，则会产生拖期惩罚成本；如果零件实际完工时间突破该交货期窗口，则调度结果被视为非法解。这种带有硬约束的交货期窗口和文献［7－8］提出的交货期窗口存在本质差异，文献［7－8］中的交货期窗口实质上属于一类软约束，即如果零件在此交货期窗口内完工则不受惩罚；若零件拖期完工则产生拖期惩罚成本，但并不会产生非法调度解。因此，这类带有交货期窗口硬约束的作业车间E/T调度问题对零部件交货期的控制更为严格，也更符合JIT对准时制生产的管理理念，它适用于对交货期控制严格的诸如军工类、外贸类和配件供应类制造企业或生产车间。

将零件deadline约束条件引入作业车间E/T调度问题后，调度算法设计面临的首要问题是如何避免因零件完工时间违反deadline约束而出现非法调度解；另外，在满足零件deadline约束的前提下，接下来面临的主要问题就是如何降低E/T调度总成本。为此，本文提出了一种改进型遗传算法（enhanced genetic algorithm，EGA），以期解决这类对交货期控制更为严格的作业车间E/T调度问题。

1 作业车间E/T/D调度模型

对于作业车间E/T/D调度问题而言，其调度任务是指在满足工艺路线、机床能力、零件释放期和零件deadline等约束的前提下，合理安排承制零件在各机床上的加工序列和开工时间，使得提前/拖期总惩罚成本最小。

1.1 相关变量说明

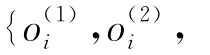
相关变量说明如下：rdi为零件Ji的释放期；di为零件Ji的交货期为零件Ji的deadline（即可接受的最晚交货时间），在同一零件Ji内，rdi为零件Ji的开始加工时间；Ci为零件Ji的加工完成时间；αi为零件Ji的单位提前惩罚系数；βi为零件Ji的单位拖期惩罚系数；为工 序的加工时间为工序的开工时间；为工序的完工时间，）为工序的承制机床

1.2 数学模型

该问题的数学模型描述如下：其中，式（1）为目标函数，使得整个调度任务集的提前/拖期惩罚总成本最小化。式（2）为零件Ji的提前惩罚成本。式（3）为零件Ji的拖期惩罚成本。式（4）为工艺路线约束，即同一零件Ji内两道相邻工序之间的时序关系约束。式（5）为机床能力约束，即同一承制机床上加工工序队列的时序关系约束。式（6）为零件释放期约束，即Ji的开工时间不应早于其释放期rdi。式（7）为零件deadline约束，即Ji的加工完成时间不能迟于该零件的。由式（7）可知，零件Ji的交货期容许范围为［］。若di＜Ci≤di，则Ji产生拖期惩罚成本；若Ci＞，则因Ji违反零件deadline约束而出现非法调度解。

2 改进型遗传算法设计

针对作业车间E/T/D调度模型，在标准遗传算法框架内，重点对解码操作进行了改进，形成了图1所示的EGA求解框架（包含EGA算法的伪代码和染色体解码过程两部分）。在EGA算法设计中，染色体编码采用基于工序的编码方法［9］；初始种群完全随机产生；选择操作采用精英保留策略和锦标赛方法［9］；交叉操作采用文献［10］提出的POX交叉算子；变异操作采用逆转变异方法［9］。

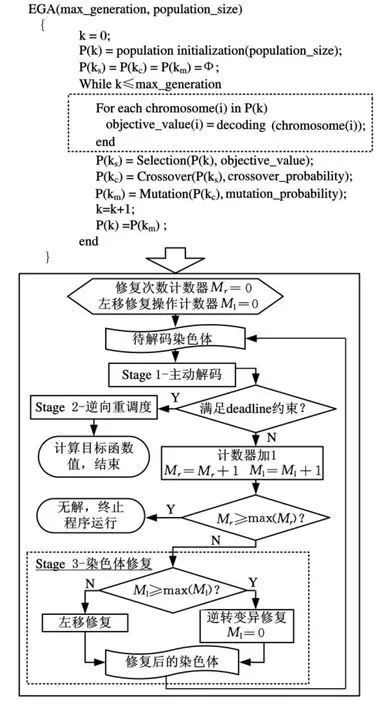
图1 EGA求解框架

在车间实际生产中，零件拖期会带来诸如整机装配延迟、订单损失和企业信用度降低等弊端，因此，相对提前问题而言，拖期问题更为严重。首先，零件不拖期或少拖期可以避免或者减小发生违反零件deadline约束的概率，因此，如何减少零件拖期是求解E/T/D调度问题首先需要解决的问题；然后，在零件拖期严重导致违反deadline约束时，如何通过算法内部的修复机制来及时调整调度结果以尽可能满足deadline约束，是E/T/D调度问题有别于传统E/T调度问题的特殊之处；最后，在满足deadline约束条件下，如何在降低零件拖期惩罚成本的基础上，进一步压缩零件提前惩罚成本，从而最终保证提前/拖期总惩罚成本最低，这是求解E/T调度问题区别于传统正规性能指标调度问题的关键所在。

基于以上三个问题的分析，同时为了降低E/T调度问题求解的复杂度，在设计EGA算法时，采取了拖期优先的调度策略，即将E/T/D调度问题分解为拖期子问题、修复子问题和提前子问题，并将一个染色体的解码过程划分为主动解码、染色体修复和逆向重调度三个阶段。

（1）拖期子问题。基于拖期优先的调度策略，可以将非正则性能指标的E/T调度问题转化为正规性能指标的拖期调度问题。文献［11］指出：对于正规性能指标的调度问题，最优调度解必在主动调度集中。因此，针对这类拖期调度子问题，采用主动解码方法［11］得到主动调度结果，以此来降低拖期惩罚成本，同时可以降低违反deadline约束的发生概率。

（2）修复子问题。针对第一阶段主动解码中出现的违反deadline约束的染色体，采用左移修复和逆转变异［9］相结合的染色体修复方法来调整问题染色体的基因序列，以促使修复后的染色体满足deadline约束条件。

（3）提前子问题。在主动解码得到的主动调度结果的基础上，针对提前子问题，第三解码阶段采用逆向重调度方法，促使第一阶段的主动调度结果尽可能向零件的各自交货期靠拢，以期在保持已有零件拖期成本不变的基础上进一步压缩提前惩罚成本。

下面针对EGA算法中的染色体修复和逆向重调度两部分进行重点阐述。表1所示的调度算例用来辅助说明操作算子。

表1 调度算例

2.1 基于关键路径的染色体修复方法

在初始种群和经过交叉、变异等操作产生的新种群内，因deadline约束的存在，在染色体解码过程中有可能产生非法调度解。为此，在EGA算法设计中，一旦解码过程出现非法解，则立即中断当前主动解码操作，并转入染色体修复环节。

染色体修复操作包括定位产生非法解的源头和修复问题染色体两个环节。非法解的源头定位通过临界工序和关键路径来进行筛选和过滤；修复操作则通过染色体修复方法来完成。如果染色体修复成功，即产生满足E/T/D调度模型全部约束的新染色体，则用新染色体替换种群中的原不可行染色体。

定义1 临界工序是指在解码过程中，导致其所属零件违反deadline约束所对应的当前工序。

定义2 关键路径是由临界工序依据“首尾相抵”原则逆向组成的工序链。

在关键路径｛o1，o2，…，ol｝中，ol为临界工序，o1为依据零件释放期开工的工序，“首尾相抵”的原则 是 指 满 足stl＝stl－1＋pl－1，stl－1＝stl－2＋pl－2，…，st2＝st1＋p1；另外，若ok∈ ｛o1，o2，…，ol｝，oi和ok均属于同一零件，oj和ok由同一机床加工，且满足（stk＝sti＋pi）∧ （stk＝stj＋pj），则选择oi作为关键路径上的工序。

定义3：关键块是指在关键路径｛o1，o2，…，ol｝内，满足sti＝sti－1＋pi－1（1＜i≤l），且在同一台机床上加工的工序所组成的工序集。

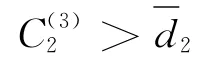
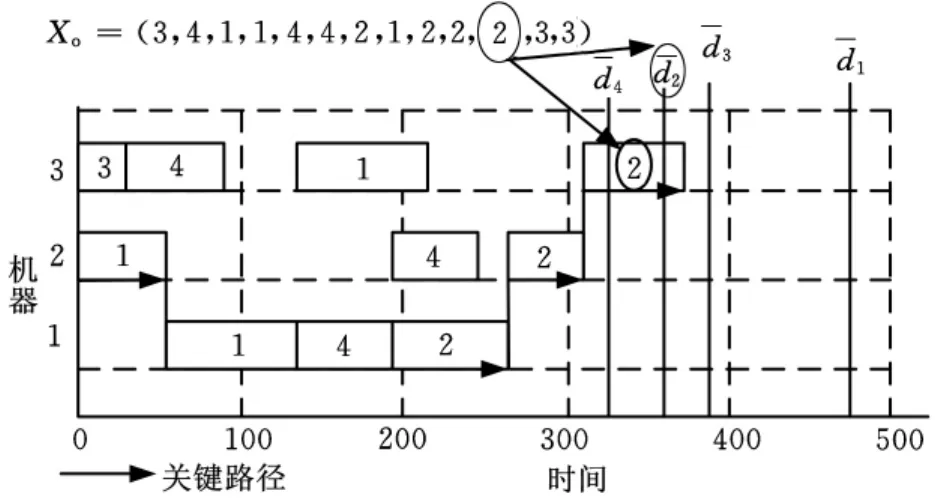
图2 关键路径和关键块示例

识别出非法解产生源头后，若执行左移修复操作的次数Ml没有超出其上限值max（Ml），则继续执行左移操作；否则，执行逆转变异［9］修复操作以大幅度更改染色体基因特征。

左移修复操作是将在关键路径上的临界零件的工序尽量向左移动，使得临界零件在其deadline之前完工。若某个块Bi中有临界工件工序u，JP［u］为工序u的工件前续工序，v为块Bi中位于u左侧的工序；Cv和CJP［u］分别为工序v和JP［u］的完工时间；由满足Cv≥CJP［u］的工序v组成集合V。左移操作的具体步骤是遍历关键路径上的所有块，若某块中有临界工件工序u，且V≠∅，那么任选一个v∈V，将u移动到v的左侧。

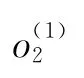
图3 修复后的染色体主动解码结果

2.2 逆向重调度

实际上，在保持第一解码阶段拖期成本不变的基础上，延迟零件和工序的开工时间有助于降低提前惩罚成本。为此，在EGA算法设计中，引入逆向重调度方法，具体计算步骤如下：

（1）确定逆向重调度的坐标原点。染色体完成解码后，对于提前完工的零件集E＝｛Ji｜Ci≤di｝，选择其交货期最大值me；对于拖期完工的零件集T＝｛Ji｜Ci＞di｝，选择其完工时间的最大值mt，取坐标原点为Or＝ max（me，mt）。

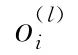
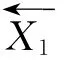
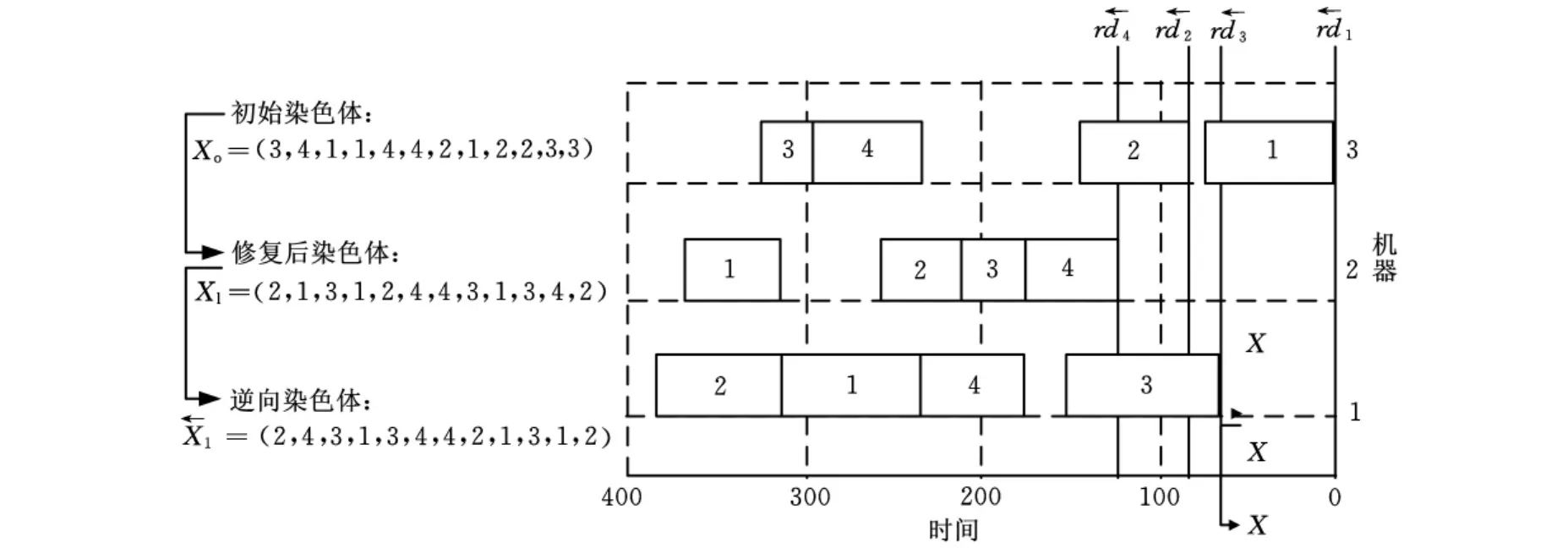
图4 逆向重调度结果

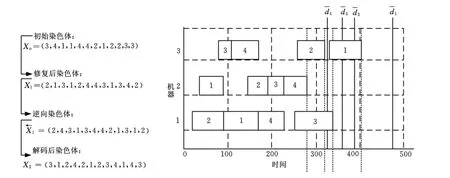
图5 解码最终结果

3 仿真实验

为了测试EGA算法性能，选择混合整数规划（MIP）方法和EGA算法进行比较。EGA通过MATLAB 7.0编程实现，利用 FICOTMXpress软件对上述E/T/D调度模型进行MIP求解。二者都在1.73GHz、1.0GB RAM 的计算机上运行。时间阈值为1200s，即当求解某个调度子问题的计算时间超过1200s时，则认为该调度问题无解。

3.1 调度用例

在文献［12］构造的算例基础上，本文通过调整问题规模、交货期松弛度和deadline松弛度产生18组参数组合，每个参数组合随机生成10个调度子问题，则共有180个调度问题作为测试用例。

（1）调度问题规模n×m分别为10×10、15×10和20×10。

（2）每个零件随机遍历所有机器，加工时间在［1，99］间随机产生。

（3）所有零件的释放期为0。

（4）各零件交货期在［0.75tlblf，1.25tlblf］区间内随机产生。其中，tlb为零件的完工时间下限值，由文献［13］中的公式计算得到；lf∈ ｛1.3，1.5｝为交货期松弛度。

（5）零件Ji的deadline为di＝ddi，其中，d∈｛1.0，1.2，1.4｝为deadline松弛度。

（6）提前惩罚系数和拖期惩罚系数在［1，20］区间内随机产生。

因此，3个问题规模、2个交货期松弛度、3个deadline松弛度，共同构成18种参数组合，采用N－M－lf－d标记一种参数组合。

EGA算法的参数设置如下：种群规模为50，最大迭代次数为100，交叉概率为0.9，变异概率为0.1，锦标赛选择算子中的竞赛规模K从｛2，3｝中随机选取，最大修复次数max（Mr）＝10000，左移修复操作的上限次数max（Ml）＝200。

3.2 评价指标

①有解数。每组10个调度子问题中，在1200s内求得调度解的个数。

②平均计算时间。每组10个调度子问题计算时间的平均值，无解子问题以1200s参与计算。

③最小成本值。每组10个调度子问题中，有解子问题对应的提前/拖期调度总成本的最小值，用以评测调度算法的寻优能力。

④平均成本值。每组10个调度子问题中，有解子问题的提前/拖期调度总成本的平均值，用以评测算法在某类调度环境下的搜索能力。

⑤平均空闲时间。每组10个调度子问题中，各零件最后两道工序之间的空闲时间的平均值，用来评测调度结果的均衡性。

⑥平均流动时间。每组10个调度子问题中，所有零件流动时间的平均值。

3.3 仿真结果及分析

EGA和MIP的实验结果见表2，表2中的N/A表示在限定时间1200s内算法未得到调度解。图6、图7所示分别为两种算法在平均空闲时间、平均流动时间两个指标方面的比较结果。

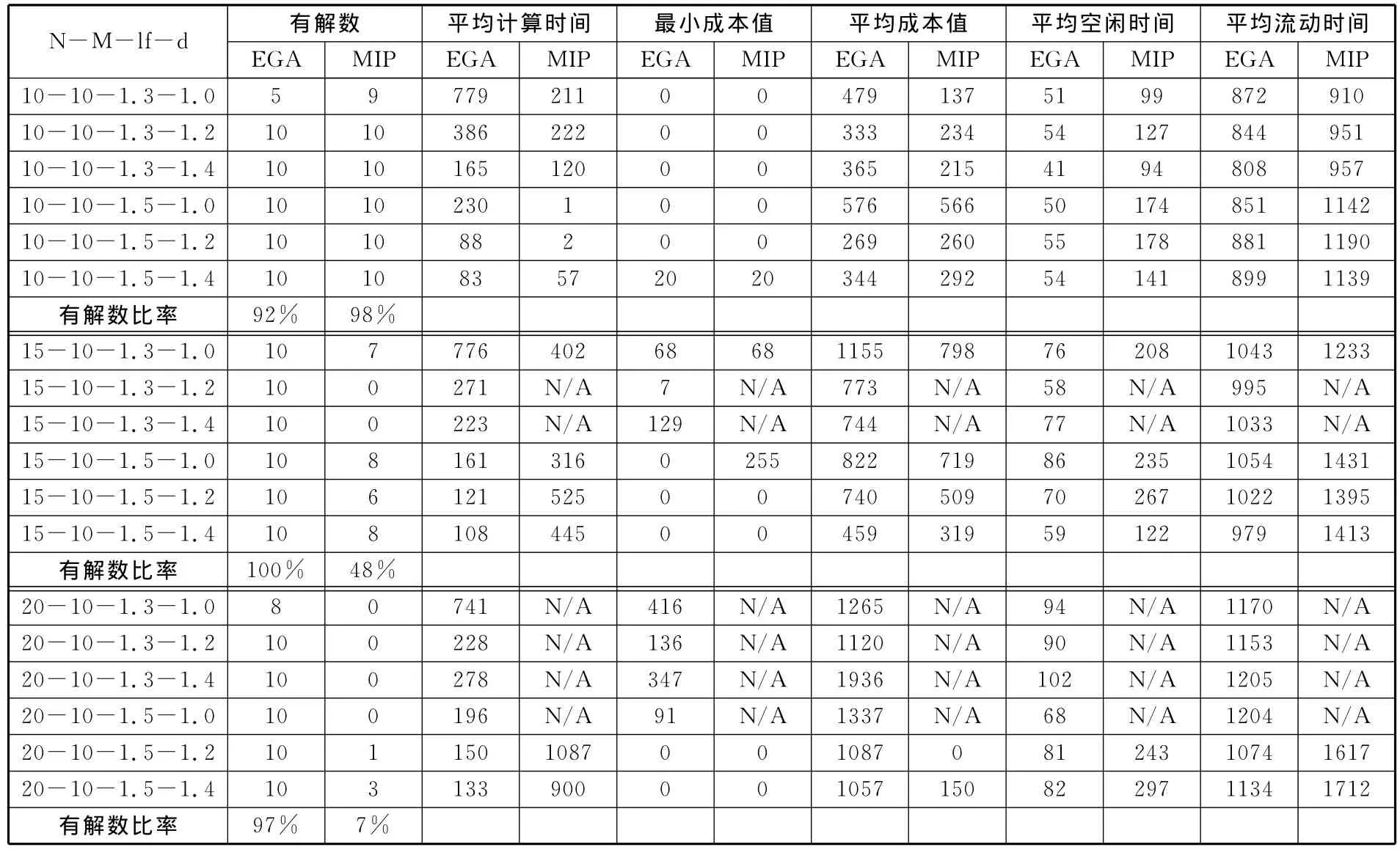
表2 仿真实验结果

由表2可知，除较小规模10－10－1.3－1.0组算例外，EGA算法在每组算例中的有解数均优于MIP方法；尤其当调度问题规模逐渐增大时，EGA解决问题数的优势愈加明显。在限定的1200s内，MIP方法在180个算例中只取得了92个算例的调度解，这是因为MIP方法的计算代价随着调度问题规模的增大而呈指数增加，导致MIP方法在限定时间内解决问题数量相对较少。从最小成本值指标来看，EGA算法和MIP方法在较小规模算例上取得的最优值一致，由于MIP方法属于一类数学优化方法，而EGA算法能取得与这类精确数学方法同样的结果，证明EGA算法同样具有搜索到最优解的能力。

对比图6和图7可知，在平均空闲时间和平均流动时间两项指标方面，EGA算法均优于MIP方法，这得益于在染色体解码过程中引入了逆向重调度方法，使得调度结果尽可能右移并接近零件的各自交货期，从而使得零件中间工序之间的等待时间大大缩短。

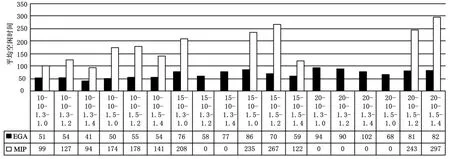
图6 EGA/MIP在平均空闲时间指标下的比较结果

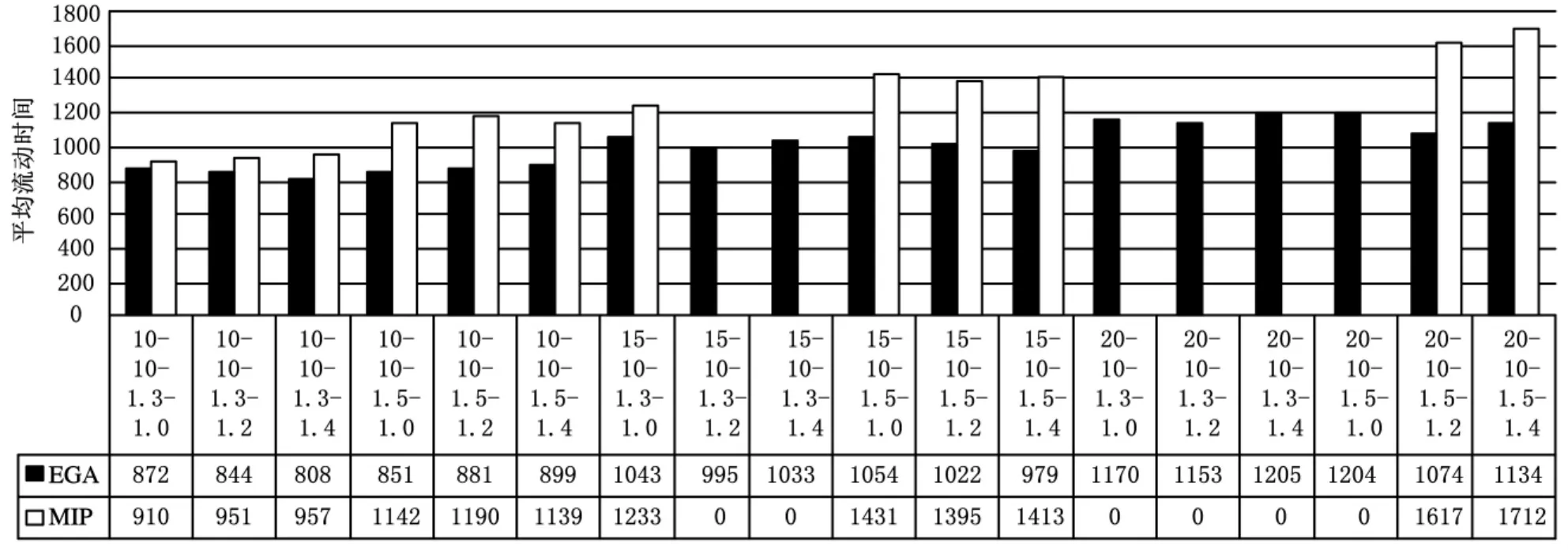
图7 EGA/MIP在平均流动时间指标下的比较结果

4 结论

本文在传统E/T调度问题的基础上，引入零件deadline时间约束条件，形成了带有零件deadline约束的作业车间E/T/D调度问题，这类问题的求解有助于解决目前E/T调度中存在的零件拖期没有上界的问题，同时有利于评估订单交货期的可行性，从而避免因零部件或订单交付严重拖期而导致的订单拒收、信誉受损等问题。

针对E/T/D调度问题，采取拖期优先的调度策略，将这类非正规性能指标的调度问题转化为拖期子问题、修复子问题和提前子问题，并在染色体解码过程中分别采用主动解码、染色体修复和逆向重调度三种方法，以此实现在满足零件deadline约束条件下尽可能降低提前/拖期惩罚总成本的目的。最后采用调度问题规模、交货期松弛度和deadline松弛度三个参数可调节的共计180个调度实例进行了仿真实验，实验结果表明，EGA算法在解决问题数、寻优能力、调度结果的均衡性等方面具有一定的优势。

［1］Lauff V，Werner F.Scheduling with Common Due Date，Earliness and Tardiness Penalties for Multimachine Problems：A Survey［J］.Mathematical and Computer Modelling，2004，40（5/6）：637－655.

［2］Sen T，Sulek J M，Dileepan P.Static Scheduling Research to Minimize Weighted and Unweighted Tardiness：A State－of－the－art Survey［J］.Int.J.Production Economics，2003，83（1）：1－12.

［3］Essafi I，Mati Y，Stephane D P.A Genetic Local Search Algorithm for Minimizing Total Weighted Tardiness in the Job－shop Scheduling Problem［J］.Computers ＆ Operations Research，2008，35（8）：2599－2616.

［4］Thiagarajan S，Rajendran C.Scheduling in Dynamic Assembly Job－shops to Minimize the Sum of Weighted Earliness， Weighted Tardiness and Weighted Flowtime of Jobs［J］.Computers ＆ Industrial Engineering，2005，49（4）：463－503.

［5］姚伟力，杨德礼，胡祥培.Job－shop提前/拖期调度问题的研究［J］.控制与决策，2000，15（3）：322－324.

［6］Sadeh N.Micro－boss：A Micro－opportunistic Factory Scheduler［J］.Expert Systems with Applications，1993，6（3）：377－392.

［7］刘兴初，赵千川，郑大钟.用GA算法解不同交货期窗口下的E/T调度问题［J］.清华大学学报（自然科学版），2000，40（7）：59－62.

［8］黄德才，朱艺华，王万良.带公共交货期窗口的提前/拖期非等同多机调度问题［J］.系统理论与实践，2001（4）：64－69.

［9］王凌.车间调度及其遗传算法［M］.北京：清华大学出版社，2003.

［10］张超勇，饶运清，李培根，等.基于POX交叉的遗传算法求解Job－Shop调度问题［J］.中国机械工程，2004，15（23）：2149－2153.

［11］Baker K R.Introduction to Sequencing and Scheduling［M］.New York：Wisely，1974.

［12］Beck J C，Refalo P.A Hybrid Approach to Scheduling with Earliness and Tardiness Costs［J］.Annals of Operations Research，2003，118（1/4）：49－71.

［13］Taillard E.Benchmarks for Basic Scheduling Problems［J］.European Journal of Operational Research，1993，64（2）：278－285.