浅谈FLAC3D在边坡动力稳定性中的应用

刘小焕，裴娜娜，韩晶晶，李 琳

(1.巴州基安岩土工程勘察设计有限责任公司，新疆库尔勒841000;2.陕西省高速机械化工程有限公司，陕西西安710075;3.西华大学建筑与土木工程学院，四川成都610039)

边坡受到的动力荷载主要来自地震、爆炸和机械振动等，所造成的破坏最多、最大当属地震荷载。地震荷载可能诱发山体滑坡，导致人员伤亡。展开地震荷载作用下边坡的地震反应、动力稳定性及工程安全性的研究，对于减小地震荷载诱发的灾害，确保工程的安全，保障国家基础设施建设，具有极其重要的经济和社会价值。

分析边坡稳定性问题，基本上有两种方法:极限平衡法和数值分析方法。目前，在岩土工程中，对边坡稳定性分析常用的数值分析方法有界面元法、拉格朗日元法、离散单元法、自适应有限元法和有限元法[1]。近年来，随着计算机技术的飞速发展，有限差分法以其独特的计算风格和计算流程在数值方法家族中异军突起，FLAC(Fast Lagrangian Analysis of Continua连续介质快速拉格朗日分析)就是岩土工程数值分析软件的典型代表。用极限平衡法，在开始分析时估计圆形破坏线的位置是必要的，而在FLAC中则不必要，FLAC将会通过直接模拟材料性能找到破坏面和破坏机理[2]。本文利用FLAC3D软件在边坡工程中的应用作了一些分析。

FLAC3D是二维计算程序在三维空间的扩展，用于模拟三维土体、岩体或其他材料力学特性，尤其是达到屈服极限时的塑性流变特性，广泛应用于边坡稳定性评价、支护设计及评价、地下洞室、拱坝稳定分析、隧道工程、矿山工程等多个领域[3]。

1 FLAC3D动力分析

FLAC3D动力分析中考虑到结构材料的力学性质和大变形的影响，采用等效线性振动分析和非线性振动分析两种方法。等效线性方法是根据试验和工程类比来给定材料的阻尼比和剪切模量进而计算其动力反应，由于建模简单而被广泛用于地震工程学中，模拟地震波在岩土体中传播以及岩土体与结构物间的动力相互作用。非线性动力分析则是考虑材料物理力学性质空间和时间上的非线性，模型中各个单元不同的变形破坏阶段采用不同的阻尼比和剪切模量来计算动力反应。在FLAC3D的动力计算中采取非线性展动分析法，能够真实地模拟地质体的应力－应变关系。

动力分析过程一般分为以下两个步骤:一定地质条件下的静力平衡计算和施加动力荷载后的动力反应分析。在第一步中，确定模型范围、初始条件、材料类型、本构模型以及模型的填筑、开挖、衬砌等，也就是静力作用下的平衡计算;第二步，是在第一步计算的基础上，施加动荷载[4]。

2 工程概况及数值模型

某边坡坡体高为40 m，水平距离35 m，坡顶高程为100 m，其简化模型尺寸如图1所示，上部为岩体，下部为基岩，其物理力学参数如表1所示。

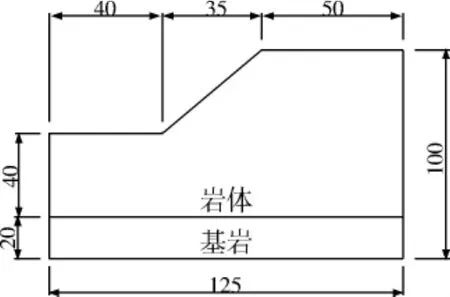
图1 某边坡的简化模型(单位:m)

表1 物理力学参数

该边坡上部采用弹塑性材料，下部采用弹性材料，屈服准则采用Mohr－Coulomb强度准则。由于所选取的边坡计算范围较大，可忽略圣维南效应对边坡稳定性分析的影响。且因边坡的变形和破坏主要发生在坡体的浅部，构造应力在长期的地质过程中已经消失殆尽，因此模型边界不考虑构造应力的作用，只考虑自重应力作用。计算模型所采用的位移边界条件:基底采用刚性边界，同时约束水平方向、竖直方向的位移;左右边界采用水平约束，约束水平方向的位移，只允许竖向沉降;地表边界为自由边界[5]。动力计算是在静力计算的基础上进行的，就是在模型底部施加动力荷载(本文即为地震波)，模型的网格划分及动力边界见图2和图3。模拟时采用的地震加速度时程是由某地震局提供的地震主震数据，为了减少数值模拟计算的时间，只取用幅值较大的前10 s波段作为输入波，图4为其加速度时程曲线。

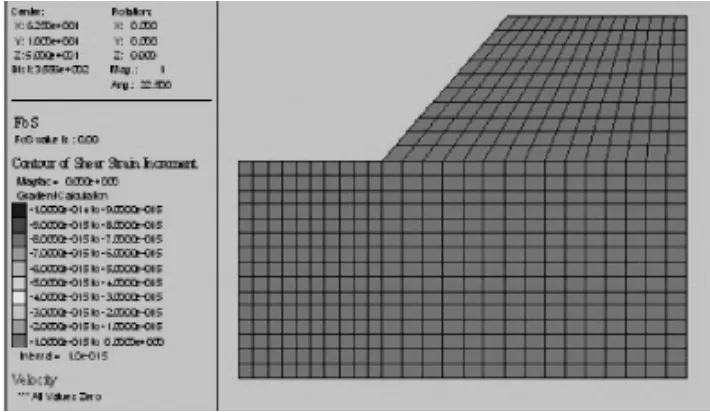
图2 边坡网格划分

图3 模型的动力边界

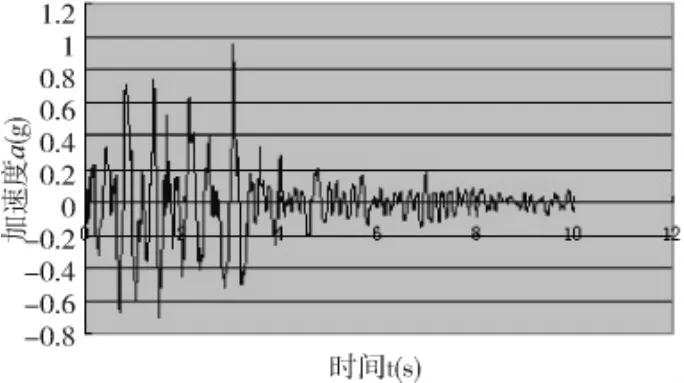
图4 加速度时程曲线

3 模拟结果分析

3.1 天然状态下模拟分析

天然状态下滑坡是否稳定主要取决于最大不平衡力是否收敛，从图5可以看到，最大不平衡力基本上是收敛的，而从图6剪应变分布图可以看出，未出现剪应变集中现象，剪应变主要集中在1×10－15～0，由此可知，天然状态下边坡处于稳定状态。

3.2 地震作用下模拟分析

首先是地震波沿X方向传播的模拟分析，即垂直于坡面方向传播。从图7可以看到，坡体已经出现了明显的剪应变集中带，最大剪应变值达到3.24×10－2，边坡处于失稳状态;再看图8水平位移方向残余位移云图:坡体已出现整体性位移，最大值出现在接近坡脚处，其值达到了－1.31 m，说明在此方向的地震动荷载作用下坡体已经发生大体积滑坡。

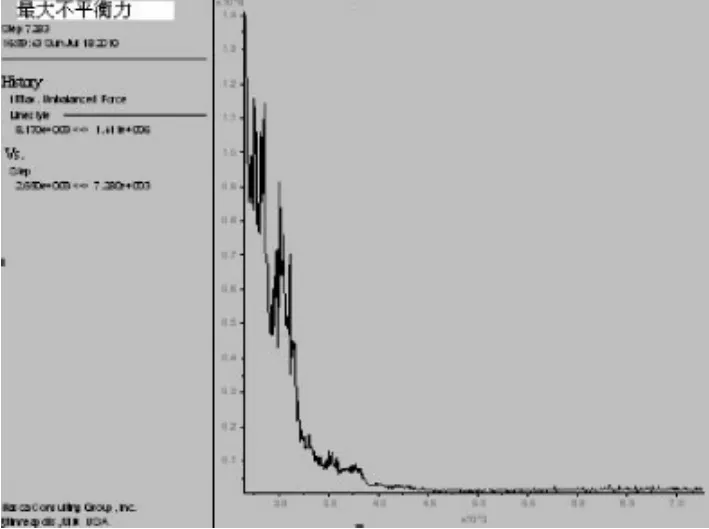
图5 天然状态下最大不平衡力

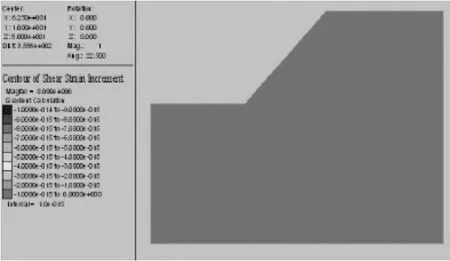
图6 天然状态下剪应变增量分布云图

图7 X方向地震波作用下剪应变增量云图

图8 X方向地震波作用下水平方向残余位移云图

其次是地震波沿Y方向传播的模拟分析，即平行于坡面方向传播。从图9可以看到，坡体出现了明显的剪应变集中带，最大剪应变值达到9.41×10－3，边坡处于失稳状态;再看图10水平位移方向残余位移云图:坡体已出现整体性位移，最大值出现在接近坡脚处，其值达到了－0.47 m，说明在此方向的地震动荷载作用下坡体已经发生滑坡。

图9 Y方向地震波作用下剪应变增量云图

图10 Y方向地震波作用下水平方向残余位移云图

当地震波沿垂直方向传播，即垂直于边坡底部传播。从图11知，坡体已经出现了剪应变集中带，最大剪应变出现在临近坡脚和坡顶处，其值达到1.49×10－2，边坡沿此剪切带将失稳;水平位移方向残余位移云图12:坡体出现局部位移，最大位移值出现在坡体中部，最大值达到－0.59 m，表明在此方向的地震动荷载作用下坡体发生局部滑坡。

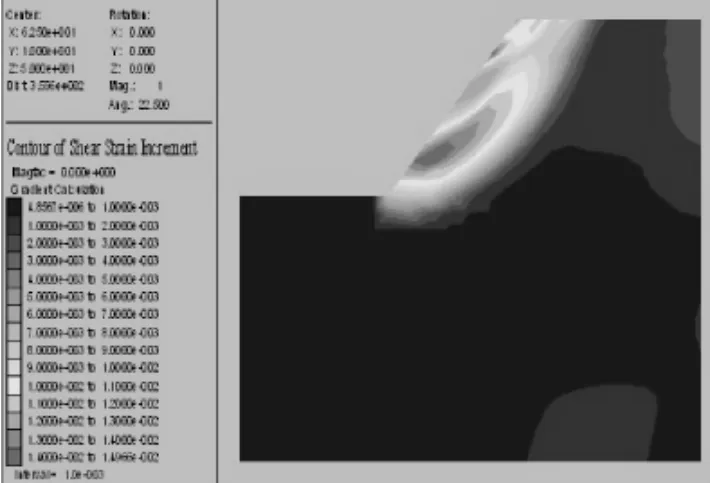
图11 垂直方向地震波作用下剪应变增量云图

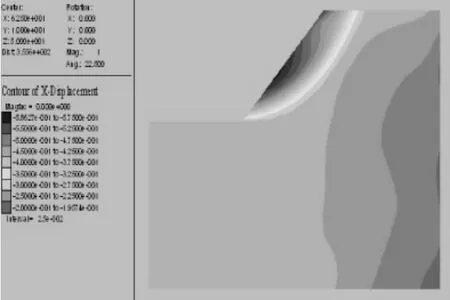
图12 垂直方向地震波作用下水平方向残余位移云图

最后是地震波沿三个方向共同传播的模拟分析，从图13可以看到，坡体已经出现了明显的剪应变集中带，最大剪应变值达到3.64×10－2，边坡处于失稳状态;再看图14水平位移方向残余位移云图:坡体已出现局部位移，最大值出现在接近坡脚和坡顶处，其值达到了－0.91 m，说明在地震动荷载作用下坡体已经发生局部滑坡。

图13 三个方向地震波共同作用下剪应变增量云图

图14 三个方向地震波共同作用下水平方向残余位移云图

4 结束语

结合岩质边坡工程实例，总结了岩质边坡动力稳定性分析的研究成果。目前，虽然岩质边坡动力稳定性分析的研究已经取得了较大进展，但是由于问题本身的复杂性，这些理论和方法还远不能满足工程实际的需要，还需要在理论分析、数值模拟、模型试验和工程经验总结等方面开展更为深入的研究，为工程实际提供理论和技术支持。

[1]赖永标，胡仁喜，黄书珍.ANSYS11.0土木工程有限元分析典型范例[M].北京:电子工业出版社，2007:173－174

[2]王铁行，廖红建.岩土工程数值分析[M].北京:机械工业出版社，2009:86－131

[3]彭文斌.FLAC3D实用教程[M].北京:机械工业出版社，2008:1－3

[4]张友锋，袁海平.FLAC3D在地震边坡稳定性分析中的应用[J].江西理工大学学报，2008，29(5):23－26

[5]周中.土石混合体滑坡的流－固耦合特性及其预测预报研究[D].中南大学，2006