一种在线计算系统阻抗的新方法

裴 健 陈 晨

1.山东电力集团公司 山东 济南 250001；2.东营供电公司 山东 东营 257091

0 引言

变电站母线处的系统戴维南等值电路是系统运行的重要数据，该参数可用于计算系统的短路电流、验证系统的等值网络模型以及进行无功补偿和滤波器的设计等［1-2］。该等值电路参数也可用于计算电压稳定极限［3］以及估计系统的最大负载能力。

估算系统戴维南等值电路的方法可分为两类，干预性方法和非干预性方法：干预性方法通过给系统注入干扰信号，根据电压和电流的响应来估计系统的等值电路参数［4-5］，此类方法的缺点是不能实现实时计算。非干预性方法根据已知的母线电压和支路电流的变化求出系统其余部分的戴维南等值电路参数。文献［6］提出使用约束条件下的最小二乘法来估算系统的短路阻抗参数，但该方法只有在负载为电力电子装置的条件下才能使用。文献［7］提出根据负荷导纳估计系统短路阻抗的方法，但负荷导纳具体数值在大多数情况下难以获得。文献［8］和［9］提出基于同步测量数据求取系统戴维南等值电路参数的方法，但同步数据往往也不易获取。

本文提出一种在线计算系统正序和零序戴维南等值电路参数的非干预性方法。该方法只需变电站馈线的电压电流测量值，独立于系统的模型且不需要同步采样数据。本文还解决了实际工程中可能出现的确定扰动源和负荷波动范围等问题。所提出方法的有效性和精度通过仿真分析和现场测量得以验证。

1 非干预性阻抗估算法

1.1 基本思路

从变电站母线观测到的其余电力系统的等效电路如图1所示。假设系统侧参数Es，Rs和 Xs恒定，据KVL，t1时刻该回路的电压方程为:

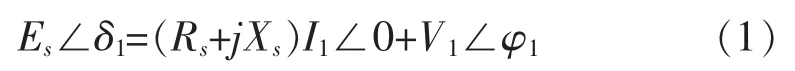
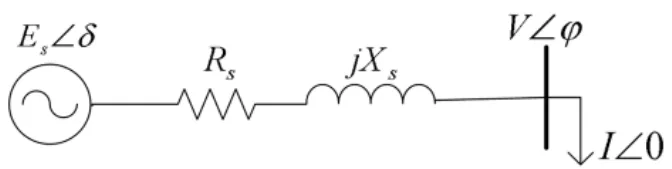
图1 由变电站母线观测到的等效电力系统

方程（1）中有7个变量，其中负荷节点的电压V1和电流I1可测量得到，因此功率因数角φ1也是已知量。可通过以下方法来求解出四个未知量Es，δ1，Rs和Xs［10］，首先建立t2时刻的系统KVL方程：

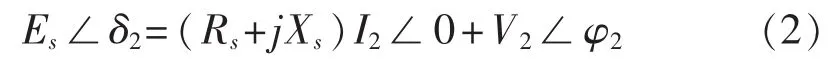
使用同步测量装置，使得t1和t2时刻的测量满足δ1＝δ2，将方程（1）（2）相减，可得:

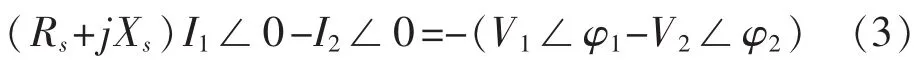
则Rs和Xs可通过公式（4）求出:

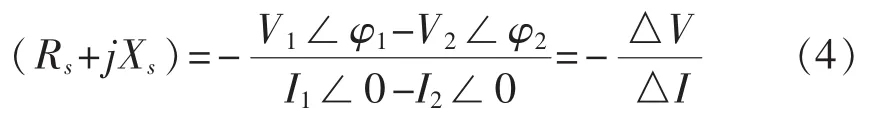
根据计算出的阻抗Rs和Xs以及公式（1）或（2），可求出电压Es。该法非常直接，但公式（4）假设两次测量所取的时间基准相同（即δ1＝δ2），因系统频率的持续变化，此要求在目前的电力系统中无法满足，因此上述方法理论上可行，但实际上无法实现。

1.2 非同步估算法

为克服此缺点，本文提出增加t3时刻的KVL方程，可得

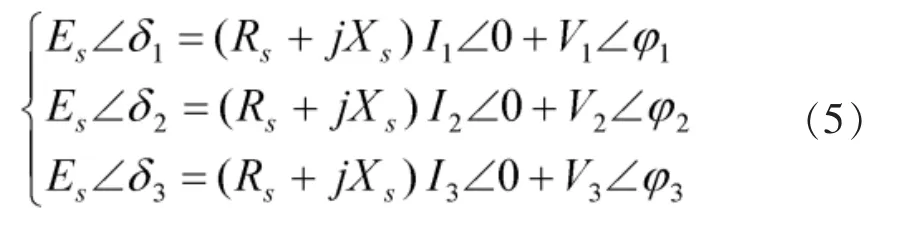
将方程（5）的实部、虚部分开，可得到6个系统方程，而系统共有6个未知变量，可用牛顿拉夫逊法迭代求出结果。

但是该三点估计法对电压和电流测量中的噪声和暂态较为敏感，本节中对三点法进行改进，提出多点估计法。即将三点估计法的求解方程通过增加测量次数扩展到6个以上。首先可将方程（5）改写为：

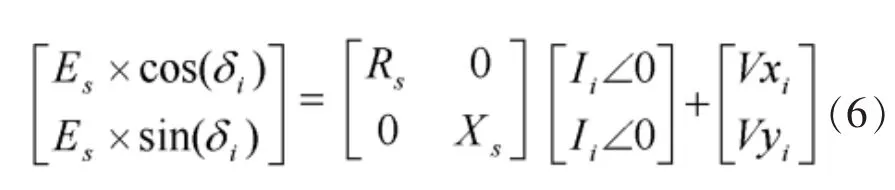
其中，i=1，2，3。假设对n次测量来说，系统参数恒定，通过将（6）扩展到n个测量点可建立（7）：

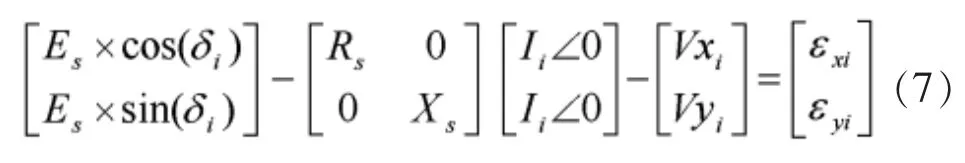
其中i=1，…，n，（n是大于3的任意常数）。 εxi和εyi是估计误差，求解目标是使n次估计值的总误差最小。

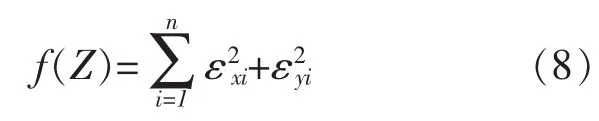
其中，Z＝［Es，Rs，Xs，δi］。 可通过高斯—牛顿迭代法求出使得函数f（Z）取得最小值的向量Z。

为比较三点估计法和多点估计法的性能，特研究两种方法对测量噪声的敏感度。将不同的随机噪声加到电压和电流中，分别使用三点估计法和多点估计法计算系统的正序等效电路参数。将Rs和Xs的精度表达成测量误差的函数，三点估计法和多点估计法的比较结果示于图2中。

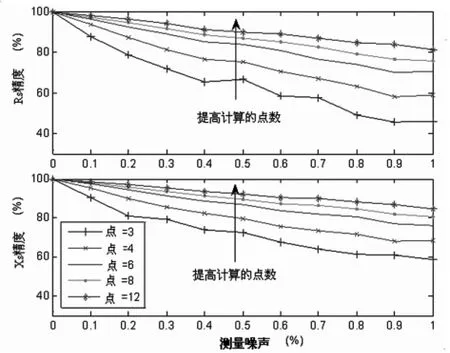
图2 噪声条件下两种方法的精度比较

仿真中负荷随机变化，幅度在10%以内。图2中每一个误差值为运行了300个算例系统的平均估计误差值，计算公式如（9）所示。

2 算法需考虑的二个实际问题

2.1 检测扰动源

为准确估计系统等效电路的参数，多点法需使用三次以上的测量数据，并假设在测量的时间段内，系统侧的参数保持恒定不变。使用本法关键的一点是选择无系统变化的测量点，这实际是一个确实扰动源的问题。本文提出用三点法来确定测量的扰动源，以判断在测量时间段内系统参数是否发生改变。

定义Vi＝Vxi＋jVyi，对公式（5）的等号两侧分别求相量的幅值，得出

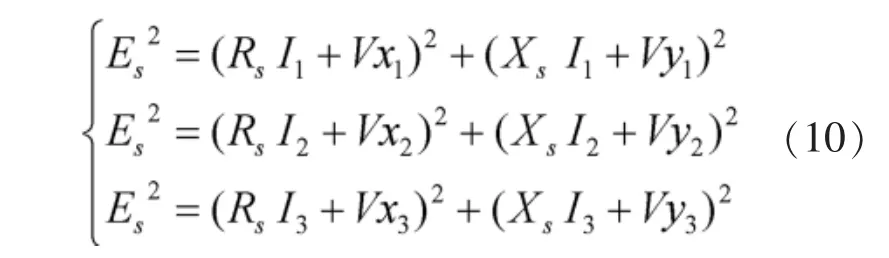
以上3个方程中共含有3个未知数，未知的变量为Es、Rs和Xs。 通过方程（10），可消去Es并将Xs表达成Rs的函数：

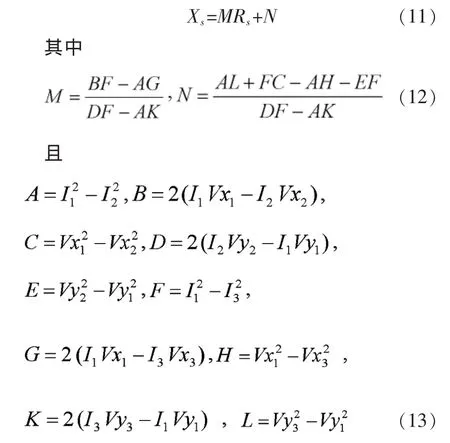
最终，可得出：

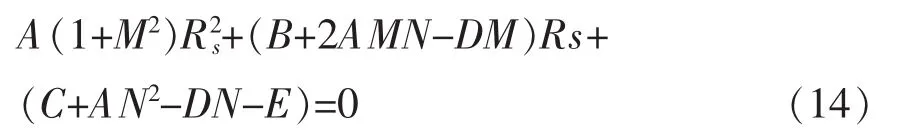
方程（14）为RS的二阶方程，易求解。方程有实数解的条件是△≥0（△=b2－4ac）。△为负值可能在系统参数变化、存在测量噪声以及负荷暂态过程中出现。如果系统侧参数在测量过程中没有变化，则将一定为大于零的数，方程（14）存在1~2个解。

计算出RS之后，可根据公式（6）求出XS和ES，以下的判别标准可用于检查结果的正确性和合理性。

（1）△≥0；

（2） RS， XS和ES应始终为正值；

父母在陪伴阅读过程中，除了要注重与孩子交流沟通之外，还要适当将阅读内容加以拓展，能把这本书中的内容和那本书发生联系，将书中涉及的内容细节和孩子日常生活的场景细节发生联系，真正做到由此及彼，触类旁通。

（3）X/R的比值应在合理的范围以内，具体的数值取决于系统的特性。

三点估计法可用于为多点估计法选取合理的数据。如果方程（14）对于n次测量数据都有三点法的解，即可认为系统参数在测量时间段内没有变化，即可利用更多次的测量数据采用精度更高的多点估计法来计算系统的阻抗参数。

2.2 负荷变化指标

所提出的判别方法基于负荷的变化求出系统的等效短路阻抗参数，负荷波动率定义为式（15）的P和Q的绝对偏差之和。

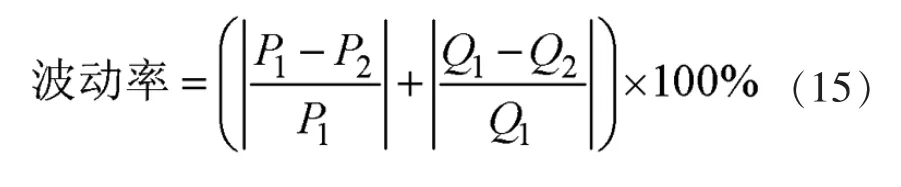
算法的输入数据多于两次测量值，波动指标是测量时间段内的最小加权和。为研究在噪声条件下，测量结果的精度和波动指标之间的关系，进行了灵敏度分析。在不同的负荷水平下，通过将不同的噪声加到所测量的电压和电流中，对算例系统的结果进行了比较，如图3所示。

图3的结果表明，在噪声条件下，通过提高负荷的波动水平，算法的精度可得以提高。工程实际中，负荷电压和电流的微小变化也可计算出结果，因此，所需的负荷波动指标并不需太大。但是电压和电流的幅值应大至可滤除噪声和暂态的影响。本研究中，负荷波动指标接近于0.05%。

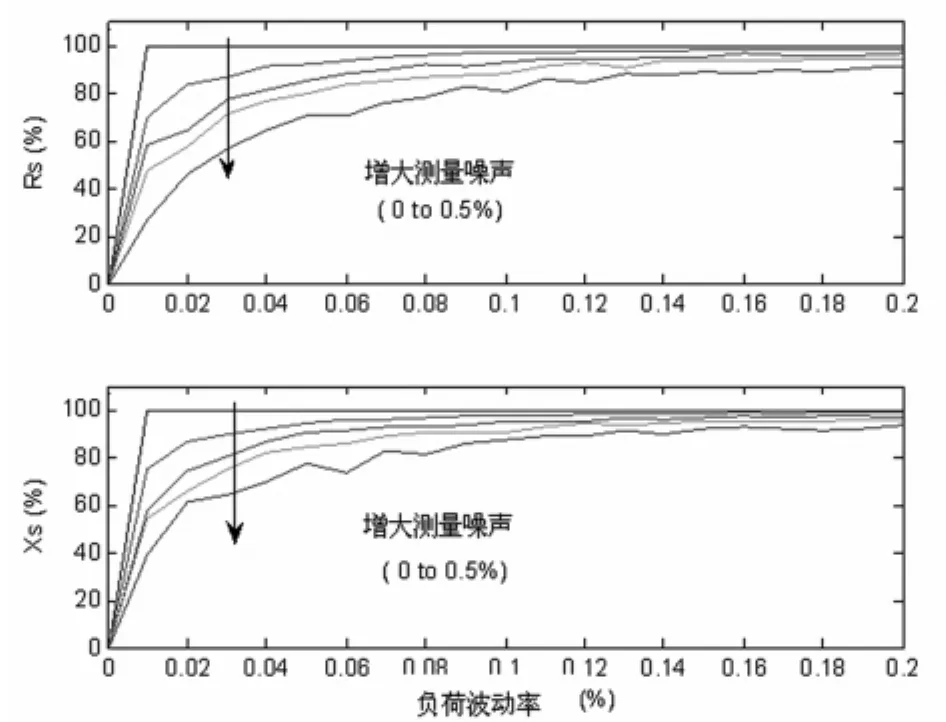
图3 在噪声条件下算法对负荷波动率的精度分析

3 三相系统下的算法

实际电力系统为三相连接，三相电压和电流可转换为正序、负序和零序分量的电压和电流。对于每一相序，都可等效为单相电路，前面针对单相电路提出的算法都可应用于计算正序、负序和零序等值电路的系统参数。三相系统的等效参数估计方法如下：

1）获取3到5秒钟之内的三相电压和电流的测量值；

2）对三相电压和电流的每一个波形的值，利用傅里叶变换转化到频域中；

3）使用对称分量法，计算出正序电压和电流；

4）应用多点估计法计算出正序和零序等值电路的系统短路阻抗参数。

4 现场测试结果

对一10kV实际系统使用所提算法估计其短路阻抗。使用由微机控制的12位的NI-6020E数据采集板记录测量负荷的电压和电流数据，每个周期采样256个点。对馈线采集三相电压和电流，每分钟采集5秒的数据，共采集100分钟。将三相电压和电流利用对称分量法转换出正序、负序和零序的数据。

4.1 正序短路阻抗估算结果

图4画出了馈线的正序电压和电流变化图，利用本文所提算法估算的正序短路阻抗的参数示于图5中。同时，该变电站的短路阻抗参数也采用其它方法计算出。方法1为利用由变电站测量的实际短路数据计算出来的短路阻抗值，方法2为利用实际短路回路计算出的阻抗值（利用PSS/E短路程序）。表1给出了三种方法计算出的系统短路阻抗结果。两种方法结果的微小差异是由于系统中存在的噪声干扰和暂态信号导致的。

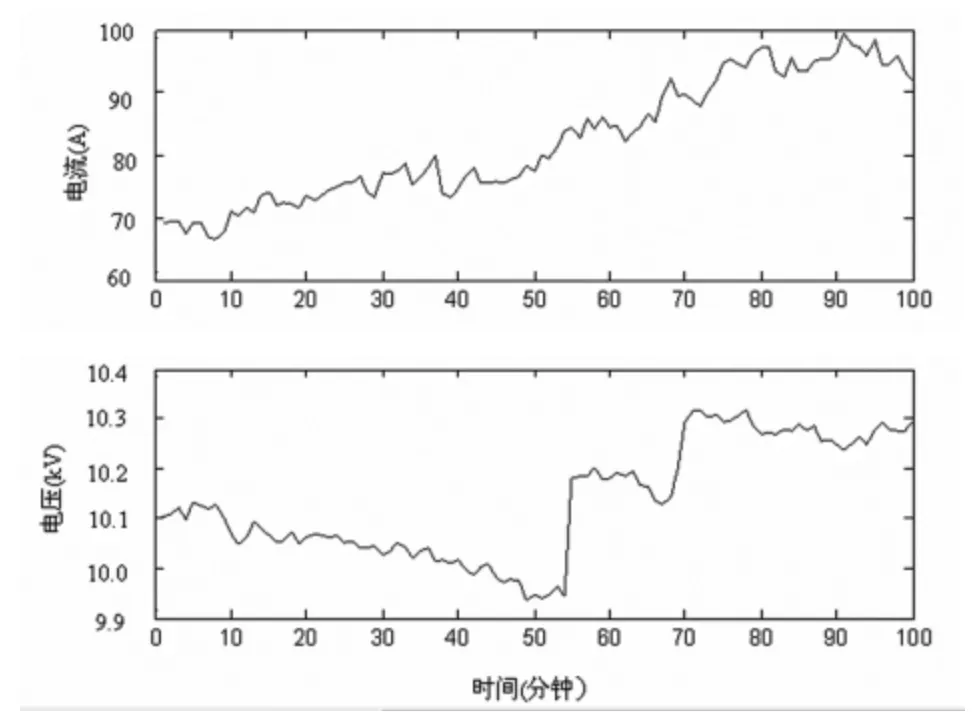
图4 变电站馈线的电压和电流的变化波形图

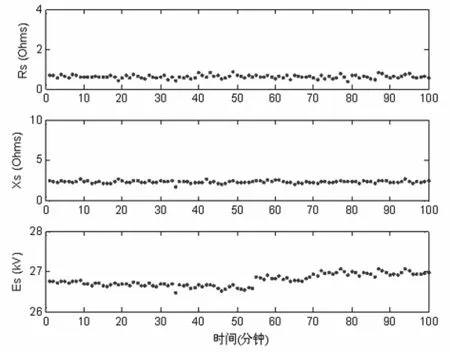
图5 变电站馈线的正序回路阻抗参数

表1 变电站的正序短路阻抗数据

4.2 零序短路阻抗估算结果

图6画出了馈线的零序电压和电流变化图。平均负荷波动率为4.38%。图7给出利用所提算法计算出的馈线的零序阻抗参数，该参数的置信区间为81.3%。测量时间段（1个小时）内馈线的阻抗参数分别为0.341+j2.181Ω。

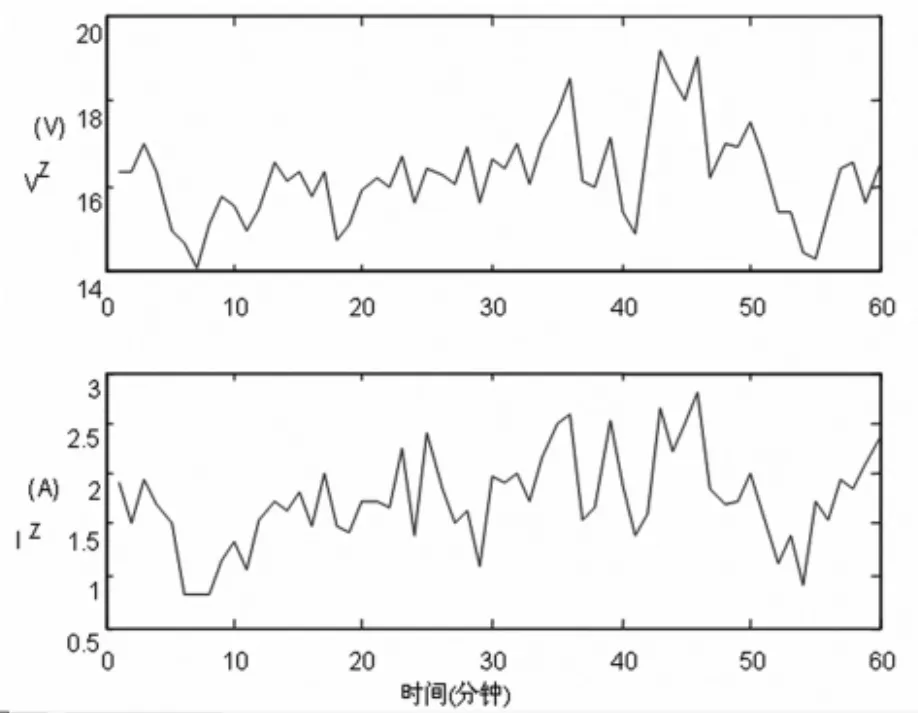
图6 变电站馈线的零序电压和电流的变化图

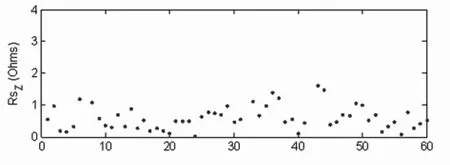
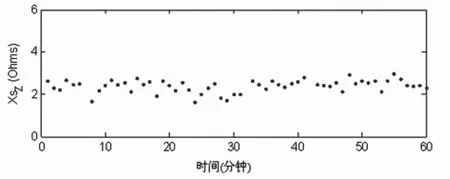
图7 变电站馈线的零序等值电路参数

表2对比了用本文所提方法计算出的阻抗等效参数的平均值和用另两种方法（①使用在变电站记录下的实际故障数据②由PSS/E短路程序得出的数据）计算出的平均值。

表2 变电站的零序阻抗数据

表1和表2的结果说明，可以应用所提出的算法通过零序电压和电流计算系统的零序等值阻抗。这和前面所提出的正序等值电路的计算方法一起可应用于在线估计变电站的故障水平。

5 结论

本文提出了一种在线计算母线处系统正序和零序等值阻抗参数的新方法。该方法可利用现场的数据进行在线估计和预测，并可考虑各种负荷实际运行工况。实际系统的计算结果表明，所提出的算法能够满足系统正序和零序数据的在线监测要求。本文主要结论如下：

1）负荷变化下3～5秒的采样数据即可用来计算出系统的正序和零序等效阻抗参数；

2）每个周期256个采样点的数据采样频率即可满足算法要求；

3）所提的算法不依赖于负荷的种类，可应用于含有各种负荷的工况；

4）不需要同步采样数据；

5）所需的电压和电流数据可从系统中已安装的电压和电流仪表中获得。

［1］王芝茗，王漪，徐敬友等.关键负荷节点集合电网侧戴维南参数估计［J].中国电机工程学报，2002，22（2）：16-20.

［2］罗华伟，吴政球，戴庆华等.电网戴维南等值参数的快速计算［J].中国电机工程学报， 2009，29（1）：35-39.

［3］汤涌，林伟芳，孙华东等.基于戴维南等值跟踪的电压失稳和功角失稳的判别方法［J].中国电机工程学报，2009，29（25）：1-6.

［4］王漪，柳焯.基于戴维南等值的系统参数跟踪估计［J].电网技术， 2009， 24（11）:28-30.

［5］段俊东，郭志忠.一种可在线确定电压稳定运行范围的方法［J].中国电机工程学报， 2006， 26（24）:113-118.

［6］G. Fusco， A. Losi， and M. Russo. Constrained Least Squares Methods for Parameter Tracking of Power System Steady-State Equivalent Circuits ［J]. IEEE Trans. Power Delivery， 2000， 1（15）: 1073-1080.

［7］M. Bahadornejad and G. Ledwich. System Thevenin Impedance Estimation Using Signal Processing on Load Bus Data ［C]. Proceedings of 6th International Conference on Advances in Power System Control， Operation and Management， APSCOM， Hong Kong: 2003.

［8］T. Tayjasanant， Chun Li and W. Xu. A resistance signbased method for voltage sag source detection ［J]， IEEE Trans. Power Delivery， 2005， 20（4）: 2544 - 1551.

［9］K.Vu，and D. Novosel. Voltage instability predictor （VIP）-method and system for performing adaptive control to improve voltage stability in power systems ［P]. U.S. Patent:6，219，591， 1998-05-15.