太阳能光伏电池工程近似模型与实测检验

王砥凡 张 桦 刘勇超

1.临沂供电公司 山东 临沂 276000；2.重庆电力公司 重庆 400014；3.山东电力科学研究院 山东 济南 250002

0 引言

使用化石燃料给人类带来的能源危机、环境污染、生态破坏等问题促使人们将更多的注意力转移到清洁、可再生能源上来，太阳能作为一种分布广泛、绿色清洁的能源，成为继化石燃料之后国际上公认的理想替代能源。随着光伏电站数量的增多及规模的扩大，光伏电站运行方式、并网方式及对电网的影响的研究需要在现有基础上进一步深入，而研究必须以正确实用的光伏电池模型为基础。现有的光伏电池理论模型在原理上正确，但是一些参数不好测得，厂商也无法提供；工程模型更加贴近工程实际，可以结合实测曲线计算得出，但是又不够精确，在环境条件变化的情况下有时会产生很大的误差，所以，对光伏电池建模的研究仍然是必要的。

1 光伏电池理论模型及仿真分析

光伏电池的基本结构是能够将光能转换为电能的PN结，因此其模型符合二极管的特性，图1显示了光伏电池理论模型等效电路［3］，根据等效电路可以写出光伏电流输出特性的非线性方程组如式（1）~（3）。

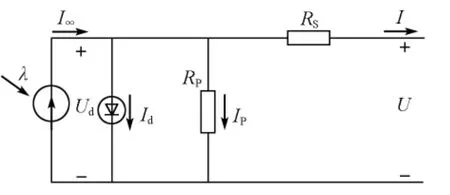
图1 光伏电池精确的等效电路模型

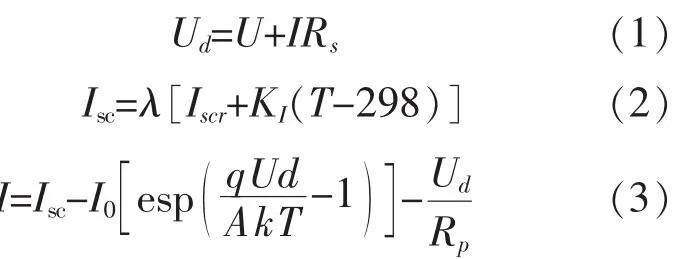
式中各变量含义如下：A为二极管的理想因子；k为玻尔兹曼常数，k＝1.38×10－23J/K；T为开氏温度K；q为电荷电量，q＝1.6×10－19C；λ 为光照强度，单位kW/m2；Iscr为标准测试条件光照强度1kW/m2及环境温度为298K时所测得的光生短路电流；KI为光生电流随温度变化系数，典型值为0.0017。

此模型可精确地描述光伏电池的输出特性，但是在模型中需要知道6个参数，即二极管理想因子A、标准测试条件下光生短路电流Iscr、光生电流随温度变化系数KI、光电池PN结反向饱和电流（暗电流）I0、串联电阻Rs、并联电阻Rp，这些参数厂商不会全部给出，需要根据实测曲线拟合，若直接采用6个实测点带入，采用迭代法解6元非线性方程，则迭代不一定能够保证收敛，并且方程的解对初值敏感，难以获得真实准确的模型参数。尤其是在最大功率点附近，如果带入方程的数据点出现一点误差，解出的参数可能有数量级上的差别。根据（1）式和（3）式使用MatLab仿真光伏电池的输出曲线如下图2，如果在求解参数的时候带入了有些许误差的数据，并联电阻Rp可能出现两个数量级的差异。

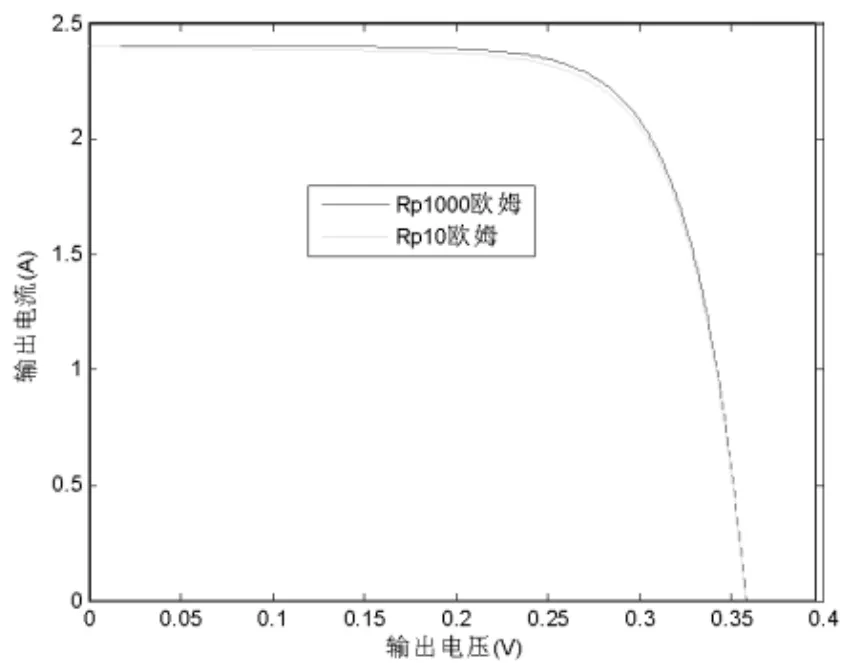
图2 单个光伏电池单元输出特性对比

这种在单个电池上的参数差异如果应用于全电站建模，就会被放大，导致模型出现较大的误差，根据上述两个不同的并联电阻值，建立20个电池串联的模型，则两个模型的差异很大（如下图3）。因此如果想得到电池组的准确模型，对单个太阳能电池模型的参数就要有很高的精度要求，而在测量中这是不好实现的。

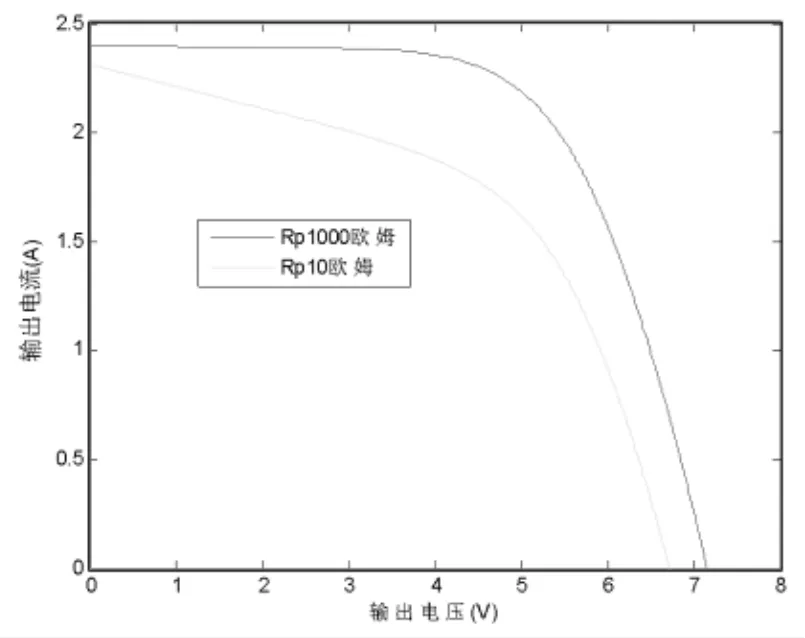
图3 光伏电池阵列输出特性对比

2 光伏电池工程模型及仿真分析

根据光伏电池的精确模型进行简化，忽略掉较小的串联电阻Rs及较大的并联电阻Rp的影响，可以得到工程简化模型如下式：

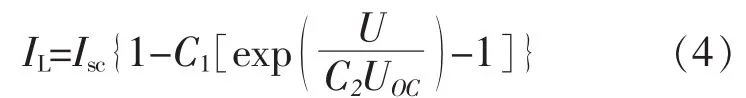
其中UOC、Isc分别为光伏电池的开路电压、短路电流。如果再有一个测量点，如最大功率点的输出数据Um、Im，就可以计算得到两个系数C1、C2：

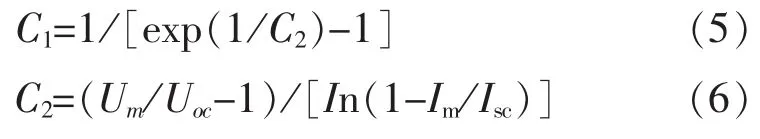
但是此参数是在标准测试条件光照强度（1kW/m2）及环境温度为298K时的数据，如果光照强度或环境温度发生变化，则还需要对输出特性进行修正：

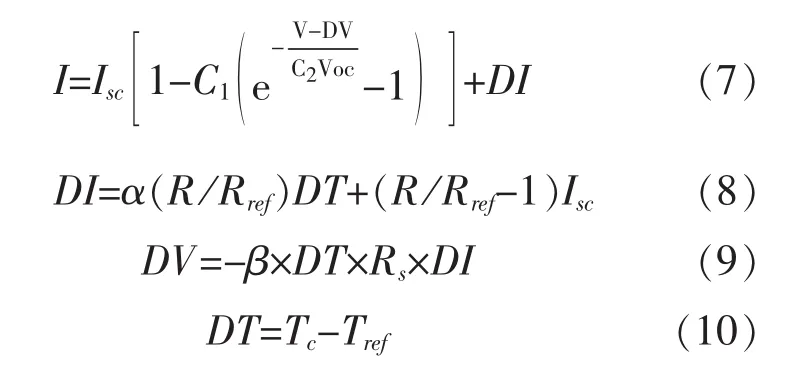
此修正仍然需要引入参考日照下的电流变化温度系数α（Amps／℃）、参考日照下的电压变化温度系数β（V／℃）及光伏阵列的串联电阻Rs，如果不对结果进行修正，则仿真与实测值会有较大误差。

在标准光照强度及实验温度下，光伏电池的理论模型和工程模型仿真得到的结果是相同的，图4为两个模型的输出曲线。

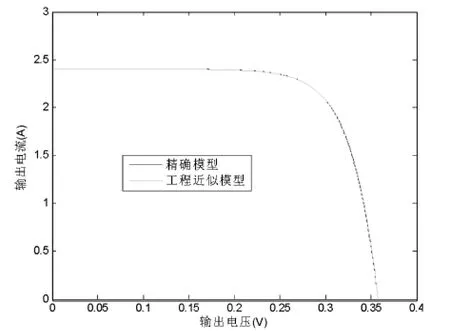
图4 标准条件下两种模型仿真结果

但是在温度及光照强度变化之后，在标准条件下测定的开路电压、短路电流均与当前条件下的相应电气量不符，因此工程模型会出现较大的误差，图5是在环境温度300K、光照强度0.9倍的情况下得到的光伏电池输出曲线。采用理论模型得到的温度及光照强度变化后的曲线是真实的，而工程近似模型由于参数未能根据实际情况的变化做出相应调整，给出的曲线误差较大。

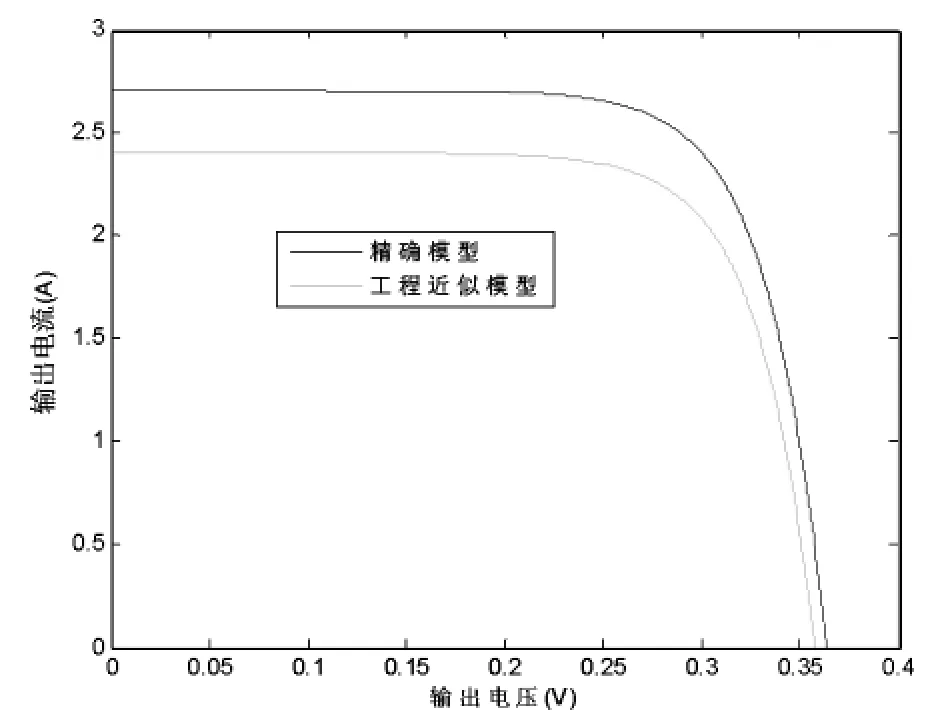
图5 非标准条件下两种模型仿真结果

此时需要根据式（7）~（10）对工程近似模型作出修正，仿真中使用电流变化温度系数α=0.0017，电压变化温度系数β=0.0005，修正之后的工程模型与精确模型已经非常近似（图6）。

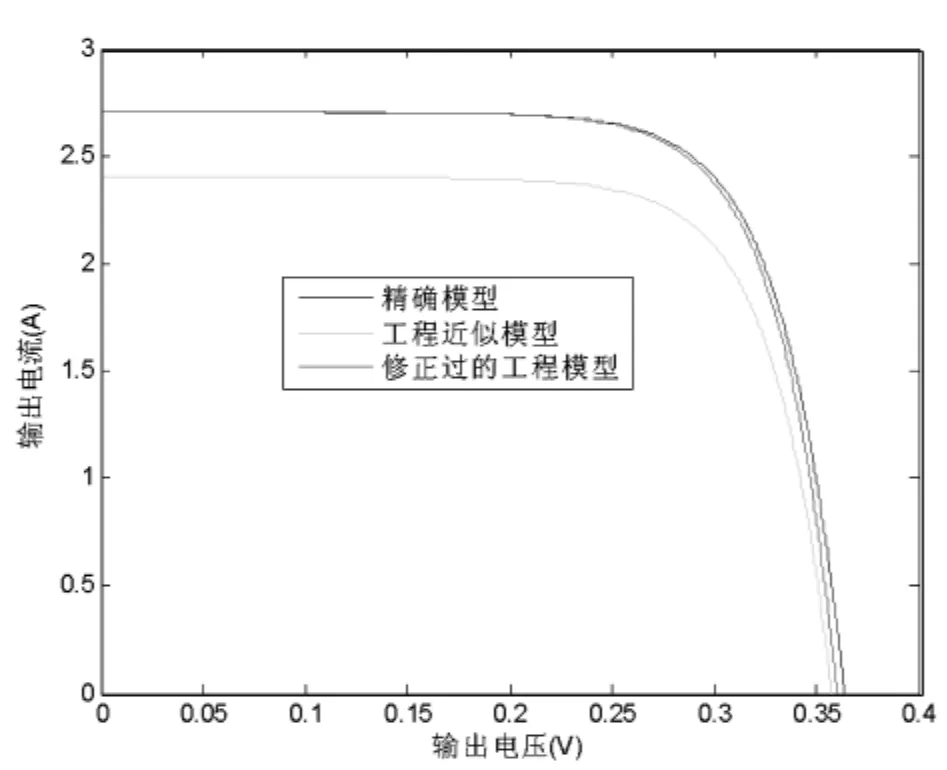
图6 修正之后的工程模型仿真结果

3 光伏电池实测模型

国家电网技术学院新能源实验室对太阳能光伏电池板进行了实测检验，光照强度700W/m2，光伏组件温度51.2℃，测量电池板参数如下表1：

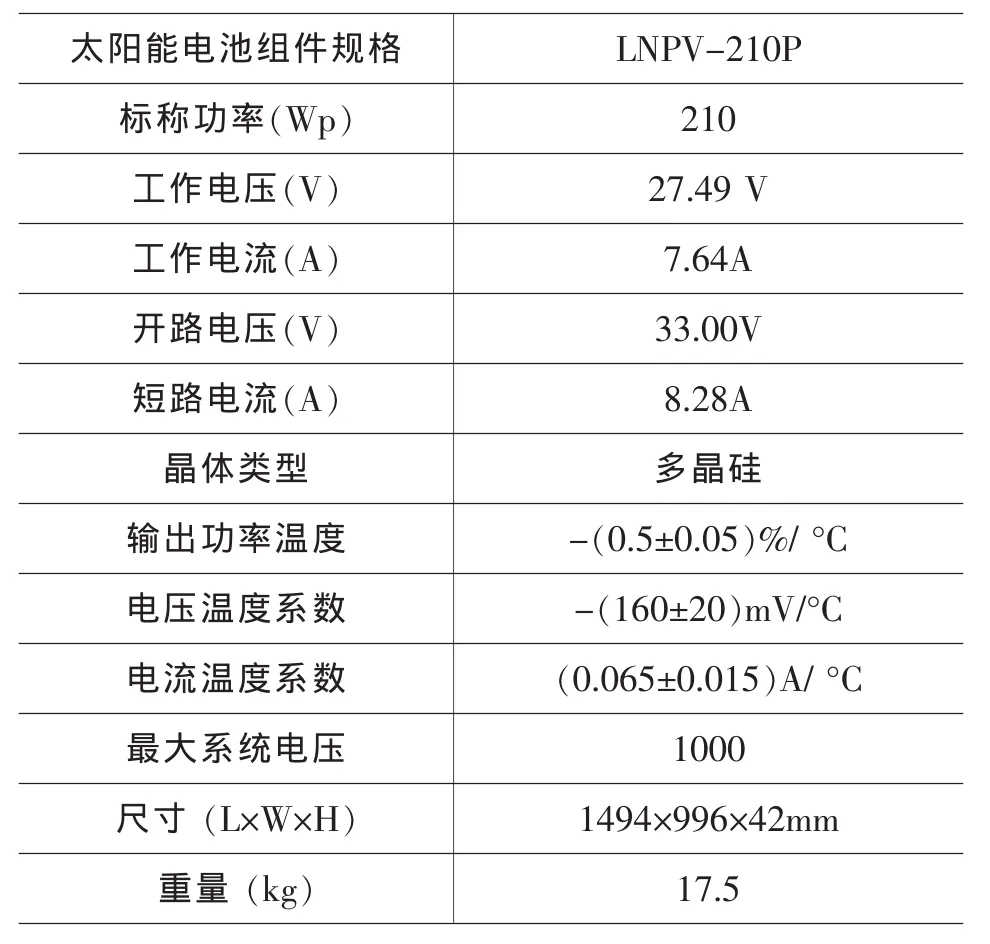
表1 太阳能电池板实测参数表

根据实测参数，α＝0.065，β＝0.160，工程近似模型、修正结果及实测结果三者比较如图7：

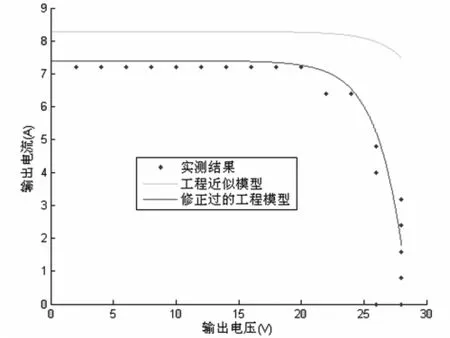
图7 仿真结果与实测结果比较

比较发现，未修正的工程模型完全不能反映非标准条件下光伏电池的特性，而修正过的工程模型与实测结果吻合的很好。

4 结论

文章针对目前太阳能电池板的精确模型和工程近似模型做了理论及仿真分析，指出了太阳能电池板的精确模型参数不易获得的缺点，同时仿真验证了工程近似模型在标准条件下的可行性。在非标准条件下，可以借助修正算法对工程近似模型进行修正，得到近似度较高的结果。

［1］赵争鸣.太阳能光伏发电及其应用 [M].北京：科学出版社,2005.

［1］Zhengming Zhao. The Solar Energy Photo -voltage Technology［M］. Bejing:Scince Press， 2005.

［2］Masters G M. Renewable and efficient electric power systems［M］. Hoboken， NJ: Wiley， 2004.

［3］IEEE STD 929 -2000. IEEE Recommended Practice for Utility Interface of Photovoltaic （PV） Systems ［S］. New York: The Institute of Electrical and Electronics Engineers， 2002.

［4］赵晶，赵争鸣，周得佳.太阳能光伏发电技术现状及其发展［J］.电气应用，2007，26（10）：6-11.

［5］于静，车俊铁，张吉月.太阳能发电技术综述［J］.世界科技研究与发展，2008，30（1）：56-59.

［6］周德佳，赵争鸣，袁立强，冯博.300kW光伏并网系统优化控制与稳定性分析［J］.电工技术学报，2008，23 （11）：116-122.

［7］茆美琴，余世杰等.带有MPPT功能的光伏阵列Matlab通用仿真模型［J］.系统仿真学报，2005，17（5）：1248-1251.

［8］王长江.基于 MATLAB 的光伏电池通用数学模型［J］.电力科学与工程，2009，（4）：11-14.

［9］李晶，许洪华，赵海翔，彭燕昌.并网光伏电站动态建模及仿真分析［J］.电力系统自动化，2008，32（24）：83-87.

［10］周德佳，赵争鸣，吴理博，袁立强，孙晓瑛.基于仿真模型的太阳能光伏电池阵列特性的分析［J］.清华大学学报（自然科学版），2007，47（7）：1009-1112，1117.