基于MATLAB的光伏MPPT仿真研究

张红光，宋吉江，翟义成，陈 洁，刘圆圆

（山东理工大学电子与电气工程学院，山东淄博255091）

光伏阵列最大功率跟踪（maximum power point tracking，MPPT）控制是光伏系统的重要组成部分，其目的是使光伏阵列始终输出最大的功率．只有功率最大输出才能够充分地利用太阳能，减少损耗．目前太阳能电池直接获得的能量不稳定，即电压电流随着光照和温度是可变的．为了解决这一问题，加入了DC／DC功率转换模块，使得输出的电压基本稳定，能量得到最大利用．本文采用优化的MPPT算法，并通过模拟仿真的方式来验证该算法是否可行．

1 光伏电池特性分析

1．1 光伏电池数学模型

根据图1所示的光伏电池的等效电路，可以得到光伏电池的输出特性表达式［1－2]：

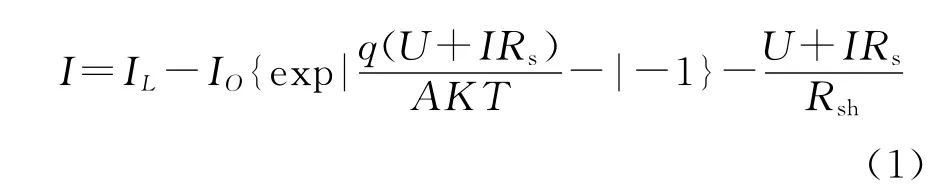
式中：IO表示二极管反向饱和电流；q表示电子荷；K表示波尔兹曼常数；T表示绝对温度；A表示二极管因子；U表示光伏电池输出电压；I表示光伏电池输出电流；Rs表示电池内阻；Rsh表示二极管反向饱和漏电流．

式（1）中的各项参数与电池的温度和光照有关，而且也很难确定，且在工程应用中不常使用．通常情况下，依据电池的特性参数简化物理模型，得到工程数学模型［3]

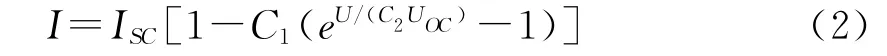
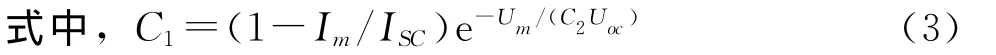
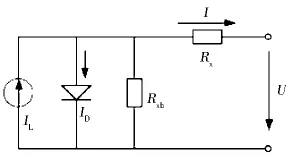
图1 光伏电池等效电路图

根据（2）—（4）式，利用MATLAB／simulink模块建立光伏电池的仿真模型．如图2所示．

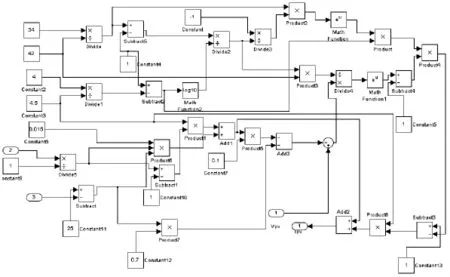
图2 光伏电池模型

1．2 输出特性分析

不同温度下的输出特性曲线如图3和图4所示

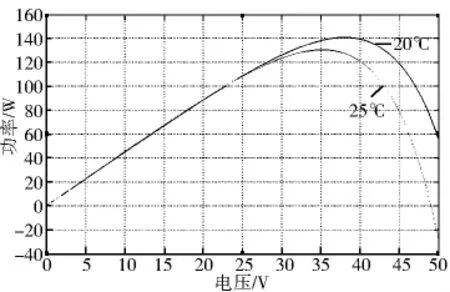
图3 不同温度下的P－V曲线

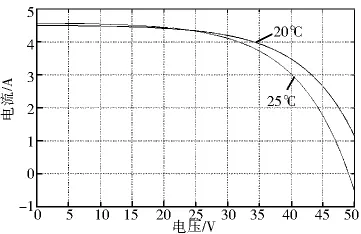
图4 不同温度下的I－V曲线

随温度变化而改变从仿真曲线可以看出，光强一定时，光伏电池最大功率；输出电流基本上不变；光伏电池功率输出呈非线性，随着输出电压的增大，功率有一个最大值，有必要进行最大功率点的跟踪．

2 MPPT仿真算法分析

光伏整列正常工作时，输出电压以微小值不断波动靠近最大功率点时的电压值，在输出电压变化的同时，检测输出功率变化的方向，从而确定下一次变化方向，确定下一次输出电压参考值的大小．算法流程图如图5所示．

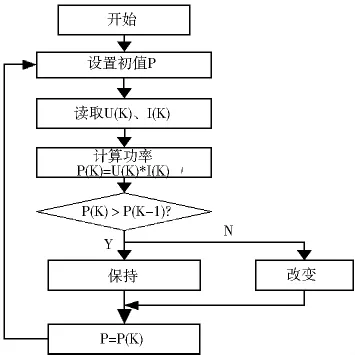
图5 控制算法流程图

Matlab／Simulink中搭建仿真模型如图6所示．扰动步长大小的确定尤为重要，扰动步长太小，到达稳态后精度较好，但跟踪时间长且系统动态性能较差；扰动步长太大，跟踪时间虽缩短，但到达稳态后精度会变差．该算法通过加入滞环来实现扰动，通过改变步长值，并对光伏系统模型进行仿真，最终得出步长取0．01仿真效果最为理想［4]．光伏系统输出功率曲线如图7所示．

3 仿真实验

根据以上算法建立的模型，参考电池参数为开路电压42V，短路电流4．5A，峰值电压34V，峰值电流4A［5]．在光伏电池后加入功率转换电流DC／DC模块，采集电压电流后控制pwm模块来实现最大功率点跟踪．光照和温度由阶跃信号提供，光照由1kW下降到0．8kW后系统能够快速响应，并稳定在一定值．如图7所示，分别是电压、电流、功率跟踪曲线．

4 结束语

本文采用MATLAB中的simulink模块对光伏电池及MPPT控制模块进行了仿真验证，证明具有可行性．虽然光伏电池模型没有使用S函数编写，精确性有所下降，但是这样的模型方便使用，同时还可以作进一步改进．

图7 功率跟踪曲线

［1] 王立乔，孙孝峰．分布式发电系统中的光伏发电技术［M] ．北京：机械工业出版社，2010：25－35．

［2] 王长贵，王斯成．太阳能光伏发电实用技术［M] ．第二版．北京：北京化学工业出版社，2009：33－46．

［3] 高厚磊，田佳，杜强，等．能源开发新技术－－分布式发电［J] ．山东大学学报：工学版，2009，39（5）：107－108．

［4] 周德佳，赵争鸣，吴理博，等．基于仿真模型的太阳能光伏电池阵列特性的分析［J] ．清华大学学报：自然科学版，2007，47（7）：1 109－1 112．

［5] 唐渝，赵莉华．光伏发电的最大功率点跟踪控制［J] ．电源世界，2010（6）：48－51．