基于LCC的超声波电动机驱动电路分析

傅 平

(闽江学院，福建福州350108)

0引 言

超声波电动机［1-3］具有低速大力矩的特点，已在许多领域得到了应用，如镜头自动对焦、精密XY平台等。超声波电动机的二相驱动输入在机械上相互耦合，因此转子二相能量转换过程中不可能完全相等，转子的二相等效负载也不可能完全相等，随工作情况的不同，其等效电路也会发生变化。

本文基于LCC的电路来驱动超声波电动机。此电路工作在其几何谐振频率，超声波电动机二相驱动输入电压基本不受电机品质因数变化的影响。与串联或并联LC谐振驱动电路相比，它只增加了二个电容。

1超声波电动机驱动电路

基于LCC的超声波电动机驱动电路示意图如图1所示。整个电路由半桥电路和二相LCC驱动电路组成。

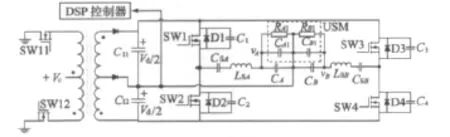
图1 二相半桥式LCC驱动电路

本文采用的超声波电动机的工作频率为49～52 kHz。实际开关元件的工作频率为50～55 kHz，略高于其机械谐振频率。开关元件的频率由DSP控制器加以控制，DSP控制系统的框图如图2所示。其中PWM1～PWM4分别为驱动开关元件SW1～SW4的信号，PWM5～PWM6为驱动开关元件SW11～SW12的信号。

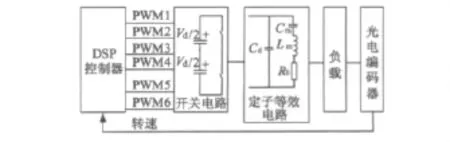
图2 DSP控制系统框图

2 LCC驱动电路分析

图3(a)为单相(如A相)LCC驱动电路的等效电路图，其中SW1和SW2为MOSFET场效应管，CSA为串联谐振电容，CPA为CA与CA1的并联等效电容，CSA=CA1+CA。

在以下分析之前，对有关器件作以下假设:①所有场效应管和二极管为理想器件;②电感、电容和变压器为理想元件;③变换器采用变频控制策略，同一桥臂开关管180°互补导通;④开关频率高于谐振频率，变换器工作在谐振电感电流连续模式。图3给出了变换器稳态工作时的等效电路图，各开关模态的工作情况描述如下:

(1) 开关模态Ⅰ(即［t0，t1］阶段)，如图 3(b)所示。设初始时刻为t0，在t0时刻之前，SW1关断。C1对LSA、CSA放电。由于电感电流处于连续状态，C2开始充电。当Vc1为零时，D1导通。由于C2的存在，使Vc2的变化速度变慢，减小了SW2的关断损耗。

(2) 开关模态Ⅱ(即［t1，t2］阶段)，如图 3(c)所示。在t1时刻对SW1施加驱动信号。流过D1的电流减小到零。D1自然截止，为零电流关断。SW1零电压导通。在此过程中，能量从电源流向谐振电路。

(3) 开关模态Ⅲ(即［t2，t3］阶段)，如图 3(d)所示。在t2时刻之前SW1的驱动信号使其截止。C2对LSA、CSA放电。又由于电感电流的连续性，当Vc2为零时，D2导通。与开关模态Ⅰ类似，C1使SW1关断损耗降低。

(4) 开关模态Ⅳ(即［t3，t4］阶段)，如图 3(e)所示。在t3时刻之前施加SW2的驱动信号。当SW2导通后，D2的电流减小到零，D2自然截止，SW2零电压导通。在这个阶段，能量存在于谐振电路中，向负载传递。输出电压vA由谐振电路产生。另外由于谐振电路的选频性，vA为输入方波信号的基波。

图3 各开关状态下的等效电路

3仿真分析

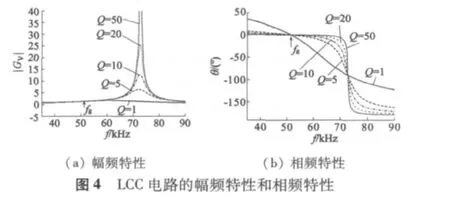
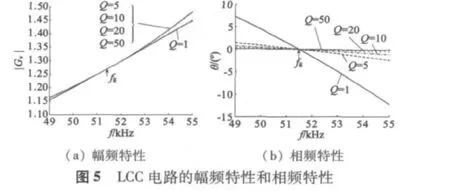
本文采用的电机为Φ30 mm行波型超声波电动机，取 LSA=LSB=1．2 mH，CSA=CSB=CPA=CPB=CA+CA1=8 nF，其中CA1和CB1为电机静止时的测量换算值。由电路分析计算可以得到其谐振频率fs1=72．9 kHz，几何频率 fg=51．5 kHz。当 Q 取不同值且系统的开关频率在［35，90］kHz时，图4(a)、图4(b)分别表示计算得到的LCC电路幅频特性和相频特性。由图中可见，在整个频率变化范围内，系统的幅频特性和相频特性变化较大;当系统的开关频率在几何频率fg附近时，即使品质因数变化较大，电路的幅频特性和相频特性变化也不大。当工作频率设计为50～52．8 kHz之间变化，图4中的一部分经放大后在图5中显示。在此变化范围内，图5(a)的幅频特性变化范围小于3．5%。另一方面，超声波电动机工作时其驱动系统的品质因数一般都大于10，由图5(b)可以得到系统的相位变化小于2°。因此二相输出电压vA、vB基本相等，超声波电动机运行时可以获得较好的动态性能。

当电机转速为250 r/min时，经测试其等效电容 CA1、CB1变为2．7 nF，由此可以得到图 6(a)、图 6(b)的幅频特性和相频特性。从图中可见，当品质因数Q变化范围较大时，电机在几何频率附近的幅频特性和相频特性变化小于4%。因此，当超声波电动机工作导致等效电路参数发生变化时，电机也可以保持较好的动态性能。

图6 参数变化时LCC电路的幅频特性和相频特性

4实验结果分析

实验使用的电机为Φ30 mm行波型超声波电动机，半桥电路的输入电压Vd=230 V(DC)，LSA=LSB=1．2 mH。

图7为LCC驱动电路实物图。图8～图10中vA、vB为电机二相驱动电压，UDS为开关元件漏极与源极的电压差(即半桥电路的输入电压)。图8是LCC电路开关频率fs设为48 kHz时驱动电路的输出波形，图8(a)、图8(c)中驱动电压 vA落后 vB90°，此时转速为零，驱动电压峰峰值VPP为294 V;图8(b)、图8(d)中驱动电压vA超前vB90°，此时转速为零，驱动电压峰峰值VPP为292 V。从图中可以看出，其二相驱动电压基本一致，而且由图8(a)可见vA与半桥电路输入电压的相位差为0°，图8(b)的情形与此类似。

图9是开关频率fg设为50 kHz时LCC驱动电路的输出波形，与图8类似，图9(a)、图9(c)中驱动电压vA落后vB90°，此时转速为180 r/min，驱动电压峰峰值VPP为296 V;图9(b)、图9(d)中驱动电压vA超前vB90°，此时转速为183 r/min，驱动电压峰峰值VPP为298 V，此时vA与半桥电路输入电压的相位差约为1°。

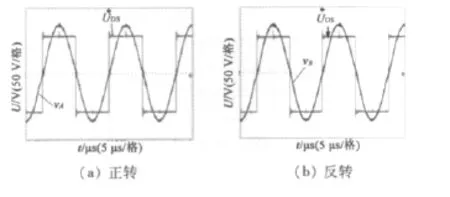
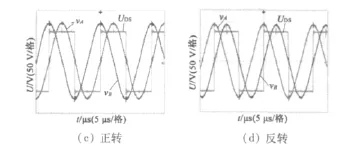
图9 fs=50 kHz驱动电路输出波形

图10为fs取51．5 kHz且电机带0．02 N·m负载时驱动电路的输出波形。图10(a)、图10(c)中驱动电压vA落后vB90°，此时转速为100 r/min，驱动电压峰峰值VPP为296 V。图10(b)、图10(d)中驱动电压vA超前vB90°，此时转速为98 r/min，驱动电压峰峰值VPP为294 V，vA与半桥电路输入电压的相位差为0°。由图8～图10可见，其二相驱动电压vA、vB基本相等且在仿真的幅度特性误差范围之内，即驱动电压基本不受驱动频率的影响，只由半桥电路的输入电压Vd控制，交流增益相位角与理论计算基本一致。

图10 fs=51．5 kHz驱动电路输出波形

在上述驱动频率下经测算得到的品质因数如表1所示。

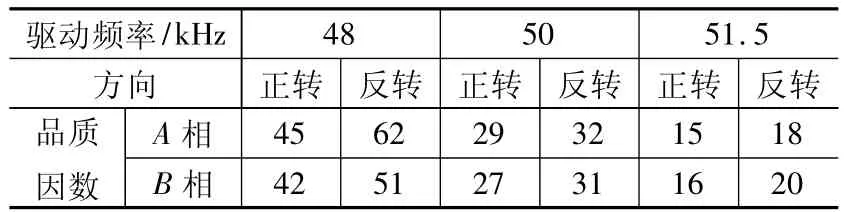
表1 不同频率时的品质因数

5结 语

本文从基于LCC的超声波电动机驱动电路出发，分析了LCC驱动电路开关模态的工作情况，然后通过仿真和实验加以验证，其结果与理论分析一致:在LCC驱动电路的几何频率附近区间内，驱动电路输出电压的幅度基本不受电路品质因数变化的影响。实验结果也验证了此电路的有效性。

基于LCC的超声波电动机驱动电路为超声波电动机驱动提供了一种有效的思路，为电机控制性能的提升打下了基础。

［1］ 胡敏强，金龙．超声波电机原理与设计［M］．北京:科学出版社，2005．

［2］ Hagood N W，Mcfarland A J．Modeling of a piezoelectric rotary ultrasonic motor［J］．IEEE Trans．Ultrasonics，Ferroelectrics and Frequency Control，1995，42(2):219-224．

［3］ Mass J，Grotstollen H．Dynamic analysis of inverter fed ultrasonic motors［C］//Proceedings of IEEE-PESC．1996:1780-1786．

［4］ Furuya S，Maruhashi T，Izuno Y，et al．Load adaptive frequency tracking control implementation of two phase resonant inverter for ultrasonic motor［J］．IEEE Trans．Power Electron．，1992，7(3):542-550．

［5］ Izuno Y，Takeda R．New fuzzy reasoning-based high-performance speed position servo control schemes incorporating ultrasonic motor［J］．IEEE Trans．Ind．Appl．，1992，28(3):613-618．

［6］ Senjyu T，Uezato K．Adjustable speed control of ultrasonic motors by adaptive control［C］//Proceedings of IEEE-PESC．1994:1237-1242．

［7］ Faa-Jeng Lin，Rong-Jong Wai，Mu-Ping Chen．Wavelet neural network control for linear ultrasonic motor drive via adaptive sliding-mode technique［J］．IEEE Trans．Ultrasonics，Ferroelectrics and Frequency Control，2003，50(6):686-698．

［8］ Izuno Y，Nakaoka M．High performance and high precision ultrasonic motor-actuated positioning servo drive system using improved fuzzy-reasoning controller［C］//Proceedings of IEEE-PESC．1994:1269-1274．

［9］ Lin F J．Fuzzy adaptive model-following position control for ultrasonic motor［J］．IEEE Trans．Power Electronics，1997，12(2):261-268．

［10］ 顾菊平，胡敏强．超声波电机谐振升压式驱动技术研究［J］．中国电机工程学报，2002，22(8):49-52．

［11］ 李华峰，赵淳生．基于LC谐振的超声电机驱动器的研究［J］．中国电机工程学报，2005，25(23):145-147．

［12］ Lin F J，Kuo L C．Driving circuit for ultrasonic motor servo drive with variable-structure adaptive model-following control［J］．IEE Proc．，Electr．Power Appl．，1997，144(3):199-206．

［13］ Kazimierczuk M K，Abdulkarim A．Current source parallel resonant DC/DC converter［J］．IEEE Trans．Industrial Electronics，1995，42(2):199-208．

［14］ Batarseh I，Lee C Q．High-frequency high-order parallel resonant converter［J］．IEEE Trans．Industrial Electronics，1989，34(4):485-498．