基于自适应细分技术的步进电动机加减速控制
张晓旭,刘景林,舒宗燕
(西北工业大学,陕西西安710072)
0引 言
本系统研究背景是基于某二维运动机构的稳定控制。运动机构采用步进电动机驱动X(水平)方向和Y(垂直)方向的负载运行,为了实现二维运动机构的快速跟踪和扫描,这就要求步进电动机频繁地工作在加减速状态,或者在某一恒速下维持跟随运行,因此,控制系统既要保证步进电动机转速的平滑切换,又要使电机在各个速度范围都能稳定运行,这就对电机的加减速控制有着较高的要求。
然而,传统上步进电动机加减速是在固定细分状态下进行的,即细分数在加减速前后固定不变。这种方式不利于系统在宽速范围下的稳定运行,存在局限性。若步进电动机在高细分状态进行加减速,则低速性能优异,转矩脉动噪声也得到较好的抑制,但却导致高转速上不去,调速范围窄;若电机工作在低细分状态下,解决了高转速问题,但在低速运行时会出现转矩脉动、振荡和噪声,这显然不符合二维运动机构的技术要求。因此本文拟通过把自适应细分技术(可变细分)引入到加减速控制中,来解决上述问题,实现二维机构在宽速范围下的快速稳定跟踪和扫描。
1自适应细分技术
步进电动机细分驱动的本质是通过对步进电动机励磁绕组中电流的控制,使绕组中合成磁势矢量等幅均匀旋转。在低转速下,细分技术对电机的稳定运行带来十分显著的效果,单个步距角被分为几个微步来完成,以提高电机的运转精度,进而实现步进电动机步距角的高精度细分,有效地遏制了转子的振荡和噪声,因此,细分技术实质上也是一种电子阻尼技术。然而随着电机转速升高,电机转子在前一步振荡尚未到达回摆的最大值时,下一个脉冲就到来,甚至前一步振荡尚未开始就进入了下一步,从而步进电动机的运行如同步电机一样连续、平滑。假若此时依然对电机施加高细分就变得没有太大意义,反而由于细分的电子阻尼作用使电机转速升不上去,此外在高转速、高细分状态下,脉冲频率很高,从而会加重脉冲发生器和环形分配器的工作压力[1]。
基于上述问题,本文提出自适应细分驱动技术,即在不同的转速范围,实行不同的细分驱动模式。为了克服在低频时步进电动机的转矩脉动和噪声大的缺点,使电机工作在高细分状态下;随着转速的升高,电机的转动逐渐趋于连续、平缓,细分数开始逐级减小[2]。因此自适应细分策略是,低转速高细分,高转速低细分,并且细分驱动主要集中在低转速区,细分数的切换在低转速区也相对频繁,具体在不同转速段对应多大的细分,跟步进电动机的类型和参数有关,也跟带载情况有关,需要实验测得。本系统根据电机的参数及动态特性,在保证电机平滑运转的基础上,测得转速范围和细分数的对应关系如表1所示。

表1 转速细分表
2基于自适应细分的步进电动机加减速控制算法
传统意义上,对步进电动机加减速控制的研究重点都停留在加减速曲线的选择,或是基于某种曲线的加减速控制算法的编制和优化上,而且大部分是基于整步状态或固定细分状态的前提下进行研究的。在上述控制方法下,电机可能出现工作在高转速、高细分状态的情况,或出现工作在低速、低细分状态的情况,这显然与引入细分技术的初衷是相悖的,也不符合电机稳定运行的要求;另外,在一种固定细分下进行加减速,机构很可能在某一范围遇到系统的共振点,而在变细分情况下,系统的脉冲频率只在很小的范围内变动,遇到共振点的几率会大大降低,因此对步进电动机加减速控制算法的研究应该在自适应细分的基础之上进行。
本算法首先要实现自细分驱动技术,它独立于加减速过程,并且具有高优先级。在加减速过程中,由于加减速时间非常短,则细分数切换的响应速度需要更快,这就要求自适应细分程序有良好的实时性。本系统利用TMS320F2812的CUP定时器(Timer0),把转速细分表编制到该定时器中断子程序中,并将中断时间设为微秒级,保证算法响应的快速性和细分切换的及时性。
其次是加减速曲线的选择,步进电动机的加减速曲线常用的有匀加减速曲线、指数规律加减速曲线和S型加减速曲线。由于指数规律加减速曲线与步进电动机的矩频特性曲线接近,因而是本系统的理想选择。系统按指数曲线加减速时,脉冲频率f与时间t的关系如下:

式中:fm是步进电动机的最高运行频率,τ是决定升速快慢的时间常数,其数值可由实验测得。若步进电动机运行频率为fn,则由式(1)可算出升速时间:

为了实时性的要求和编程方便,并不按照上式计算加速时间,而是对指数曲线进行离散化,离散后的速度并不是一直上升的,而是分为很多速度等级,加速轨迹呈阶梯状,且每上升一速度等级都要在该等级上保持一段时间,使电机加速充分。步进电动机在每个速度级保持的时间用电机步数表示,本系统把电机加速曲线离散化为12等级,如图1所示。
在编程之前,做了大量实验,根据指数离散化方法,同时结合电机参数特性,对各个速度等级进行逐级调试,测算出在每个等级停留的时间并换算成步进电动机步数,最终得到每个速度等级对应的加减速曲线数据,并将每个速度等级对应的步进电动机在整步状态下的频率值和步数制成表[4]。本系统离散化后的数据如表2所示。

图1 指数离散化曲线
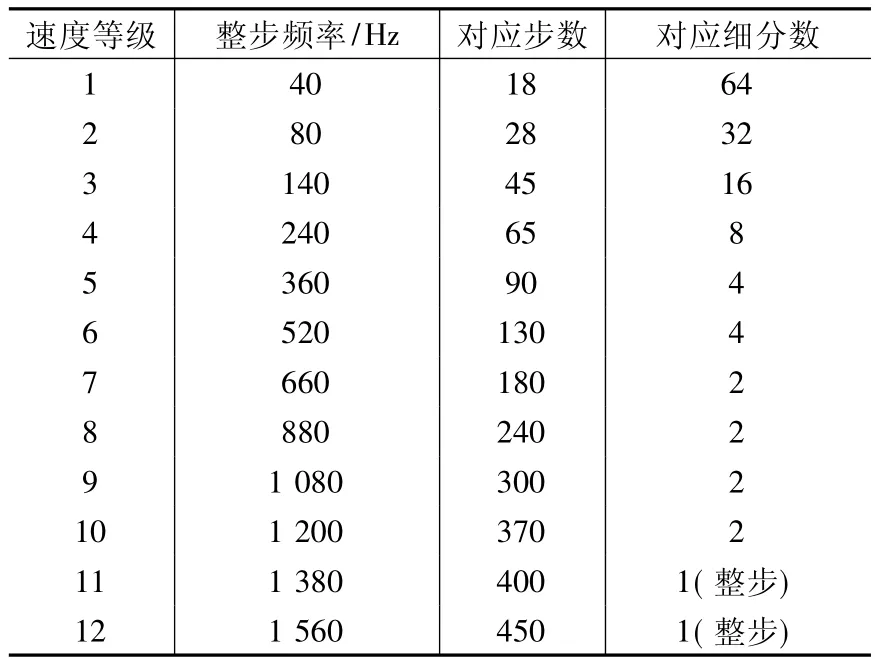
表2 指数曲线离散化数据表
执行加速控制时,根据每级的整步频率和当前的细分数,计算出脉冲频率,并送入DSP的定时器周期寄存器中,再查表找出该速度等级对应的电机步数,计算出该级总的脉冲个数并送入定时器的相关寄存器中,当步数减至零时,表明该等级已经走完,进入下一等级。以上是电机加速过程的处理方法,减速过程的处理同加速过程。
3加减速算法的系统实现
3.1硬件系统设计
控制部分以 TI公司定点 DSP芯片TMS320F2812为核心,DSP通过RS232接口与上位机进行通信,并接收X、Y维电机的起停、正反转以及速度信号。TMS320F2812根据当前的速度信号判断并确定细分数,通过I/O接口发送到驱动电路中,即可实现自适应细分功能[5]。
驱动部分采用两套完全相同的功率器件分别控制X维和Y维电机。功率器件采用由美国NS公司生产的集成驱动模块LMS18245,它内部集成了一个4位的D/A转换器、过流传感器和一个H桥功率输出电路,大幅减少了功率部分的外围电路,因此可以很容易完成对电机电流的数字控制,实现步进电动机的可变细分驱动。硬件系统机构如图2所示。

图2 硬件系统结构图
3.2 软件编制
根据上述控制方法,软件系统的编制主要集中在自细分功能和加减速功能的实现上。加减速的控制在自适应细分的基础上实现,而自适应细分程序要独立编制,并具有高优先级。本文采用TMS320F2812的CUP定时器中断以实现自适应细分功能,并通过设置一个转速全局变量V来反映当前的速度值,定时器中断子程序对V所在的速度区间进行判断,然后对细分数进行更新。为了保证实时性,定时器周期设为5 μs。细分中断子程序流程如图3所示。

图3 细分中断子程序
步进电动机驱动二维运动机构从一个位置运行到另一个位置的过程中,一般要历经加速、匀速和减速三个阶段,DSP需要根据距离信息,计算出加减速阶段各个速度等级的加速步数、减速步数以及恒速阶段的运行步数。另外,对于短距离运行,电机可能尚未上升到最高转速就需要减速,即没有进入恒速阶段,恒速步数为零。利用TMS320F2812的EV(事件管理器)模块可实现上述算法并控制电机运行,以X维电机为例,将加减速控制子程序放在定时器1的比较中断子程序中,每当比较中断发生时调用该子程序,并按上述算法更新 T1PR寄存器和T1CMP寄存器的值。电机加减速控制子程序流程如图4所示。
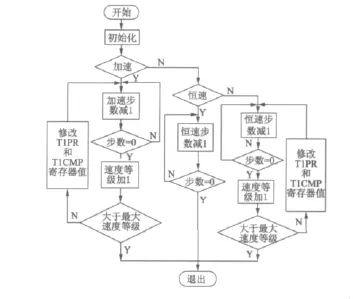
图4 电机加减速控制子程序
4实验及结果
本系统电机选用两相混合式步进电动机,额定激磁电压为28 V,额定相电流为1 A,步距角为1.8°。为了对比自适应状态下与固定细分状态下步进电动机加减速的运行效果,二维运动机构分别工作在这两种状态下,并用示波器记录该过程中TMS320F2812的T1PWM引脚输出脉冲波形,如图5所示。

图5 固定和自适应细分加速脉冲波形对比
比较图5(a)、图5(b)两图可以看出,两种情况下加减速的脉冲波形有所不同。在固定细分状态下脉冲频率是由低逐渐升高,脉冲频率的变化范围在0~3 000 Hz之间。而自适应细分状态下脉冲频率变化范围较窄,大致徘徊在1 500~2 500 Hz之间,图5(b)中频率的跳变是由细分数变化和转速变化共同作用完成的。另外在低速时,由于细分数高,脉冲频率维持在2 000 Hz左右;在高速阶段,尽管速度很高,但由于细分数很低,脉冲频率也依然维持在2 000 Hz左右,这样就大大减小了脉冲发生器和环形分配器的工作压力。试验结果表明,基于自适应细分的加减速控制算法可以实现在加减速过程中细分数的变化,电机在整个转速范围内运行稳定,速度切换平滑,转矩波动和噪声都得到不同程度的抑制。
5结 语
步进电动机的加减速控制在实际应用中具有重要的意义,合理的加减速控制算法可以大大提高步进电动机的运行性能。本文将自适应细分技术引入到步进电动机的加减速控制中,不仅实现了步进电动机的宽速运行,而且在加减速过程中能够实现电机的平稳运行、抑制电机的转矩波动和噪音,也降低了系统对脉冲发生器和环形分配器的要求。并通过实验说明,基于自适应细分技术的步进电动机加减速控制算法可行并且有效,因而具有实际应用价值。
[1] 陈隆昌,阎治安.控制电机[M].第三版.西安:西安电子科技大学出版社,2000.
[2] 赵勇,车建国.步进电机多级细分驱动方法研究[J].江苏电机工程,2003,22(1):23-25.
[3] 常东来.步进化伺服系统输入信号的设计[J].微电机,1999,32(2):24-25.
[4] 李海波,何雪涛.步进电机升降速的离散控制[J].北京化工大学学报,2003,30(1):92-94.
[5] 王瑾.基于DSP和CAN总线的步进电机控制系统研究[J].电子测量技术,2009,32(1):112-115.

