基于Park矢量的电动机轴承故障检测方法

薛征宇，邱赤东，王宁，沈立新

(大连海事大学 a.轮机工程学院；b.交通运输管理学院，辽宁 大连 116026)

三相感应电动机广泛应用于电力拖动系统，其安全性、可靠性、效率等性能一直被电气拖动系统的设计者和维护管理者关注[1-7]。对电动机的故障类别进行统计发现，感应电动机中轴承故障的发生概率为41%，列于首位[8]。这类故障越早发现越好，可以及时更换轴承以有效避免电动机故障进一步恶化。因此对于三相感应电动机的在线故障诊断显得尤为重要。

感应电动机中的轴承故障按照引起故障的部位可以分为分布式故障和局部式故障[9]。振动分析是轴承故障分析的传统方法[4-5,7]，由于故障所产生的振动信号会反应到电动机定子电流中，定子电流易于测量，因此，越来越多的关于感应电动机故障诊断方面的研究，都将关注点转移至定子电流等电信号上[1]。基于定子电流的电动机故障特征分析方法(MCSA),是一种非侵入性的方法，通过分析获取的电动机电流信息来获得电动机轴承运行的有关信息。通过对振动信号的频谱分析和电流信号的频率分析已经获得了振动信号的故障特征频率与电流信号的故障特征频率之间的关系[3]。快速Fourier变换(FFT)是一个非常简单快捷的频域分析方法。但是，由于电动机轴承故障引起的振动能量很低，故障信号往往被电力系统的强噪声背景所覆盖。因此，直接通过传统的FFT频谱分析方法很难判定电动机轴承故障。

近些年来，很多先进的信号处理方法，如小波、小波包分析被应用到故障诊断系统中[10-12]。这些方法计算量大，实现电动机的在线故障监测难度较大[10,13]。在实际供电网络中，电力电子设备经常产生大量的谐波和噪声信号，实际测量的电动机定子电流通常都拥有强噪声背景。最大熵谱估计[14]和多信号分类法(MUSIC)[15]只能够实现高信噪比条件下的故障特征提取；单纯的使用Park矢量法，在处理电网频率频繁波动以及负载频繁波动的情况下对于故障特征频率的提取和判定会出现不稳定。为了克服上述问题，提出一种可用于DSP在线处理的基于Park矢量模的改进聚类算法。

1 Park矢量法

对于三相感应电动机来说，其三相定子电流之和等于零。因此，对于电动机定子电流采集来说，只需要采集两相电流信号即可，另一相的电流可以通过计算获得[13]。作为电动机的三相电流(ia，ib，ic)，可以用Park矢量(id,iq)表示为

(1)

这个变换的优点在于，能够在电流信号中保存所有的信息，而且把3个电流变量转换成2个变量。对于电动机轴承故障诊断而言，仅仅使用Park变换仍不能充分解决问题，因为对于任何一种故障形式，其对应的特征不是唯一的，而且由于体现故障特征的信号比较微弱，特征也不明显，因此，在实际信号中同时考虑噪声等实际因素，信号处理比较困难。为了解决这个问题，使用Park矢量模方法分析这些问题[16]。

在理想条件下，电动机电流为

(2)

式中：if为电动机供电的相电流；fe为基波频率；α为相电流if的初始相角。由于轴承故障而产生的振动导致了电动机定子电流的微弱变化。假定电动机轴承存在故障，并且只考虑电动机定子电流的一次谐波和二次谐波，则电动机定子电流为

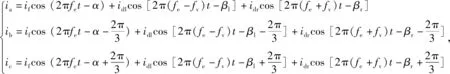
(3)

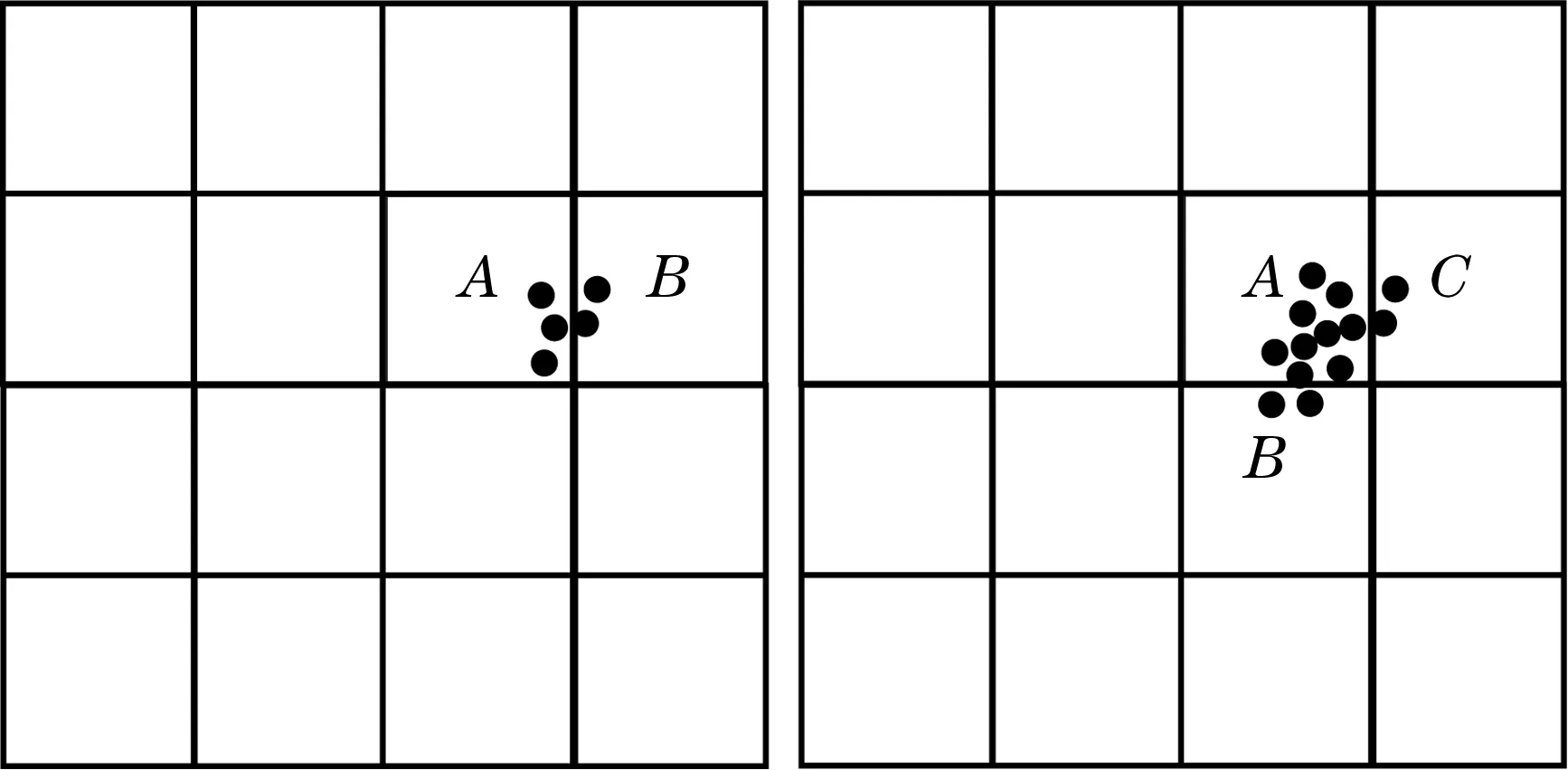
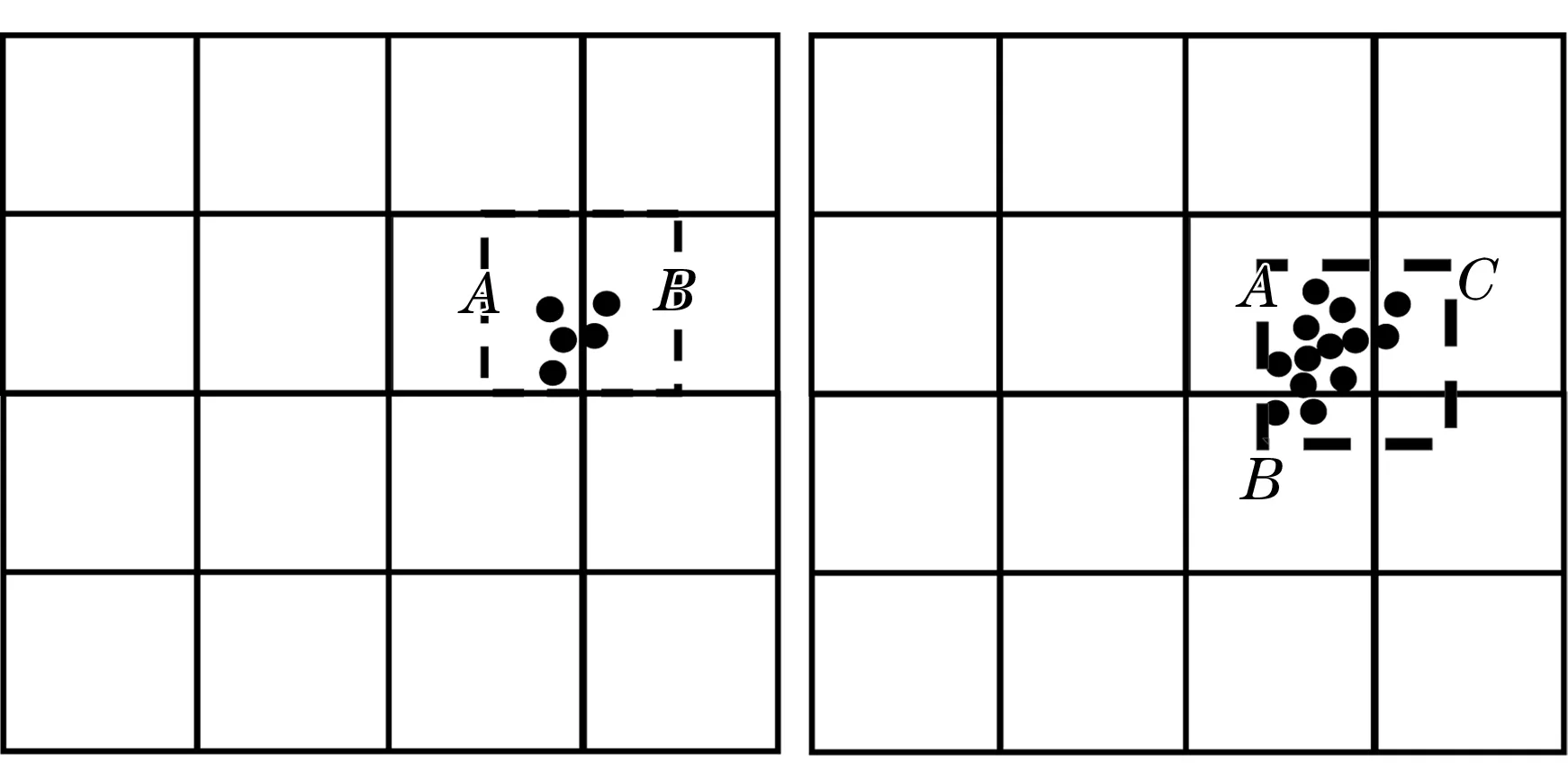
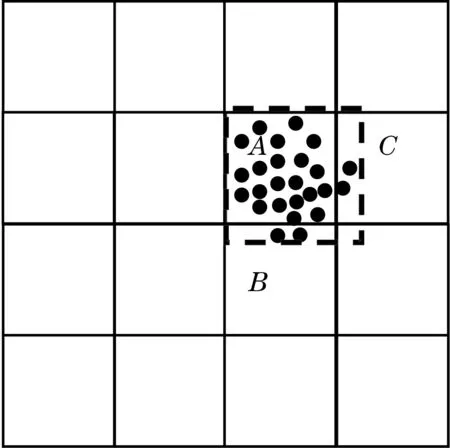
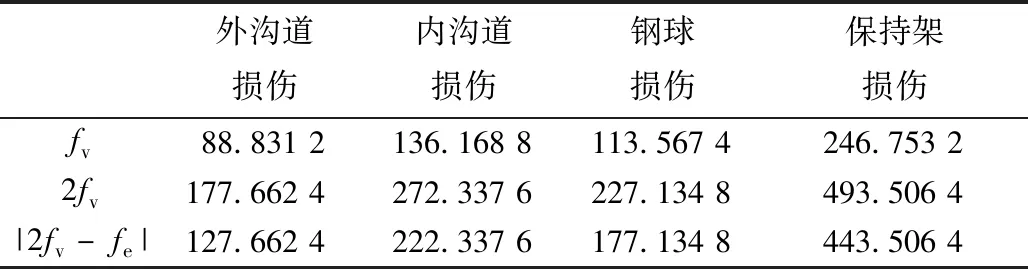
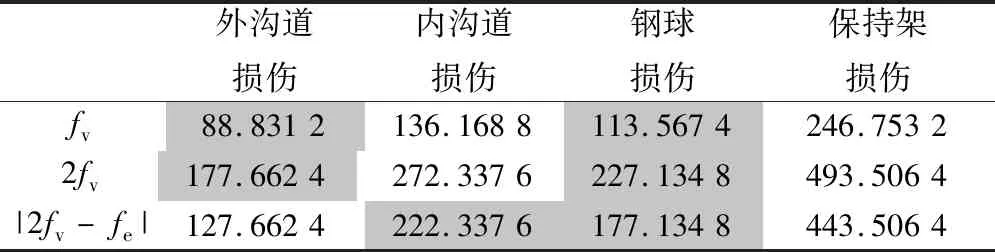
式中：idl为电流低边瓣分量在(fe-fv)下的最大值；fv为特征频率；idr为电流高边瓣分量在(fe+fv)下的最大值；βl为低边瓣分量的初始相角；βr为高边瓣分量的初始相角。 假定轴承故障时fv

cos(2πfvt-α+βl)+3ifidrcos (2πfvt+α-βr)+

3idlidrcos (4πfvt+βl+Br) 。

(4)

从(4)式可以看出，在Park矢量模的频谱中含有主要由电源产生的直流分量和两个谐波分量，其频率分别为fv和2fv。

如果轴承故障时fv>fe，则Park矢量模为

cos(2π|2fv-fe|t-α+βl)+3ifidrcos(2πfvt+α-βr)+3idlidrcos (4πfvt+βl+βr) 。

(5)

类似地，从(5)式可以看出，在Park矢量模的频谱中含有主要由电源产生的直流分量和3个谐波分量，其频率分别为fv，2fv和|2fv-fe|。从上述分析来看，上述两种情况下电源基波的影响可以被屏蔽掉，更加重要是，与电动机故障特征有关的项都被乘以3if，因此故障特征被放大了。

2 聚类算法

聚类分析要求能够自动识别出包含有聚类的子空间。聚类就是将数据对象分为多个类或簇，在同一个簇中的对象之间具有较高的相似度，而不同簇中的对象差别(相异度)较大。通常采用距离度量相异度。聚类不同于分类，分类时，对于目标数据库中存在哪些类是知道的，只要将每条记录分属哪一类标记出来即可；而聚类所要划分的类是未知的，也就是在预先不知道目标数据库有多少类的情况下，希望将所有的记录组成不同的类或者说“聚类”，并且以某种标准度量，在同一聚类之间最小化，在不同类之间最大化。聚类分析的算法可以分为分裂法、层次法、基于密度的方法、基于网格的方法和基于模型的方法[17]。

BIRCH，CLARANS以及DBSCAN等算法[18-20]无法实现寻找原数据空间中包含聚类的子空间。CLIQUE算法能够自动识别包含聚类的子空间，并能够寻找任意类型的聚类[21]。因此，采用该聚类算法实现故障诊断的优点为：可自动发现存在聚类的最高维子空间，而无需用户指定在哪一个子空间中对原数据表格进行聚类分析；能够发现任意形状的聚类；算法所需时间与需处理的总记录数呈线性关系。

2.1 CLIQUE算法的局限性

CLIQUE算法可自动发现最高维的子空间，高密度聚类存在于这些子空间中。CLIQUE算法对元组的输入顺序不敏感，无需假设任何规范的数据分布。其随输入数据的大小线性扩展，当数据维数增加时具有良好的可伸缩性[22]。但是在实际背景应用下存在局限性，主要是密集空间的丢失问题。

CLIQUE算法应用了最小描述长度(MDL)剪枝技术来减少密集单元候选集的数目。该算法通过利用MDL找出在“感兴趣”的子空间中的密集单元，把在同一个子空间中的密集单元分组，并且找出每一个子空间中密集单元选出数据的覆盖。覆盖大的子空间将被选出，其余的将被“剪枝”。如果一个密集存在于k维空间中，那么其在所有子空间映射都是密集的。在自底向上的算法中，为了发现一个k维的密集，所有的子空间都应该被考虑。但是，如果这些子空间在被剪掉的空间中，那么这个密集就永远不可能发现了。使用该方法会产生如下问题：

(1) 如果两个相邻的子空间内有一些密集单元，而在各自的子空间中其又不属于密集单元。在这种情况下，采用最小描述长度剪枝技术选定子空间，会将跨空间的密集单元删除。如图1a所示，图中A与B是相邻的两个子空间，在其子空间中均没有密集单元，若采用MDL剪枝方法，会将A与B都删除掉，这样就会造成聚类结果的偏差。

(2) 如果一个子空间内的密集单元与相邻子空间的点也构成密集，但相邻子空间并不是密集的。在这种情况下，如果采用最小描述长度剪枝技术选定子空间，就会删除一些本应属于密集的单元格。如图1b所示，图中A的子空间中是密集单元，而B与C没有密集单元，但B与A中相邻的元素仍是密集单元，同理C与A中相邻的元素也是密集单元。若采用MDL剪枝方法，会将B与C都删除掉，这样得到的密集单元仍是不完善的，最终会造成分类的不准确。

(a)第1种情况 (b)第2种情况

2.2 改进算法

根据试验结果，令

ζi=2(i-1)/2，

(6)

σi=0.32-0.02i。

(7)

式中：ζ为网格数;i为子空间维数;σ为密度阈值。

随着i的增高，ζ也随之急剧增加，这样会导致在线运行程序时占用大量内存，甚至出现内存不足，而且降低程序运行效率。因此当子空间维数i较低的时候，需要尽量降低子空间候选单元格的数目，这样随着维数的增高，候选单元格数目不至于太大，既能够保证算法的准确性，也不至于因维数的提高导致单元格急剧增长，从而降低程序的运行速度。在网格密度较低的情况下，如果采用最小描述长度剪枝技术选定子空间，可能会漏掉一些密集单元，对最后聚类结果的影响可能会非常严重。因此，在此聚类算法的基础上，提出一种网格平移补偿方法进行密集区域的第2次选择，在二维与三维空间“剪枝”时采用网格平移补偿技术。因为随着维度的增高，网格的密度越高，发生遗漏密集单元情况的概率越低。

该方法的基本思路是：首先利用原来的算法，选出此空间下的密集区域。然后，再选出在相邻的区域内可能会有元素密集的所有区域列表，将这些相邻的区域按照密度阈值进行密集判断。如果有密集区域，再进行单元格的平移，使新的单元格包含所有的密集元素，如图2所示。

(a)第1种情况 (b)第2种情况

在不改变单元格大小的前提下，进行第1次平移。如果单元格的密集程度大到必须要调整其大小时，会根据密集元素的方位与密度阈值动态改变密集区域的大小。这样就避免了等间隔划分网格对聚类结果可能造成的影响，因为网格平移补偿方法不会剪掉密集区间的边缘以及相邻区域内的密集元素,如图3所示。

图3 扩展修正后的效果

3 故障诊断的验证试验

试验采用一台额定电压380 V，额定电流5.7 A，额定功率3 kW，额定转速1 450 r/min，频率50 Hz的三相两极感应电动机，该电动机所使用的轴承型号为6206。将轴承中的某个钢球破坏取出，预设为故障。

该电动机三相电流的数据采集由电流互感器接相应接口，最终接入TMS320F2812 DSP开发板，采集的数据经过Advantech PCI-1712型数据采集卡验证可靠。根据电动机的轴承型号，通过文献[8]所介绍的公式计算出轴承故障反映到定子电流中的调制效应频率，见表1。通过采样数据以及(3)式和(5)式，可以计算出Park矢量模，对其进行快速Fourier变换，然后用改进的聚类算法进行分析。

表1 定子电流调制效应频率 Hz

由于振动特征频率的波动和电动机负载的变化，故障特征频率通常也会动态变化。如果使用没有改进的CLIQUE算法对采集的数据进行数据聚类，由于故障信号比较微弱，故障数据可能被视为非密集单元而被忽视，而使用改进的算法，在很大程度上会减少故障数据漏判的可能性。同时，本算法中单元格的密度和密度阈值，可以根据大量的试验数据分析进行重新设定。

对于采集的数据，使用FFT算法进行了处理，同时采用改进的聚类算法对数据进行分析聚类，聚类算法的具体描述如下：

判定临近子空间的密集单位

Define Di, Ai；

Define N； 数据集中数据点的数目

Define Width； 每个间隔的宽度

Define ；密度阀值

Define CellsList；以二维链表的形式记录的网格，在进行网格的遍历时，采用先横向链结点再纵向链结点判断的策略

Add_Grid_Sets(Ai)；

Begin； 将Di划分到间隔为width很小的网格中

For K= CellsListFirst to CellsListLast step1；从第一个网格到最后一个网格遍历

Begin；

For CellsListCurrent to CellsListNext step 1； 当前网格到与其相邻的网格逐个遍历

Begin；

If(K<=σ&& ( K-1) <=σ)；

If ( (K-1) !=NULL && K!=NULL)；

If ( AdjacengCell(K， K-1))；

CellsListRemove(K-1，K)； 删除聚类小于密度阈值，且单元格平移后仍然不是密集的平移网格

If (K>σ&& ( K-1) <=σ)；

If ( (K-1) !=NULL)；

If ( AdjacengCell(K， K-1))；

CellsListRemove(K-1，K)；删除本格聚类大于密度阈值，但单元格平移后不是密集的平移网格

End；保存原网格划分密集，经过单元格平移后仍然密集的平移网格单元

End；保存原网格划分不密集，但是经过单元格平移后密集的平移网格单元

End；保存原网格划分密集的单元

改进算法前、后的诊断结果对比见表2。由于振动特征频率的波动和电动机负载的变化会导致故障特征频率动态变化，因此每组数据的聚类频率也是动态变化的，表2给出了多次试验所产生数据聚类的频率范围。

表2 聚类算法改进前、后对比表

每次采样有4 096组数据。为了提高计算速度，将这些数据分为8份，每份512组数据。运用改进的聚类算法，通过DSP在线计算，根据表2改进后算法的数据聚类情况与表1事先设定的轴承钢球故障的特征数据对照，聚类结果见表3中阴影部分。轴承故障为钢球损伤，同时结果还显示，伴随有外沟道损伤和内沟道损伤，这是因为由于轴承缺损一个钢球，其外沟道和内沟道的状态也跟正常轴承有所不同，试验结果与表1中钢球故障的理论特征数据基本上是吻合的。

表3 故障轴承在线检测结果 Hz

4 结束语

通过改进CLIQUE算法的剪枝方法，对电动机定子电流进行在线检测，通过DSP对于采集的数据进行计算处理和数据挖掘，从而提取故障特征信息。试验结果表明，所提出的故障诊断的方法在感应电动机轴承故障在线诊断方面是可行和有效的。