基于fluent的气体止推轴承出口性能仿真与分析

王莉娜，刘波，张君安

(西安工业大学 机电工程学院，西安 710032)

弹性均压槽气体静压止推轴承具有高刚度、高精度、高清洁度及低摩擦阻力等特点，在数值仿真中[1-2]，为简化模型，常忽略壁面粗糙度对气体轴承性能的影响，且认为模型出口处的压力为0.1 MPa，这些假设可能引起一定的误差。

因此基于有限体积法的流体动力学软件fluent，对气膜出口处流域进行了仿真计算，并采用层流和湍流模型进行对比。由于气体轴承的工作表面不可能绝对光滑，所以在采用湍流模型仿真的过程中，对壁面粗糙度进行了设置，使仿真结果更趋向于真值。

1 物理模型与仿真模型的建立

1.1 物理模型

含有弹性均压槽的矩形气体静压止推轴承如图1所示，该气体轴承由滑块本体和弹性薄板组成，弹性薄板上的矩形跑道即为弹性均压槽，含有弹性均压槽的气体轴承可以显著提高轴承的刚度及工作稳定性[1,3]。

1—节流孔；2—滑块本体；3—气腔；4—弹性薄板；5—进气孔；6—上顶盖

1.2 fluent仿真模型的建立

1.2.1 二维层流模型的控制方程

根据边界层的特性，对连续性方程和N-S方程(Navier-Stokes Equations)进行简化，得到适合层流边界层内流动的基本微分方程为

式中：u,v为速度矢量沿着x,y轴的速度分量;p为压力。其边界条件为：在y=0 处，u=v=0;在y=δ处,u=v(x)。

1.2.2 二维湍流模型的控制方程

湍流模型很多，在此采用单方程(Spalart-Allmaras)模型，在各向同性的前提下，其二维微分表达式为

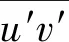
2 网格划分与边界条件的设置

2.1 仿真区域

用fluent仿真时，使用前处理软件gambit建立网格模型(图2)，该模型主要分析从弹性均压槽的位置至气体轴承边缘这部分区域气膜压力分布情况。由于弹性均压槽的尺度比气膜间隙高出一个数量级，所以可认为均压槽内压力处处相等。

图2 用gambit建立的仿真网格模型示意图

传统数值仿真气体轴承时，假设气膜出口处的压力为0.1 MPa，而实际上气膜出口处的压力略大于0.1 MPa。此处在借鉴三角翼外部扰流问题解决方案的基础上，对气膜出口处流域进行了类似的设计，即在气膜出口处建立一个长、宽为气膜间隙数十倍甚至上百倍的大矩形。

2.2 网格划分

为了提高网格的质量[4]，对于带有弧线段的面域(图3a)，须设法构造逻辑四边形，即要在弧线段边界上添加节点，然后设置4个节点均为end，每2个节点之间的线段为side，这样就很容易控制不规则区域的大部分区域，生成质量较好的结构性网格。对于不规则区域余下的弧线段与直线段组成的狭长区域，必须把2个尖角处的节点设置为T，然后采用非结构形网格中的Quad/Tri网格进行划分，在狭长的尖角位置会自动生成三角形网格，其余部分均自动生成四边形网格。

形状规则的区域，只需按照要求设置边界节点个数，就可以控制网格单元的形状(图3b)。这样划分出来的网格，在圆弧面和矩形面之间可以实现很好的衔接与过渡，生成的网格质量较好。

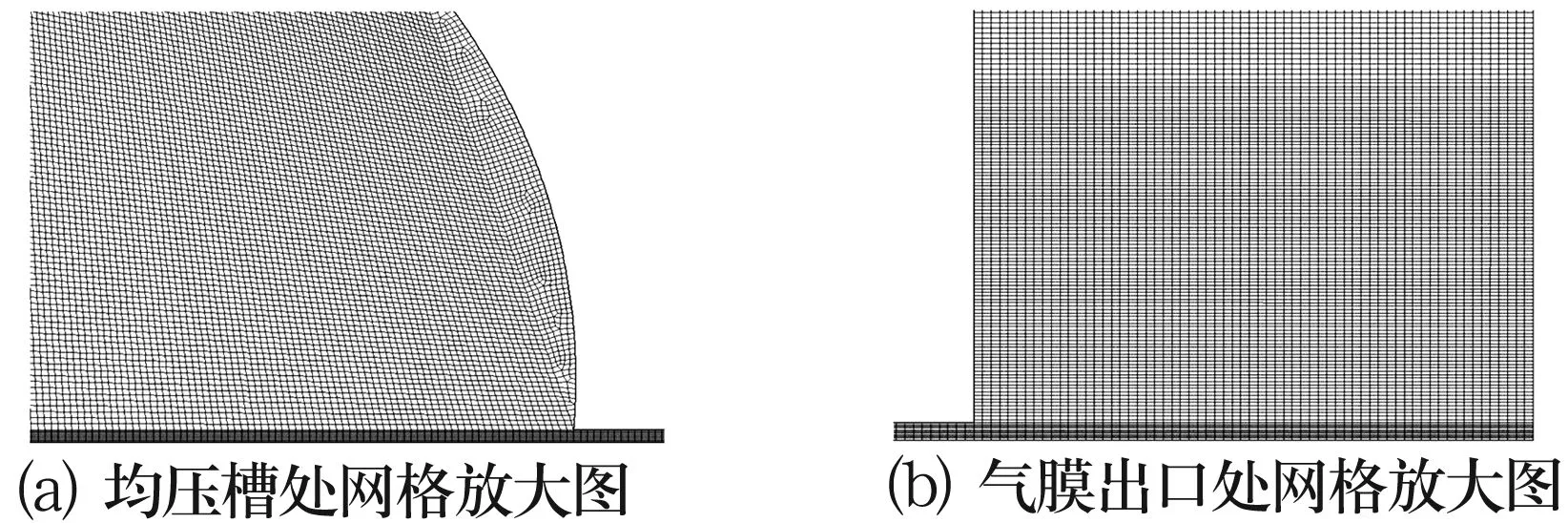
图3 网格局部放大图

2.3 边界条件的设置

采用层流模型时，设置进、出口处的边界条件分别为pressure-inlet和pressure-outlet。气膜出口处往外延伸一个大矩形区域，是因为刚从气膜出口处流出的气体压力肯定比0.1 MPa大，所以在大的矩形区域里，需要重新设定新的压力出口边界,将其压力设置为0.1 MPa。

在考虑固体壁面wall的粗糙度时，需要采用湍流模型，因为只有在湍流模型里，才能够设置壁面wall的粗糙度。湍流模型选用Spalart-Allmaras模型，该模型是一种相对简单的单方程模型，仅考虑了动量的传递方程，专门用于处理具有壁面边界的空气流动问题。在气体动力学中，对于有固壁边界的流动，利用Spalart-Allmaras模型计算边界层内的流动以及压力梯度较大的流动都可得到较好的结果。

3 仿真与分析

3.1 迭代收敛性的判断

使用fluent软件求解流场，观察残差曲线(图4)是判断收敛的常规方法。大多数情况下残差下降4个数量级(即收敛精度为10-4)，且入口流量和出口流量有2个及以上有效数字相同时，就可以认为计算已经收敛。

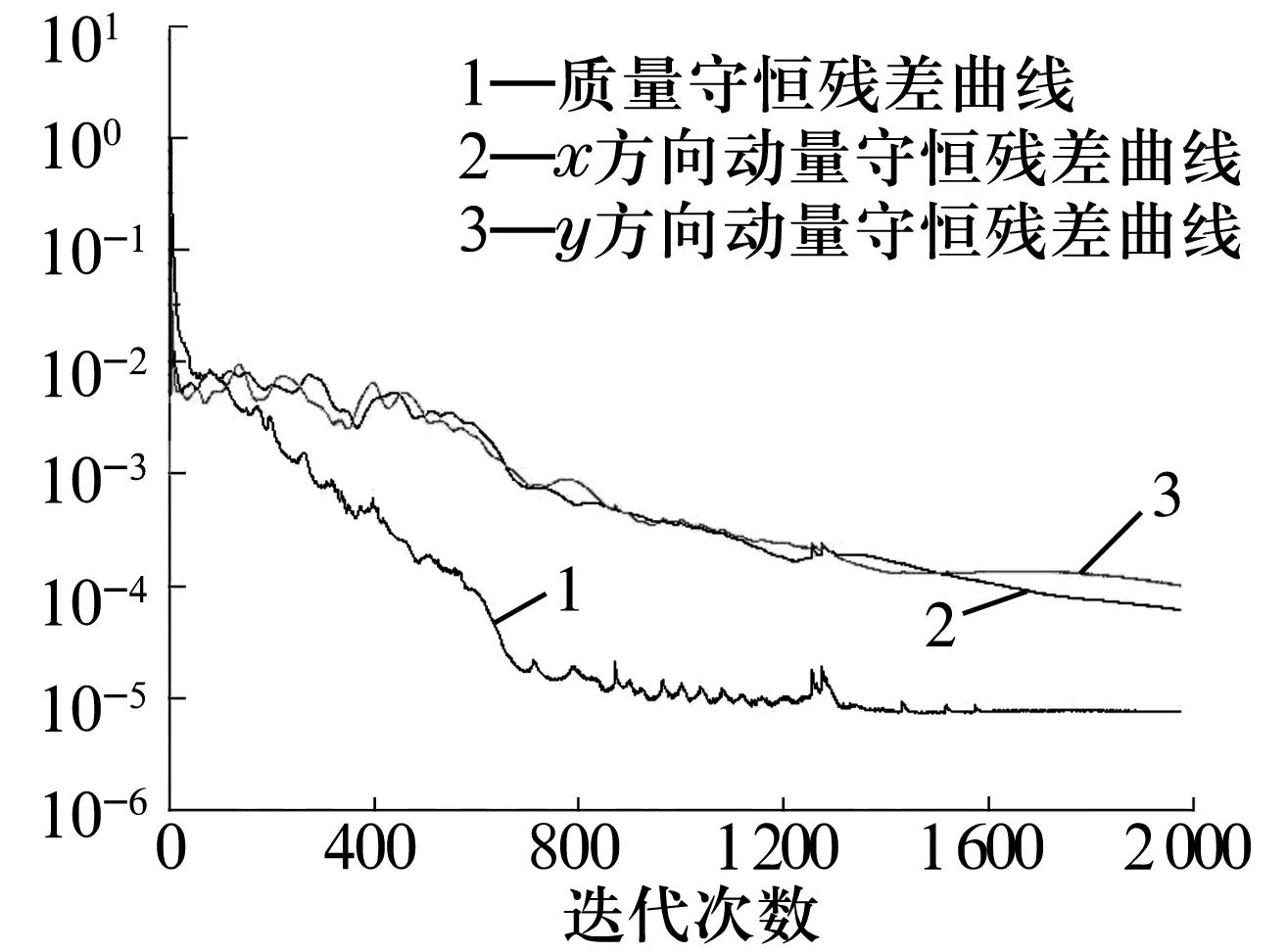
图4 残差图

3.2 仿真结果

不同气膜间隙下，气体轴承边缘气膜压力仿真结果见表1。由于轴承边缘处的出口压力是一系列相差很小的不同的压力值，所以在轴承边缘气膜出口边界上分别选取5个不同的压力值，然后求和取其平均值。

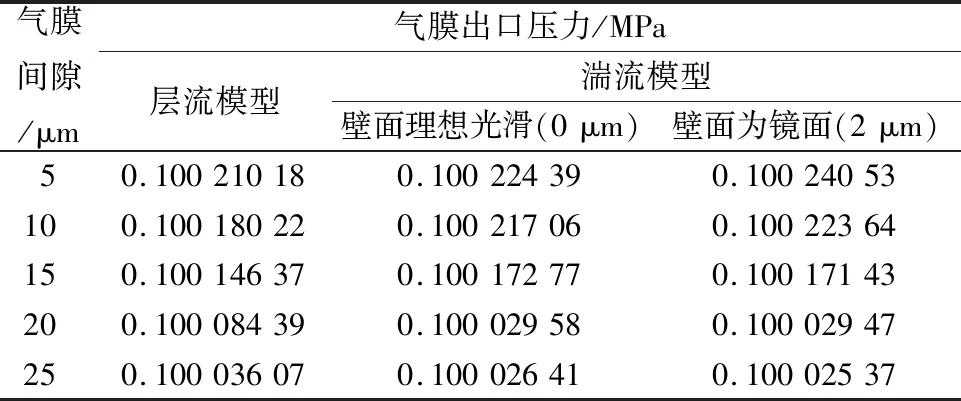
表1 fluent仿真结果

观察气体轴承气膜压力及速度分布云图可以看出：弹性均压槽处的压力基本不变，这是因为弹性均压槽的深度比气膜间隙要高出一个数量级的缘故。而从均压槽边沿到轴承边缘处的压力分布呈逐渐递减的状态，且在轴承边缘处的压力几乎变为0.1 MPa。

在均压槽和大矩形的区域，气体流动速度不大。但在气膜间隙里，由于壁面间隙非常狭小，所以紧挨壁面的速度稍小，而中间层的气流速度非常大，类似于生活中常见的流动的自来水在突然遇到狭小区域时所呈现的现象。

层流模型和湍流模型仿真的结果如图5所示，可以看出气膜出口处的压力值随着气膜间隙的增大而缓慢减小。在气膜间隙小于15 μm时，湍流模型仿真的结果比层流模型仿真的结果稍大；当气膜间隙大于15 μm时，湍流模型仿真的结果比层流模型仿真的结果稍小，并随着间隙的不断增大而最终趋于一致。

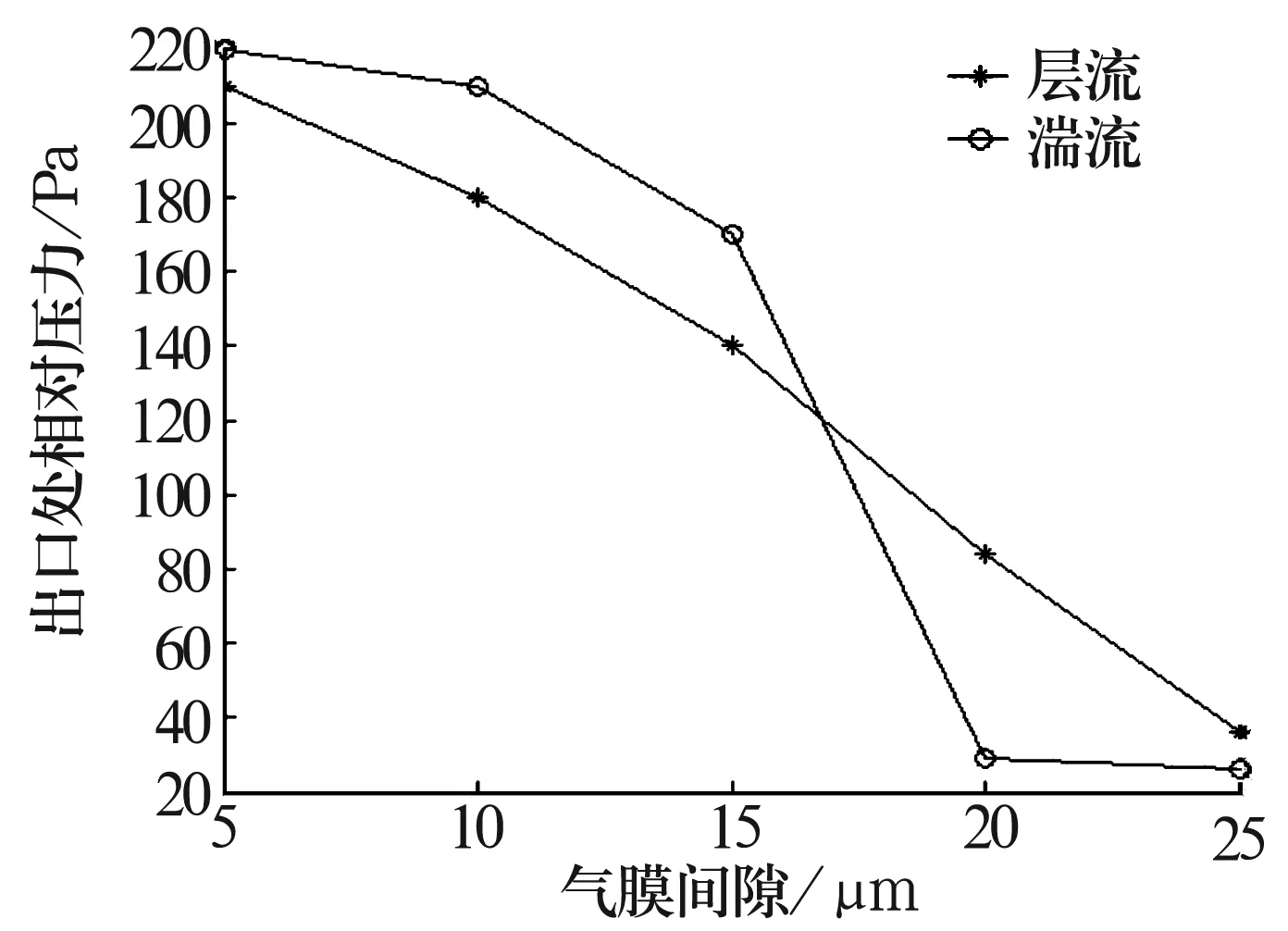
图5 理想光滑壁面时不同模型气膜出口处压力随气膜间隙变化的分布曲线

用湍流模型进行仿真的时候，可以仿真壁面粗糙度对气浮轴承性能的影响(图6)。通过仿真结果可以看出壁面粗糙度会导致气体轴承中的压强分布呈现一定的非线性。当气膜间隙小于15 μm时，壁面粗糙度起到了一定的泄气作用，使得其仿真的出口压力比理想光滑壁面情况下仿真出的结果稍大；当气膜间隙大于15 μm时，壁面粗糙度的影响几乎丧失，此时的壁面粗糙度对气膜间隙内的气体流动形成一定的阻抗，使得其气膜出口的压力与理想光滑壁面情况下仿真的出口压力值相近；当气膜间隙增大到20 μm的时候，壁面粗糙度对气膜间隙内的气体流动几乎没有影响，两种情况仿真的结果趋于一致。

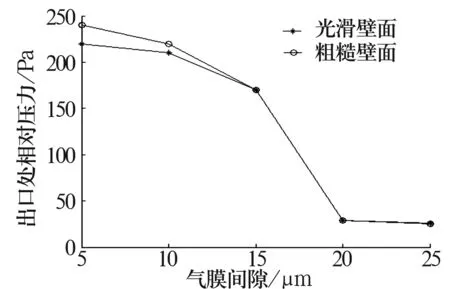
图6 湍流模型下壁面为理想光滑和镜面时气膜出口处压力随气膜间隙变化曲线

4 结论

(1)在传统数值仿真时，假设气膜出口处压力为0.1 MPa，与用fluent仿真的出口处压力值误差为0.02%～0.04%，误差范围很小，可以认为传统数值仿真时假设气膜出口处的压力值为0.1 MPa是正确的。且在气膜间隙很小的情况下，传统数值仿真时假设气体流动为层流状态也是正确的。

(2)在传统数值仿真时，没有考虑壁面的粗糙度对轴承性能的影响。用fluent仿真的时候发现壁面粗糙度对气体轴承性能影响很小，两者的最大误差仅为0.02%。