基于多传感器信息融合的滚动轴承故障诊断

艾莉，华静

(红河学院 工学院，云南 蒙自 661199)

旋转机械中约30%的故障是由滚动轴承损坏而引起的[1]，其运行状态直接影响着主机的工作性能，因此研究滚动轴承的故障诊断技术具有重要的现实意义。近年来，轴承的故障诊断技术得到不断发展和完善，诊断的有效性也在不断提高。但是，在利用振动传感器采集故障信号时，由于单个传感器的可靠性及数据采集的随机性等原因，所获得的信息往往具有局限性，往往容易造成误判。

多传感器信息融合是近几年发展起来的一门技术，其以多个传感器在任意空间和时间上的互补与冗余信息为依据，经过多方面、多层次的相关、组合等分析处理，得出反映环境信息特征的一致性解释和描述[2]。同时，鉴于粒子群算法在迭代寻找全局最优解方面的优势以及BP神经网络具有良好的非线性映射能力的特点，将基于证据理论的多传感器信息融合技术和粒子群神经网络结合起来。应用粒子群神经网络对滚动轴承进行局部故障诊断，并计算各证据体的基本可信任分配函数，再由证据理论进行融合决策。该方法充分利用多个传感器信息，降低了误诊和漏诊的概率，有利于提高轴承故障诊断的精度和准确性。

1 轴承故障特征量的选取

在轴承故障诊断中，故障特征向量的合理选取是诊断的前提，直接影响着诊断结果的准确性。由于轴承的振动信号中包含着其运行的状态信息，当轴承零件如内圈、外圈或滚动体出现局部故障时，将反映为振动信号频率成分和能量的变化[3]。而通过加速度传感器采集的振动信号的随机性较强，且往往是一个宽带信号。因而将这些振动信号的幅域参数统计计算，以提取能够反映轴承运行状态的特征向量。同时，由于振动信号幅域参数：绝对均值、方差、标准差、有效值和方根均值能够体现出信号的变化，并且可以准确地反映某种故障的变化特征。因此，选择这5种归一化后无量纲的参数作为表征轴承运行状态的特征参量，相应4种运行状态为：正常(1 0 0 0)、外圈故障(0 1 0 0)、内圈故障(0 0 1 0)、滚动体故障(0 0 0 1)，作为证据理论的故障识别框架。

2 多传感器信息融合的故障诊断算法

下文采用2个振动传感器进行信息融合，判定轴承的4种故障类型(正常、外圈故障、内圈故障和滚动体故障)。同时，基于提高故障诊断准确度的考虑，先将各个传感器的检测结果通过粒子群优化BP神经网络算法[4]进行局部诊断，以计算各传感器的基本可信任分配函数值，再由证据理论融合决策。

2.1 粒子群神经网络

在d维搜索空间中，有m个粒子组成一个群体，对每个粒子i(i=1,2，…,m)包含一个速度向量Vi=(vi1,vi2,…,vid)和位置向量Xi=(xi1,xi2,…,xid)。该粒子经历的最优位置记为pi=(pi1,pi2,…,pid)，整个粒子群所经历的最优位置记为

pg=(pg1,pg2,…,pgd)。在每次迭代中，粒子i通过跟踪这2个最优值，按照下式来更新速度和位置。

vid(k+1)=wvid(k)+c1r1[pid(k)-

xid(k)]+c2r2[pgd(k)-xid(k)]，

(1)

xid(k+1)=xid(k)+vid(k+1)，

(2)

式中:w为惯性权因子，使粒子保持运动惯性；c1,c2为学习因子，一般c1=c2；k为迭代次数；r1,r2为两随机数，取值区间为[0,1]。粒子在调整自己的位置时，还受到最大速度vmax的限制。如果对粒子的加速导致其在某维的速度超过在该维的最大速度，则该维的速度就被限制在最大速度上。

为了平衡粒子群算法的全局和局部搜索能力，惯性因子常进行自适应调整。

(3)

式中：wmax，wmin分别表示w的最大值和最小值；k表示当前迭代步数；kmax表示最大迭代步数，通常取wmax=0.9，wmin=0.4。

尽管标准粒子群算法收敛速度快，具有很强的通用性，但其存在早熟收敛问题。借鉴遗传算法的变异思想，在标准粒子群算法中引入变异操作，即对某些变量以一定的概率重新初始化。变异操作拓展了在迭代中不断缩小的种群搜索空间，使粒子能够跳出先前搜索到的最优值位置，在更大的空间中继续搜索。这种方法既保持了种群的多样性，又可提高搜索出最优值的可能性[5]。

粒子群神经网络算法通过粒子群各粒子在其搜索空间内搜索BP网络各层间的权值及阈值。首先，将BP网络的权值、阈值赋予初始值。其次，根据所确定BP网络的拓扑结构，计算出网络的输出值。再次，用粒子群算法搜索出最优位置，使得适应度函数达到最小。在这里，对2个传感器所采集的数据，分别选用标准粒子群算法和带变异操作的粒子群算法进行BP网络权、阈值寻优。最后，采用BP网络对所获得的最优值进行二次学习训练，得到最终的轴承局部故障诊断模型，并将输出结果折算后进行融合决策。

2.2 证据理论

证据理论[6-7]是建立在一个非空集合Θ基础上的理论。首先定义识别框架Θ，其由一些互斥且穷举的基本命题组成。令2Θ是Θ的一个mass函数，在2Θ上，若函数m:2Θ→[0,1]，且满足

(4)

如果A为Θ的子集，且m(A)>0，则称A为证据的焦元，所有焦元的集合称为核，证据由证据体(m,m(A))组成。

设m1和m2分别是识别框架Θ上的mass函数，对∀A⊂Θ，A≠φ，有如下合成规则

，(5)

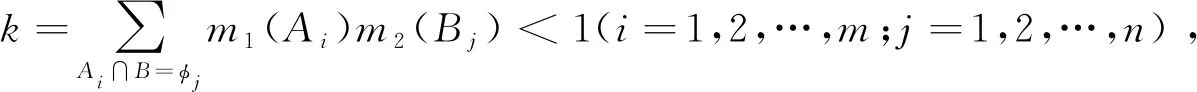
3 仿真试验

在仿真试验中，对轴承进行局部故障诊断所采用的2个粒子群神经网络的结构均为5-10-4，训练误差为0.000 1，置信门限设为0.8。粒子群优化算法的参数设置为：种群规模30，最大迭代次数50，学习因子c1=c2=1.494 45，惯性权重w随迭代次数由0.9线性地减小为0.4。带变异操作的粒子群算法的变异概率p=0.2，Matlab代码为：

If rand>0.8

k=ceil(2*rand);

pop(j,k)=rand;

end

文献[8]给出了轴承4种常见故障类型与振动信号幅域参数之间的关系数据，其中测试数据见表1。在Matlab中编程，可得出带变异操作的粒子群神经网络算法适应度函数变化曲线如图1所示。

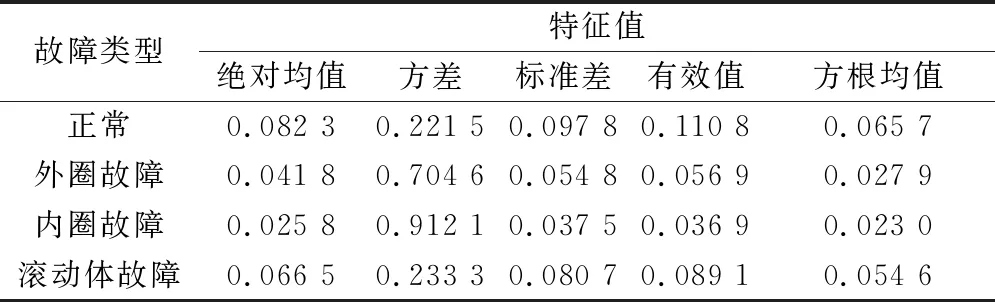
表1 测试数据

图1 带变异操作的粒子群神经网络适应度函数变化曲线

由图1可以看出，当带变异操作的粒子群神经网络迭代16次后，满足了预设精度要求。并且较BP网络而言，粒子群神经网络输出的误差更小、收敛速度更快，这也是选其作为局部故障诊断模型的原因。

为了进一步说明该故障诊断方法的有效性，下面以轴承内圈故障为例进行证据融合。由表1中的测试数据，此时2个传感器输出结果构成的故障矩阵为：

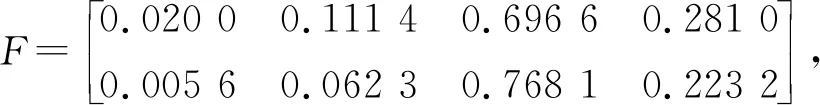
将2个传感器输出结果进行归一化处理，其单独及融合(k=0.316 1)后的可信度分配见表2。其中，m(y1)表示对内圈故障的信任度，m(y2)表示对滚动体故障的信任度，m(p)表示故障类型的不确定度。

由表2可知，传感器1的诊断结果为，内圈故障的置信度为0.628 1，滚动体故障的置信度为0.253 4；传感器2诊断结果的置信度分别为0.725 2和0.210 7；以单个结果看，此时轴承发生内圈故障的可能性最大，但是否出现滚动体故障仍不能完全排除。说明仅仅利用1个传感器信息进行故障诊断时，故障类型识别的不确定性较大。将2个传感器信息融合后，轴承发生内圈故障的可信度值提高到0.850 6，大于置信门限0.8。同时，滚动体故障的可信度下降到0.138 3，而故障类型的不确定度值也大幅下降到0.011 1，表示对内圈故障的支持程度增大了。最终诊断出的故障类型只为内圈故障，与实际发生的故障类型相吻合。

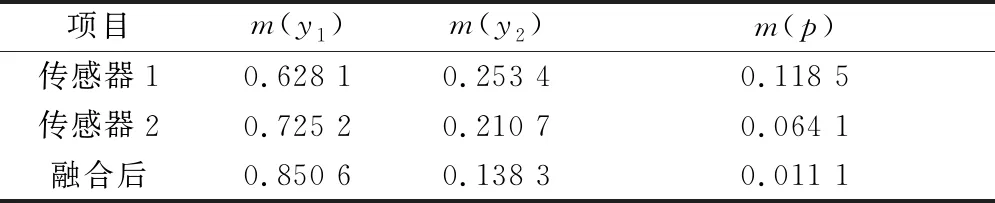
表2 传感器的可信度分配

4 结束语

在局部故障诊断时，粒子群优化算法提高了BP神经网络的收敛速度，改善了其泛化能力。并根据证据理论的证据合成规则，最终实现了对轴承故障诊断的最优决策。示例表明，该算法可使诊断结果的可靠性和准确性得到很大提高。