复杂工况下滚子轴承寿命的修正计算方法
冷钢,王黎钦,郑德志,叶振环
(哈尔滨工业大学 机电工程学院,哈尔滨 150001)
1 前言
航空航天领域中滚动轴承的工况条件比较复杂,比如同时承受径向、轴向和力矩的联合载荷作用;轴、轴承与轴承座之间有较大温度差等。这些因素都影响着轴承的可靠性与寿命,可能导致轴承短时间内发生疲劳失效。
ISO 281—2007给出了最新的滚动轴承修正寿命计算方法
,(1)
式中:a1为可靠度修正系数;aISO为考虑润滑、污染等的综合修正系数。
然而该计算方法基于理想的载荷分布情况对寿命进行计算。同时,原始的Lundberg-Palmgren(以下简称L-P)方法并没有考虑到由过盈配合、热应力等引起的套圈内部周向应力对寿命的影响。
下文考虑了径向、轴向和力矩联合载荷,过盈配合,离心力及温差等因素,在L-P理论的基础上,依据轴承内部载荷分布及应力计算轴承疲劳寿命,并开发计算程序,分析和讨论了以上参数对轴承寿命的影响,为延长航空发动机轴承使用寿命提供科学工具。
2 基于接触载荷分布的寿命计算方法
2.1 滚道寿命
复杂载荷情况下,不但轴承内部载荷分布不同于标准载荷分布,而且沿滚子长度方向载荷大小也发生变化[1]。为考虑复杂工况下轴承内特殊载荷分布及周向应力对寿命的影响,Harris基于额定动载荷理论对原始L-P公式进行了深化。沿滚子长度方向,将接触长度为l的滚道划分为m段。
每段滚道薄片的基本额定动载荷为
(2)
式中:bm为额定载荷修正系数,对圆柱滚子轴承bm=1.1;Dw为滚子直径;Z为滚子数;α为接触角;γ=Dwcosα/Dpw,Dpw为滚子组节圆直径;m为切片数量;式中上面的符号用于内圈,下面的符号用于外圈。
考虑轴承内部载荷分布与滚子边缘应力集中现象,在第k个薄片形成的内、外滚道上,滚子与滚道接触的当量动载荷为
(3)
(4)
(5)
式中:qijk为第j个滚子与内圈滚道上薄片k的接触载荷;qejk为第j个滚子与外圈滚道上薄片k的接触载荷。fk为滚子在第k片薄片上的应力集中系数。
在任一滚道薄片发生疲劳失效后,即认为轴承失效,根据统计学方法,内、外圈滚道的寿命Li及Le可由所有薄片滚道的寿命表示
(6)
(7)
式中:e为Weibull分布曲线的斜率;Qcik和Qcek为内、外滚道薄片的基本额定动载荷。Qik和Qek为内、外滚道薄片上承受的实际载荷。
2.2 滚动体寿命
L-P疲劳寿命试验数据中,滚动体的失效并不常见。然而随着套圈的材质及加工能力的提高,对于目前生产的轴承,经常看到滚道疲劳失效时滚动体也发生了疲劳失效的情况[2],因此在计算轴承整体寿命时有必要考虑滚动体的疲劳寿命。滚子与内、外滚道接触时滚子薄片的寿命为
(8)
(9)
式中:qcijk与qcejk为第j个滚子上第k个薄片分别与内、外滚道间的额定载荷;Qijk与Qejk为第j个滚子薄片k上的实际载荷。
由(8)~(9)式得到的寿命是以单个滚子的转数计量的,而轴承整体的寿命是以旋转套圈的转数计量的,因此需将上述滚子转数转换为轴承套圈的转数。对于运行过程中滑滚比较小的轴承,内圈每转一周时滚子的转数n为
(10)
因此,滚子整体的寿命为
(11)
2.3 轴承整体寿命
在L-P理论的基础上,Harris将滚动体的寿命考虑进轴承的整体寿命中,轴承整体寿命与内圈、外圈、滚动体寿命的关系为
(12)
3 周向应力对寿命的影响
轴承在工作过程中,其与轴的过盈配合和自身的温度变化引起的周向应力也是制约疲劳寿命的因素。过大的过盈配合会增大内圈内部的周向拉应力,从而增大次表面最大剪应力,降低轴承的疲劳寿命[3];因此有必要考虑周向应力对寿命的影响。
由Hertz理论可知滚子与滚道接触处的应力分布,接触表面的Hertz接触应力引起了次表面剪应力τ,Lundberg和Palmgren假设轴承的疲劳失效是由于次表面最大剪应力τmax引起的。最大剪应力与x,z方向正应力存在如下关系[4]
τmax=(σz-σx)/2。
(13)
根据Jones[5]的研究,对于滚动接触表面下的最大剪应力正比于最大Hertz接触应力
(14)

当内圈与轴采用过盈配合时,由过盈配合引起的周向应力改变了次表层最大剪应力τmax,进而影响了轴承内圈的疲劳寿命。根据(13)式,当考虑由过盈配合引起的周向应力时,次表面最大剪应力τhmax为
τhmax=τmax-σh/2,
(15)
式中:σh为周向应力。
假设轴为实心轴且与轴承内圈材料相同,根据弹性力学可推出,由过盈配合引起的轴与内圈之间的接触压强为
(16)
式中:E为材料弹性模量;Δ为过盈量;F为内滚道直径,d为轴承内径。
Zaretsky提出了一种简化的方法来计算由过盈配合和旋转引起的轴承内圈的周向应力[7]
(17)
式中:ν为泊松比;R′=F/Dw。由(16)~(17)式可得内圈周向应力,代入(15)式得到考虑周向应力的最大剪应力τhmax。
根据L-P理论,轴承的寿命与最大次表面剪应力的n次方成反比
(18)
因此,考虑周向应力影响的轴承内圈寿命为
(19)
L-P研究得到n的取值范围为6.9~9.3,在当前的研究中,通常取n=9[8]。 令修正后内圈寿命与之前比值为LR。
因此将过盈配合修正系数应用于(12)式,得到考虑过盈配合的轴承整体寿命为
(20)
4 温度对寿命的影响
轴承在高速转动过程中产生大量的热量,轴承座、轴承及轴的温度均有不同程度的升高,导致过盈量、游隙及材料属性发生变化。在此仅考虑在一定温度范围内(即材料属性不发生变化的情况下),温度通过影响游隙和过盈量而改变轴承的寿命。
4.1 温度对轴承内部载荷分布的影响
随着温度的升高,轴、轴承及轴承座均径向膨胀。由于热膨胀系数不同,导致径向游隙发生变化。同时,轴与轴承、轴承与轴承座之间随着温度的变化,过盈量也发生变化,导致内、外圈因装配载荷的变化而发生变形,并引起游隙的改变。综上,温度为T时,径向游隙GrT为
GrT=Gr0-2(uieT+ubT+ueiT),
(21)
式中:Gr0为初始游隙;uieT为内滚道半径增大量;ueiT为外滚道半径减小量;ubT为滚子直径增大量,uieT,ueiT,ubT可由文献[9]求得。
由此,温度变化导致轴承工作游隙的改变,进而影响轴承内部载荷分布[6],最终使轴承寿命发生变化。
4.2 温度对轴承周向应力的影响
温度引起的过盈量的改变会导致轴承周向应力的改变。根据前述分析,寿命也将发生改变。由于轴承外圈与轴承座大多采用间隙配合,并且根据内、外圈寿命与轴承整体寿命的关系,可以得知外圈寿命对轴承整体寿命的影响较小。因此以下仅讨论轴与轴承间温差对寿命的影响。
假设轴与轴承为同种材料,运行过程中,由于轴承内圈的温度通常高于轴的温度,导致轴与内圈过盈量的减小,由温差引起的过盈量变化为
Δht=adΔT,
(22)
式中:a为钢材的热膨胀系数;ΔT为轴与轴承内圈之间的温度差。则考虑温度影响,修正后的过盈量Δ′可以表示为
Δ′=Δ-Δht,
(23)
式中:Δ为未考虑温度影响的过盈量。
将修正后的Δ′代替Δ代入(16)式,可以求得内圈寿命修正系数LR′,即可以求得考虑轴与轴承温差的修正轴承寿命
(24)
5 计算结果与讨论
基于上述滚子轴承寿命计算模型,使用Matlab开发了寿命计算程序,结合已有的高速轴承动态性能分析软件,以文献[10]中使用的高速圆柱滚子轴承为例,研究了复杂工况下,弯矩、过盈配合、温度对寿命的影响,并与ISO标准算法进行了对比。轴承参数为:滚子直径14 mm,滚子长度20 mm,滚子组节圆直径183 mm,滚子数36,径向游隙0.063 5 mm,弹性模量204.08 GPa,泊松比为0.3,转速为5 000 r/min。润滑油为合成航空润滑油4050。
从图1可以看出,当轴承径向受载较小时,由ISO寿命计算方法得到的疲劳寿命相对(12)式计算出的寿命偏差较大,随着径向载荷的加大,寿命的减少,其误差逐渐减小。这是因为ISO寿命计算方法是在L-P理论的基础上简化得到的[1],在计算过程中将轴承内部载荷分布理想化,其计算结果也相对偏大。因此,在径向载荷较小时,利用基于载荷分布的寿命算法,将得到更为准确的寿命。
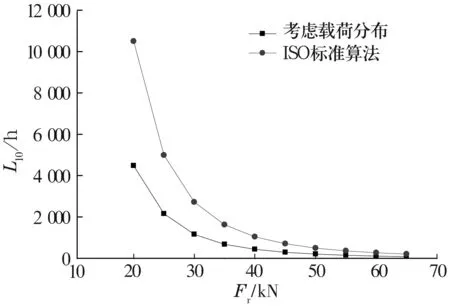
图1 不同计算方法得到的寿命结果
轴承承受的弯矩会引起滚子长度方向上载荷的不均匀分布,利用上文提到的基于滚道薄片的寿命计算轴承整体寿命的方法,可以计算出弯矩对滚子轴承寿命的影响。
利用基于载荷分布的寿命计算式计算得到承受20 N·m弯矩的滚子轴承寿命。并与不承受弯矩的轴承寿命曲线进行对比,发现当径向载荷较小时,弯矩对轴承寿命的影响较大;随着径向载荷的加大,弯矩对轴承寿命的影响逐渐减小,如图2所示。

图2 径向力与弯矩对寿命的影响
利用轴承内部载荷分布,计算出弯矩作用下的轴承寿命。再通过弯矩计算出轴承的倾斜角,得到寿命随倾斜角的变化曲线,如图3所示。轴承在工作弯矩作用下的内、外圈倾斜会使得轴承寿命急剧下降。这是由于工作弯矩引起的轴承承载区域增大和接触载荷显著增加所致。在很小的倾斜角时,采用凸度滚子,能降低滚子倾斜对寿命的影响,这是由于在较小的工作弯矩时,凸度滚子能消除滚子倾斜导致的端部应力集中,改善轴承的载荷分布。

图3 倾斜角与寿命的关系
如图4所示,滚子轴承径向载荷为25 kN时,随着轴与轴承内圈之间过盈量的增大,轴承内圈寿命与整体寿命均显著减小。当过盈量达到0.045 mm时(即内径为120 mm的轴公差为n5时达到的最大过盈量),轴承整体寿命缩短30%。

图4 轴与轴承内圈过盈量对寿命的影响
图5表示在不同过盈量情况下,轴与内圈的温差对轴承寿命的影响。假设轴与轴承的温度不高于150 ℃,轴承钢的材料特性稳定。L′表示考虑温差影响后轴承的整体寿命;L为不考虑温差与过盈时轴承的整体寿命。当初始过盈量为0.05 mm时,温差对寿命的影响较大,温差大于30 ℃时,其导致初始过盈量变为0 mm,即没有过盈引起的内圈周向应力,所以温差再升高也无法导致轴承寿命变化。而当初始过盈量较小时,温差对过盈量的影响较小,因此对寿命的影响也较小。

图5 轴与内圈温差对寿命的影响
6 结论
(1)基于滚子载荷分布的计算模型更为接近轴承的实际工况,相对国际标准中的算法及原始L-P理论算法,能够更精确地预测轴承寿命。
(2)轴与内圈的配合过盈量及温差对轴承的寿命影响明显,不当的过盈量与温差会导致轴承整体寿命的严重降低。
(3)结合高速滚动轴承动力学计算软件[6]和疲劳寿命计算程序能够较好地预测高速圆柱滚子轴承在复杂工况下的寿命,有利于选择轴承最佳工况参数,如轴承最佳径向载荷、过盈量等。

