基于PCA和多元控制图的大坝安全多测点数据监控方法

陈瑞兴,程 琳

(1.中国华电集团公司福建分公司,福建福州 350001;2.河海大学水利水电工程学院,江苏南京 210098)

基于PCA和多元控制图的大坝安全多测点数据监控方法

陈瑞兴1,程 琳2

(1.中国华电集团公司福建分公司,福建福州 350001;2.河海大学水利水电工程学院,江苏南京 210098)

针对大坝单测点安全监控模型存在的不足,提出了一种基于主成分分析的大坝多测点总体监控方法。通过一个线性投影矩阵,对大坝正常运行时的监测数据采用主成分分析计算其主成分,并根据主成分进行数据重构。这样,一方面可以消除噪声的干扰;另一方面通过重构的数据和实测数据计算得到平方预测误差范数,可以方便地实现对大坝状态的总体监控。对于大坝的在线监测数据,采用平方预测误差的控制图和贡献图,可以在测值出现异常时实现对异常测点的定位和异常原因的推断。实例的分析结果表明提出的大坝多测点监控模型具有良好的表现。

主成分分析;SPE控制图;贡献图;棉花滩工程

自从意大利的Faneli和葡萄牙的Rocha[1]等于1955年首次对观测资料采用统计回归的方法进行定量分析以来,大量基于不同理论的大坝安全监控模型被提出来,如统计模型、混合模型[2]、神经网络模型[3]和时间序列模型[4]等。总体而言,这些模型的基本思路都是通过一定方法计算出大坝效应量的预测值并与实测值比较,以判别大坝的工作状况,对其进行监控。但这些模型无一例外的都是单点监控模型。在大坝测点较多的情况下,很容易产生虚报警的问题[4]。此外,监测数据中存在的噪声对数据的分析带来了很大的干扰。

最近出现的大坝多测点监控模型,很好的解决了以上单测点模型的缺陷。如,文献[5]和[6]都采用主成分分析(PCA)方法进行多测点数据的分析;Loh[7]采用自相关神经网络(AANN)的“瓶颈层”来提取数据的非线性主元,并重构环境变量的效应,然后采用重构的误差来进行安全监控。本文在对多测点监测数据进行PCA分析的基础上,采用多元统计分析中的控制图和贡献图实现了多测点数据的监控和异常数据原因的诊断。通过对棉花滩大坝监测数据的分析,证明本文提出的大坝安全监控方法具有一定优势,并可以应用于实际工程中。

1 多测点监测数据的PCA分析

设大坝的某观测物理量有p个观测点x=(x1,x2,…,xp)T。各测点的n个观测样本形成观测数据阵X=(xij)p×n。这p个测点的观测值之间常常具有相关性,这样就增加了样本内部的复杂性。为此,需要寻找r个新变量yj(j=1,2,…,r),使yj满足:

(2)y=(y1,y2,…,yr)的各个分量之间相互独立。

这一过程便被称为主成分分析(PCA)。y1,y2,…,yr称为原多变量监测数据的主成分。

通过PCA,原来的样本数据通过线性投影矩阵A被投影到一个r维的超平面上

其中,Y=(yij)r×n是根据观测数计算得到的主成分数据。采用以下公式对样本数据的协方差进行估算

其中,xj=(x1j,x2j,…,xpj)T是第j个时刻对应的各测点观测样本,u是样本的均值向量。这时,投影矩阵A可以通过对协方差矩阵C进行谱分解而得到

其中,S1和U1代表前r个特征值对应的特征值和特征向量。它们代表的是各种环境变量效应对于协方差矩阵的贡献。剩余的特征值则对应的是环境变量以外,包括观测噪声和坝体结构变化等因素的影响。确定r值时,可以先将p个特征值按降序排列并绘制图形。图形出现第一个突变点时的特征值编号被选定为r。这时线性投影矩阵为[8]

反过来,通过主成分可以重构观测数据

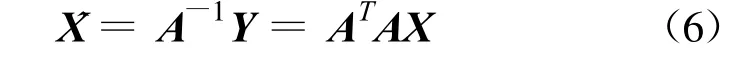
任意时刻j的重构的误差向量为

2 基于多变量控制图和贡献图的大坝健康监控模型

2.1 SPE控制图

对应任意观测时刻j,定义平方预测误差(SPE)范数

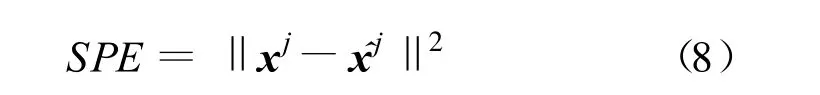
对于任意时刻的观测值,均可以按照上式计算出一个范数来定量的反应环境变量以外因素的影响的大小。大坝正常运行情况下,SPE范数应该在一定范围以内,但当坝体结构出现异常或监测仪器出现故障时,实测数据的SPE范数会超过控制限。

随机变量SPE的分布形式直接关系到其控制限的计算,一般可以假定SPE服从正态分布,进而可以采用正态分布函数来计算其对应的控制限。更为精确的方法是采用Martin&Morris[9]提出的核密度估计(KDE)方法来计算SPE的分布形式。KDE方法采用核函数K(◦)(一般采用高斯型函数)来拟合数据的分布函数。对于一维随机变量的分布函数,可以采用以下形式来进行估计

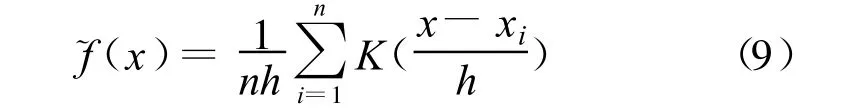
其中,n是样本个数,h为时窗宽度,也被称为光滑参数或带宽;K(◦)是核函数;xi是第i个监测数据。采用上式(9)估算出SPE的概率密度函数后,便可以计算其对应的控制限。仿照正态分布控制限的拟定方法拟定的二级控制限UCL1和UCL2分别是由公式(9)估算得到的SPE的概率密度函数中对应概率为 α1和 α2时的分位值,一般设定 α1=0.95和 α2=0.99。

2.2 SPE贡献图

当监测数据发生异常时,除了能及时的进行报警,还应该对异常的测点进行定位以便对异常情况进行诊断,及时发现大坝的安全隐患并分析出数据异常的原因。这可以通过多元统计过程的贡献图来实现。将观测时刻j所对应的SPE范数重新表达为以下形式[10]

其中,Cspei=(xij-ij)表示在第j个观测时刻,第i个测点对SPE统计量的贡献。对于不同时刻j=1,2,…,n的监测数据,当发生报警时,通过报警时段内Cspe的分布可以推测异常测点的位置。

2.3 监测数据异常原因的定性推断

SPE控制图的四种典型情况见图1。图中情况(c)和情况(d)所对应的SPE控制图均出现了报警。只是情况(c)中SPE在短时间超过UCL2后又减小至正常范围,因此呈现出“V型”的曲线;而情况(d)所对应的SPE曲线则出现了趋势性的增长。

图1 SPE控制图的四种基本情况

贡献图有两种基本的模式,见图2。其中,模式Ⅰ中各测点对应的SPE分量Cspe分布比较均匀,模式Ⅱ中个别测点的SPE分量Cspe明显高于其它测点,有明显的峰值。

图2 贡献图两种基本模式

将观测数据的SPE控制图的四种情况和贡献图两种模式进行组合便可以得到表1所示的六种组合情况Case 1～Case 6。当可以排除人为因素等引起的误测时,可以根据实测数据的SPE控制图和贡献图的组合情况,来对监测项目的状态进行定性的评估。

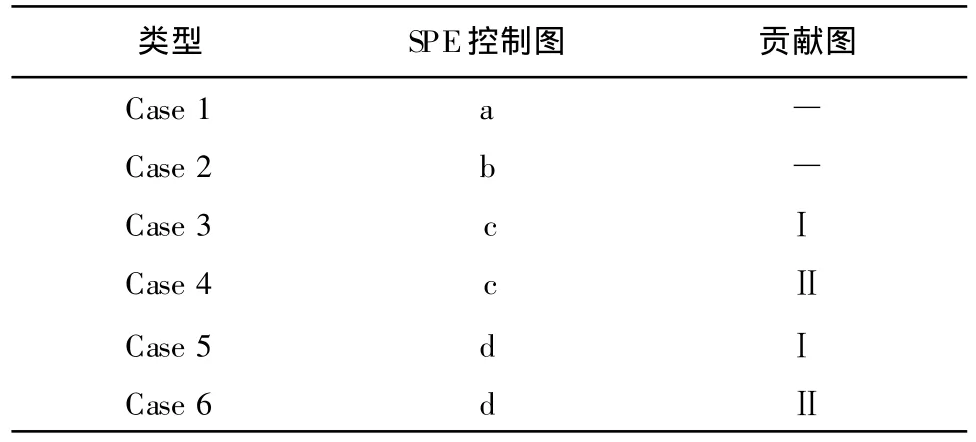
表1 依据SPE控制图和贡献图的可能组合

Case 1:监测数据正常;

Case 2:监测数据基本正常,但需要跟踪监测一两次;

Case 3:监测数据短时异常,贡献图是模式Ⅰ,可能是环境量出现了历史极端情况;

Case 4:监测数据短时异常,贡献图是模式Ⅱ,可能是个别仪器出现故障,后又恢复正常;

Case 5:监测数据异常,并且SPE出现了趋势性增长,贡献图是模式Ⅰ,若环境变量无极端情况出现,有可能是坝体结构出现了较大的时效性变化,应引起注意;

Case 6:监测数据异常,并且SPE出现了趋势性增长,贡献图是模式Ⅱ,可能是因个别仪器出现故障引起的数据异常。

基于PCA和SPE控制图的大坝多测点安全监控的主要步骤如下:

(1)选取大坝安全运行时的监测数据作为参考数据,参考数据要有足够的代表性,能够尽可能广的反映不同环境变量下的大坝效应,然后对参考数据进行标准化处理;根据参考数据采用文中提到的方法计算线性投影矩阵和SPE范数,并采用KDE估算得到的SPE的概率密度函数以便计算其控制限UCL1和UCL2;

(2)对新的监测数据采用参考数据的均值和方差进行标准化,然后采用以上识别的线性投影矩阵来计算数据对应的SPE范数,并与控制限UCL1和UCL2进行对比;

(3)若实测数据的SPE范数超过了控制限,综合采用SPE控制图和贡献图进行异常测点的定位和异常原因的定性分析。

3 工程实例

棉花滩大坝位于中国福建省的汀江干流。大坝采用碾压混凝土(RCC)重力坝,大坝的平面布置见图3。大坝坝顶高程179.00 m,水库的正常蓄水位173.00 m,相应的库容为11.22×108m3,校核洪水位177.80 m。大坝采用引张线来进行水平位移的监测,采用测压管来监测大坝坝基的扬压力情况,引张线和测压管的布置见图4。

图3 大坝平面布置图

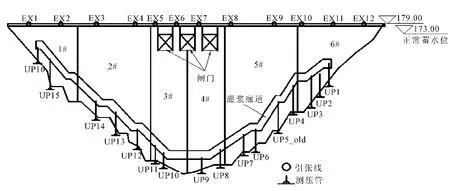
图4 引张线和测压管布置图

3.1 水平位移监测资料的分析

采用12个引张线测点的数据进行分析。引张线监测数据的起止日期为2004年1月1日～2008年3月27日,其中2008年的数据作为在线监测的数据,其它为参考数据。

对参考数据进行分析,其特征值谱见图5(a)。由图5(a)可以看出,特征值谱的拐点出现在第二个特征值处,因此仅需要两个特征值来解释环境变量对监测数据的影响。图 5(b)是由参考数据采用KDE估算得到的SPE的概率密度函数。参考数据和新观测数据的SPE控制图见图6,由图可以看出大坝水平位移监测数据未出现异常,监测数据处于正常范围。

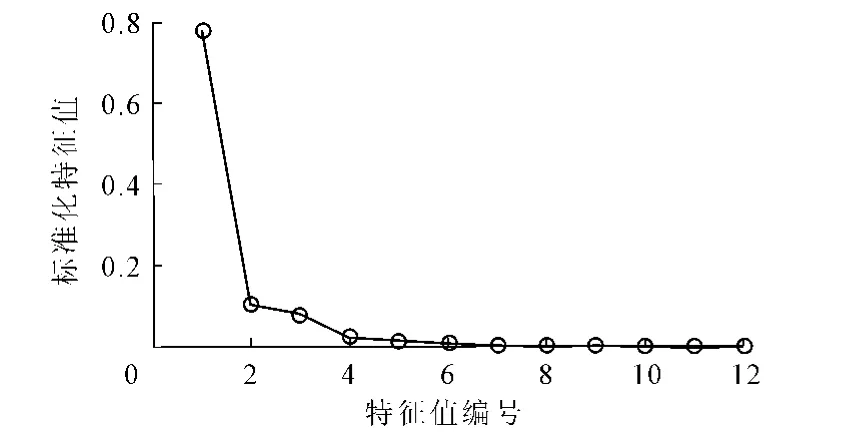
图5(a) 特征值谱图

图5(b) SPE的分布函数图

图6(a) 参考数据图

图6(b) 实测数据的SPE控制图

3.2 坝基扬压力监测资料的分析

对位于坝基纵向基础廊道内的16个扬压力测点,采用2006年 3月 1日～2008年 12月 18日的956个数据进行分析,数据采样间隔为1天。最后56个数据作为新观测数据。图7为新监测数据的SPE控制图,由图可以看出,监测数据的测值出现了报警,SPE呈现“V型”曲线。根据贡献图8可以看出,在测值出现报警的时段内,Cspe集中分布于第5个测点,属于Case 4。据表1推断,测值异常应该是由测压管UP5在短时段内异常所致。根据检查的结果,测压管UP5在该时段内出现了测值异常的情况,后经过处理又恢复正常。

图7 SPE控制图

图8 SPE贡献图

4 结 论

本文提出的基于PCA技术的大坝多测点监测数据分析方法,可以实现对监测数据中噪声干扰的消除。仅通过一个统计量SPE就可以实现对多个测点的同时监控。当测点数据出现异常时,根据多元统计的贡献图还可以实现异常测点的定位和异常原因的推断。相比与传统的单测点监控模型,表现出很大的优势,在大坝安全监测中具有良好的应用前景。

[1]Rocha M.A quantitative method for the interpretation of the resultsof the observationof dams.VI Congress on Large dams[R].Report on Question 21,New York,1958.

[2]吴中如.水工建筑物安全监控理论及其应用[M].北京:高等教育出版社,2003.

[3]Bonelli S,Royet P.Delayed response analysis of dam monitoring data.In:ICOLD European Symposium,Lisse,2001:91-99.

[4]Kim Y S,Kim B T.Prediction of relative crest settlement of concrete-faced rockfill dams analyzed using an artificial neural network model[J].Computers and Geotechnics,2008,35:313-322.

[5]虞 鸿,吴中如,包腾飞,等.基于主成分的大坝观测数据多效应量统计分析研究[J].中国科学(技术科学),2010,53:1088-1097.

[6]Behrouz A N.Multivariate statistical analysis of monitoring data for concrete dams[D].Canada Montreal:McGill University,2002:97-102.

[7]Loh C H,Weng J H,Chen C H,et al.Feature extraction within the Fei-Tsui Arch Dam under environmental variations[J].Nonlinear Stochastic Dynamics&Control,IUTAM BOOK SERIES,2011,29:45-54.

[8]Deraemaeker A,Reynders E,De Roeck G,et al.Vibration-based structural health monitoring using output-only measurements under changing environment[J].Mechanical Systems and Signal Processing,2008,22:34-56.

[9]Matrtin E B,Morris A J.Non-parametric confidence bounds for process performance monitoring charts[J].Statistic process control charts,1996,6(6):349-358.

[10]Miller P,Swanson R E,Heckler CF.Contributionplots:A missing link in multivariate quality control[J].Applied Mathematics and Computer Science,1998,8(4):775-792.

Multivariate Dam Safety Monitoring Model Based on PCA and Multivariate Control Plot

CHEN Rui-xing1,CHENG Lin2
(1.Fujian Subsidiary of China Huadian Group Corporation,Fuzhou,Fujian350001,China;2.College of Water Conservancy and Hydropower Engineering,Hohai University,Nanjing,Jiangsu210098,China)

In view of the shortcomings of univariate monitoring models,a multivariate dam safety monitoring model based on principal component analysis is proposed in this paper.Using a linear mapping,some principal components of monitoring data of the dam under normal operation condition are obtained,and the data is reconstructed from these principal components.Then the disturbance of the noise on the monitoring data could be removed,and the square prediction error which represents the reconstruction error could be calculated and obtained to monitor the state of dam.For the new monitoring data,the SPE control chart and contribution plot are used to infer the reason for data anomaly qualitatively when the abnormal data is detected.The analysis result on a practical engineering shows the good performance of this model.

principal component analysis(PCA);SPE control chart;contribution plot;Mianhuatan project

TV698.1

A

1672—1144(2012)05—0068—05

2012-02-24

2012-04-20

中国华电集团公司科技(创新基金)项目(KJ10-02-22)

陈瑞兴(1963—),男(汉族),高级工程师,主要从事电力生产管理工作。