基于自适应卡尔曼滤波的沉降变形监测数据估计

刘伟诚,王 青,高俊强

(南京工业大学测绘学院,江苏南京 210009)

基于自适应卡尔曼滤波的沉降变形监测数据估计

刘伟诚,王 青,高俊强

(南京工业大学测绘学院,江苏南京 210009)

针对观测数据异常导致滤波偏离的问题,提出了整体控制状态协方差阵自适应卡尔曼滤波方法,通过对某地铁隧道底板结构沉降监测数据进行处理,结果表明整体控制状态协方差阵自适应卡尔曼滤波方法不仅计算简单,而且能有效地控制观测数据异常对沉降变形监测系统参数估计的影响,提高变形监测数据估计的精度。

卡尔曼滤波;自适应估计;协方差;变形监测

变形监测的目的是掌握变形体的实际状态,并通过多期重复观测为判断其安全提供必要的信息,但是现在的变形分析方法多数都是离线的(事后的),无法进行即时预报与监控。卡尔曼滤波是借助于系统本身的状态转移矩阵和观测数据,将参数估计和预报有机结合起来,对变形体进行实时数据处理。其计算过程是一个不断预测、不断修正的过程[1],并且在求解时也无需存储大量观测数据。在利用观测数据进行滤波时,首先需要确切知道系统的初值,但在实际工程应用中,滤波前系统的初始状态是难以精确确定的,因此围绕如何利用当前观测信息和状态估计更新先验信息和补偿状态方程误差,成为工程应用领域的热点问题之一。

在各类工程应用中,基于不同的工程应用背景,国内外学者提出了多种行之有效的自适应卡尔曼滤波方法。这些方法大致可分为两类,一类是方差补偿法[2],在滤波过程中利用已有的信息对观测向量的协方差阵和状态协方差阵进行实时估计。如:基于移动窗口法协方差估计、基于方差分量估计;另一类是函数模型补偿法[3],通过引入附加参数降低系统误差的影响。

在沉降变形监测系统[1,4]中,变形体上布设的一些变形监测点可能会发生突变。由突变引起的观测数据异常将导致卡尔曼滤波估计的误差增大。为此,本文提出利用整体控制协方差阵自适应卡尔曼滤波方法对观测数据进行估计,并结合实例分析,结果表明:此方法能够有效地抑制观测数据异常对卡尔曼滤波估计误差的影响。

1 沉降变形监测系统的卡尔曼滤波模型

沉降变形监测系统是由处于运动之中的一组监测点所构成,这些监测点的位置可看作时间k的函数。为了估计沉降变形监测系统的运动状态,通常以监测点的位置和它们的速率为状态向量。设监测点i在k时刻的高程为Hi(k),其瞬时速率为Vi(k),而将瞬时加速度Wi(k)看作一种随机干扰,即视Wi(k)为动态噪声,则有以下微分关系式:

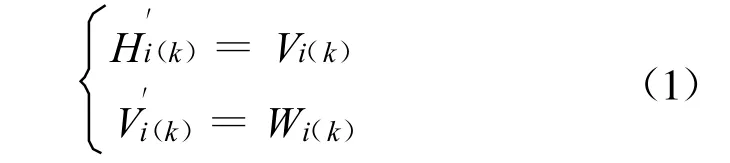
设点i的状态向量为Xi(k)=[Hi(k)Vi(k)]T,则式(1)可写为:

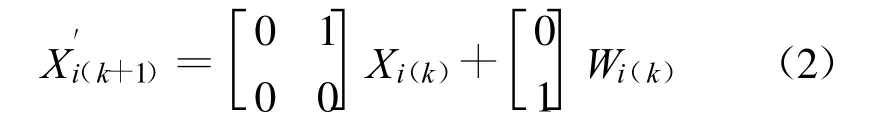
式(2)是一个微分方程,将其离散化可得点i在第k+1期的状态方程[1]:

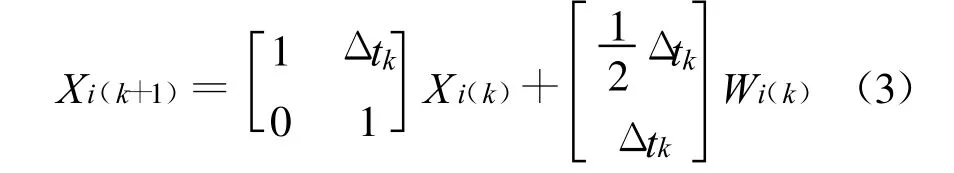
式中 ,Δtk=t(k+1)-tk,而t(k+1)和tk为第k+1 期和第k期的观测时刻。

若记全网q个监测点的状态向量和动态噪声向量为:

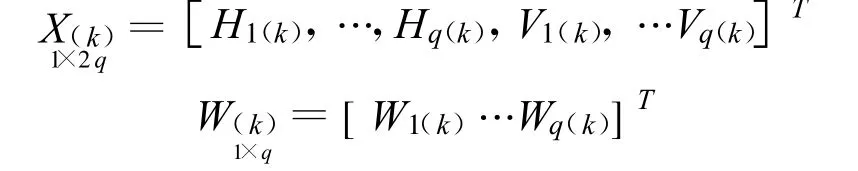
则得到全网在第k+1期的状态方程

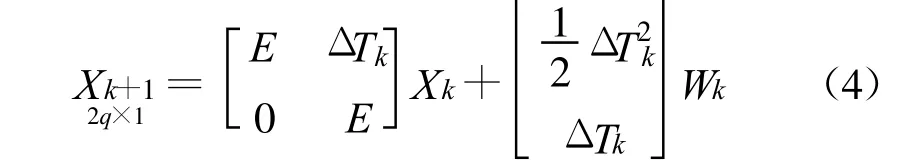
式中 ,0,E,ΔTk均为q阶方阵,且 ΔTk=ΔtkE。

如果认为第k+1期的观测高差都是在tk+1时刻观测的,则hij的观测方程为

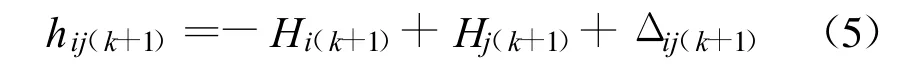
卡尔曼滤波计算过程为:

状态预报

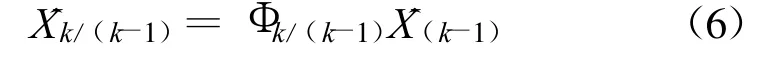
状态协方差阵预报

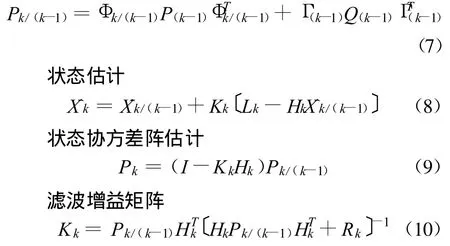
2 整体控制状态协方差阵自适应卡尔曼滤波方法

卡尔曼滤波在利用观测数据进行递推滤波过程中,Pk/(k-1)和Kk值随迭代计算不断趋于稳定值,即滤波器趋于稳定[5]。如果沉降监测点的观测数据中有较大波动的值,那么这些异常的观测数据将会导致滤波偏离。顾及计算过程中观测数据异常,本文提出利用整体控制状态协方差阵自适应卡尔曼滤波方法[6-9]对观测数据进行滤波处理。该方法是根据滤波自身产生的预报残差、滤波残差等信息控制观测数据异常对状态参数估计的影响,以达到最佳的滤波效果。

根据卡尔曼滤波的数学模型可以得到预报残差的表达式为:

如果上式不成立,表明异常的观测数据已破坏滤波器的稳定性,滤波估计结果会出现大的偏离。因此,我们在原状态协方差阵Pk/(k-1)上附加标量因子s对状态协方差进行整体控制。

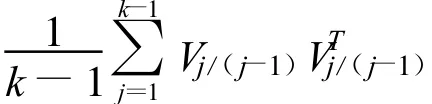
整体控制状态协方差阵自适应卡尔曼滤波方法就是对状态协方差进行区分,对破坏滤波器稳定性的观测数据进行自适应滤波处理,从而降低观测数据出现突变的影响,提高估值的精度,并且此方法判断直接,计算简单,适应性强。

3 实 例

为验证整体控制状态协方差阵自适应卡尔曼滤波方法对滤波偏离的影响,以南京某地铁隧道沉降监测数据为例进行分析。该地铁隧道底板结构沉降采用Leica DNA03电子水准仪进行往返观测,自2010年5月取得初始值,至今已监测30期数据,前17期平均30 d监测一次,后13期平均90 d监测一次。本实例利用等时间间隔的前17期监测数据进行卡尔曼滤波处理。

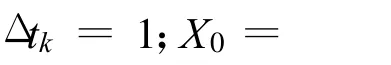
滤波过程分为三步:根据Kk值判断滤波器是否趋于稳定;传统卡尔曼滤波数据估计的获取;通过整体控制状态协方差阵卡尔曼滤波方法获取最优滤波数据估计。

表1 传统卡尔曼滤波结果与监测网平差值对比 单位:mm

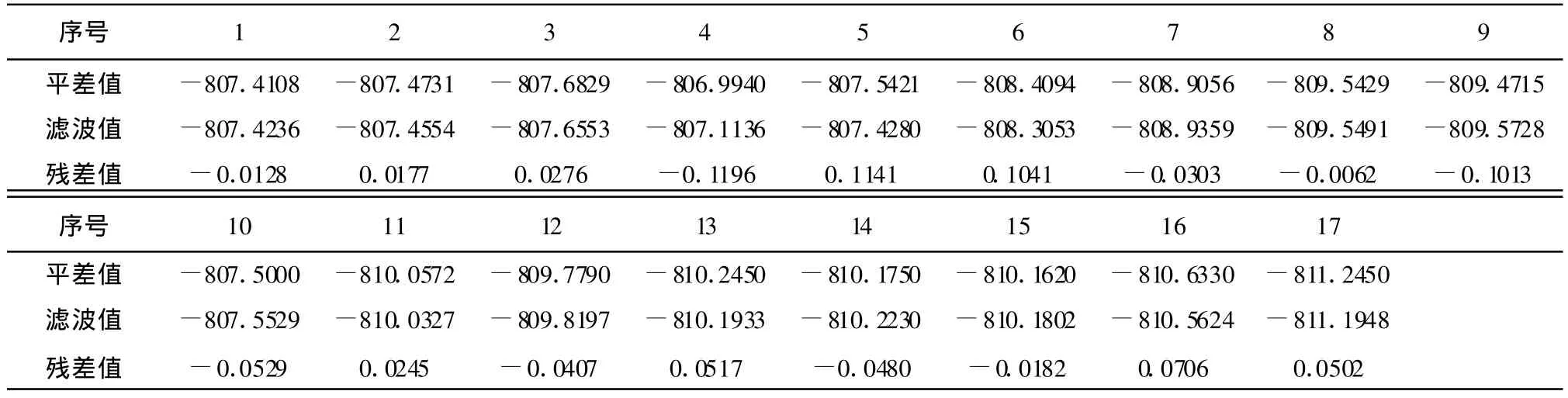
表2 自适应卡尔曼滤波与监测网平差值对比 单位:mm

从表1和表2可以看出,传统卡尔曼滤波值、自适应卡尔曼滤波值与监测网平差值之间的残差值不大,传统卡尔曼滤波值最大残差为0.5552 mm,估计中误差σ=±0.177 mm;自适应卡尔曼滤波值最大残差为-0.1196 mm,估计中误差 σ=±0.06 mm。当监测点的观测数据出现异常时,自适应卡尔曼滤波则充分展现其整体控制能力,滤波残差值波动比较小,而传统卡尔曼滤波的残差值波动比较大,见图1。

图1 传统卡尔曼滤波与自适应卡尔曼滤波残差值

4 结 语

传统卡尔曼滤波克服观测数据异常的能力比较弱,异常的观测数据不仅会影响后面几期观测数据的滤波估计,而且观测数据异常越明显,滤波估值的波动就越大。在卡尔曼滤波过程中,动态模型采用一组状态微分方程和观测方程来描述其变形系统,它把参数估计和预报有机结合起来,其参数是不断变化的,动态不断修正的过程[1,10],从而也不断增强了模型适应变形观测数据的能力,能实时的反映变形体的状态。整体控制状态协方差阵自适应卡尔曼滤波方法简便实用,能有效地控制观测数据异常对动态系统参数估计的影响,保证变形监测数据估计的精度。

[1]崔希璋,於宗俦,陶本藻,等.广义测量平差[M].武汉:武汉大学出版社,2006.

[2]杨元喜,徐天河.基于移动开窗法协方差估计和方差分量估计的自适应滤波[J].武汉大学学报(信息科学版),2003,28(6):714-718.

[3]许阿斐,归庆明,韩松辉.卡尔曼滤波模型误差的影响分析[J].大地测量与地球动力学,2008,28(1):101-104.

[4]陈 健,高井祥.动态水准监测网的数据处理研究[J].矿山测量,2006,(3):21-23.

[5]秦永元,张洪钺,汪叔华.卡尔曼滤波与组合导航原理[M].陕西:西北工业大学出版社,2004.

[6]胡丛玮,刘大杰,姚连璧.带约束条件的自适应滤波及其在GPS定位中的应用[J].测绘学报,2002,(S1):39-44.

[7]夏开旺,石双忠,杨永平.卡尔曼滤波在变形监测数据处理中的应用[J].三晋测绘,2004,11(3):38-41.

[8]Yang Y,He H,Xu G.Adaptively robust filtering for kinematic geodetic positioning[J].Journal of Geodesy,2001,75:109-116.

[10]尹 晖,时空变形分析与预报的理论和方法[M].北京:测绘出版社,2002.

Estimation for Deformation Monitoring Data Based on Adaptive Kalman Filtering Method

LIU Wei-Cheng,WANG Qing,GAO Jun-Qiang
(College of Surveying and Mapping,Nanjing Polytechnical University,Nanjing,Jiangsu210009,China)

In view of the filtering departure problem resulted from the observational outliers,an adaptive Kalman filtering method is proposed based on the robust variance matrix estimation.By the derivation and calculation for the deformation monitoring data of a metro,it is shown that the adaptive Kalman filtering method could not only predigest the calculation process,but also improve the precision of the estimation for deformation monitoring data.

Kalman filtering;adaptive estimation;covariance;deformation monitoring

TU433

A

1672—1144(2012)05—0026—04

2012-03-21

2012-04-20

江苏省测绘局科研项目(JSCHKY200808);江苏省建筑业科研项目(JGJH2008-07)

刘伟诚(1987—),男(汉族),江西吉安人,硕士研究生,研究方向为精密工程测量和变形监测。