上海零售业商务租赁市场的研究

杨 林，高宏霞

（兰州大学 经济学院，甘肃 兰州，730000）

一、引 言

地产方面的研究是非常重要的，因为这关系到地产所有者以及租户的利益，并且，当投资者考虑他们是否要投资时，他们会把租金纳入考虑因素。回顾以前关于租金预测的研究，我们可以发现这方面的研究是非常有限的。零售租赁市场比起其他类型的地产市场，诸如办公写字楼一类要复杂得多，因为有更多的因素影响着零售租金，比如主要租户以及品牌组合。

亚洲的零售市场快速的发展着，大多数的零售空间租赁合同是用一种风险分担方式签订的：用销售额的一定百分比当作租金支付，但是相关的文献几乎无法找到。作为中国最发达的城市，上海已经展现出在零售市场上的巨大潜力。根据中国国家统计局的资料，上海在2010年国内生产总值（GDP）以及人均GDP（分别为15046.45亿元人民币以及78989元人民币）分别是1978年的51倍和32倍。根据Tsola⁃cos（1995）、Hanna et al（2007）、以及 Hendershott et al（2005）的研究，强劲发展的经济是零售业务发展的重要因素。在这个背景下，上海零售业务已经在过去20年中保持了非常强劲的发展势头。如图1所示，上海在2010年全年的零售总额是1978年的82倍。并且，地理知识现在越来越广泛地应用到了城市经济中，尤其是在房地产经济研究中，但是空间计量经济学技术却很少在之前的零售租金研究中使用，在这方面应该做更多的研究以填补空白。

图1 1978—2009年的零售成交量（亿元）

二、文献综述

Sirmans和Guidry（1992）证明了零售物业的特点和位置在租金方面的重大影响。这项研究使用了美国的直观数据。他们的论文中使用了如下的变量：

在这个模型中，解释变量被分为以下四种类型：（1）可变变量：包括区域、租用年限以及主要租户的类型；（2）不可变变量：零售地产的构造；（3）“LOC”：位置；（4）“MKT”：指市场的状况，包括外部设施条件以及经济状况。Huiet et al（2007）也做过香港方面的相似研究，在他们的研究中，零售地产的类型是非常重要的变量，并且还加入了更多的变量，但是容积率被认为是香港市场中并不重要的因素。这一点与Sirmans和Guidry（1992）以及Hardin et al（2001）的研究是相反的，他们的研究专注于美国的零售地产。在他们的论文中，Hardened et al（2002）将容积率作为内生变量，为了研究容积率的解释效力，使用了辅助解释变量以及双阶段模型，此外，还使用了美国的数据库，得出了容积率与租金呈重大负相关的结论。

Jackson（2000）的报告应用了聚类分析技术和来自英国的面板数据的研究以揭示一个更好的零售市场分类，该分类非常具有经济学意义。邻近的零售地产的影响是由Hardin和Wolverton使用横截面数据调查的。为了在零售租金调研中处理空间的自相关，Carter和Haloupek（2000）使用了加权最小二乘（WLS）模型[1]。在该背景下，本文研究上了上海零售空间租金的决定要素。

三、实证方法

（一）OLS模型

普通最小二乘法（OLS）模型用来估计零售租金的决定要素。除了容积率由于缺乏信息而未被选取外，其他所有在Sir⁃mans以及Guidry中讨论的解释变量都得到了选取。构建的模型如下所示：

因变量为Y；自变量为LTA和LRA的自然对数等同于零售租金、总面积以及零售面积；DGi代表了政府的构建区域dummy变量；Tj代表了不同类型的零售；DTCk代表了从该地产到市中心的距离。

在第二个模型中，地区的新分类(Di)是用来设置如下模型的：

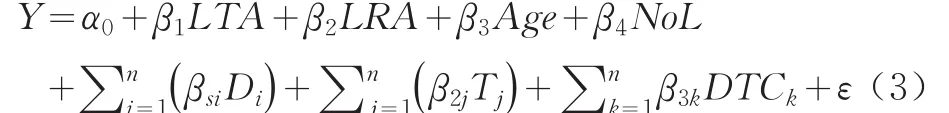
变量TA、RA、Age以及NoL和变量Di、Tj在模型（4）中组合在了一起：

组合变量的系数可以解释为不同地区、不同类型的零售地产性质的边际效应。

（二）空间自相关

一旦空间自相关存在，来自OLS模型的误差项方差就不会在不同地区之间不变，OLS模型在捕捉方差方面会变得不太适当（Anselin，1998），自相关问题可以通过Moran（1948；1950a，b）的统计数据来得到检测。当Moran’I等于0时，自相关问题就不会干扰到预计结论[2]。一旦自相关问题被检测出来，空间可估计自回归模型（SAR）就可以得到预测。为了使用Moran’I测试并且构造SAR模型，应该建立一个对于回归模型是外生变量的空间权重矩阵以检测空间相关性（Manski，1993）。空间回归模型 （Cliff，1981；Anse⁃lin，1988）是按照如下方式建立的：

Y是作为N×1向量而被表达的自变量，W1和W2是权重矩阵，W×Y和N×1是空间滞后向量，能够指出来自其他观测值的影响，γ是空间滞后的系数。X是一个带有解释变量M以及观测项N的N×M矩阵，β是解释变量的一个1×M的向量系数。μ是带有空间自相关的回归模型的残余项，ρ是μ的系数，∈是没有任何自相关的独立误差项[3]。

在方程（5）中，当ρ=0,γ×β≠0时，空间回归模型如下所示：

当γ=0，ρ×β≠0时，空间误差模型就变成如下所示：

然而，W1Y并不是模型的外生向量，所以应该采用Cliffde（1981）提出的最大似然估计模型（MLE）。

四、数据描述

截面数据库是由房地产服务公司世邦魏理仕公司提供的。该库包含了于2011年8月在上海的109家零售地产的信息。表1给出了有关的描述性统计数据。以前大多数的有关零售租金预计的研究将实际的租金作为自变量（Sirmans和Guidry，1992，等），然而数据库显示，更多的上海零售合同是以一种风险分摊的方式签署的。通过翻倍每月租户的总租金额来得到一个租金百分比，而事先会在租金合同中商定一个特定的百分比。上面提的租金百分比在表中以percentage～t表示的。为了使租金率的统计效应更好，会对以上提到的因变量百分比取对数，转化成：Y=ln(percentage～t)。

虚拟变量DGi指出了政府所指定的零售地产的特定位置。然而上海的零售市场格局并不是按照政府规划的那样划分出来的，所以虚拟变量D1和D6用来指代不同方位的商务地产，这些商务地产对应于零售业的地产等级（Wang el al.2006;Jackson，，2000）。地产等级在零售业高速发展的地区更高些。通过Wang et al.（2006）的调查问卷显示，上海的零售市场呈现出两极格局：在静安CBD地区以及黄浦江以西的外滩地区的商店每平米销售额要高于这两极之间的商店每平米销售额。其他的零售地产也遵循这种模式，所以用来指代地区位置的变量也遵循这种模式。

在图2中，由政府规划的区域都已命名，如闵行，卢湾等等。从D1到D4的新开发区域由圆1到圆4表示，D5区域由数字5表示，图中的其他区域由D6表示。租金的水平同样根据零售的不同类型而有所差别：商业区中心区以及百货公司的租金要高于贸易市场以及经销店的租金。购物中心和百货广场通常位于东方大都市（如香港和上海）的商业区，并且城市中心每平米的价格是最高的。一流的商户通常都选择在百货公司或购物中心租入，所以可以在这些地方找到比较高的零售租金价格水平。

表1描述性数据

图2 上海市中心区域规划

变量租用年限表明零售地产的最迟翻修以及重新开张时间。有一些论文（Sirmans和Guidry，1992）认为零售地产的租用年限和租金水平呈负相关，因为新的零售地产通常在建筑设计和构造方面优于老建筑。但是，老零售地产或许在顾客认可度和忠诚度方面有优势，并且新开张的零售地产或许会降低他们的租金以寻求固定的租户[4]。本文会检验这两个假设。变量TotalA和Retail A分别代表了整个建筑物的面积以及建筑中零售部分的总面积。更大的零售物业有望吸引更大的客流量，因为大零售地产能够提供更多的功能和服务内容以满足顾客各种各样的需求。由于参数之间具有弹性关系，总面积和零售面积变量可以转化为它们的估计参数的自然对数形式。为了更好地控制空间的相关性，变量dtocbd和dtobunds 6作为独立变量产生[5]，并用来预测到静安CBD以及Bund 6购物中心的距离。上面提到的这两个区域在上海的租金水平是最高的，这两个独立变量与租金水平呈负相关。用方差膨胀因子（VIF）来检测多重共线性。来自OLS回归模型的结果如表3显示。

五、结果分析

某些变量之间呈高度相关性（如表2所示），所以应该使

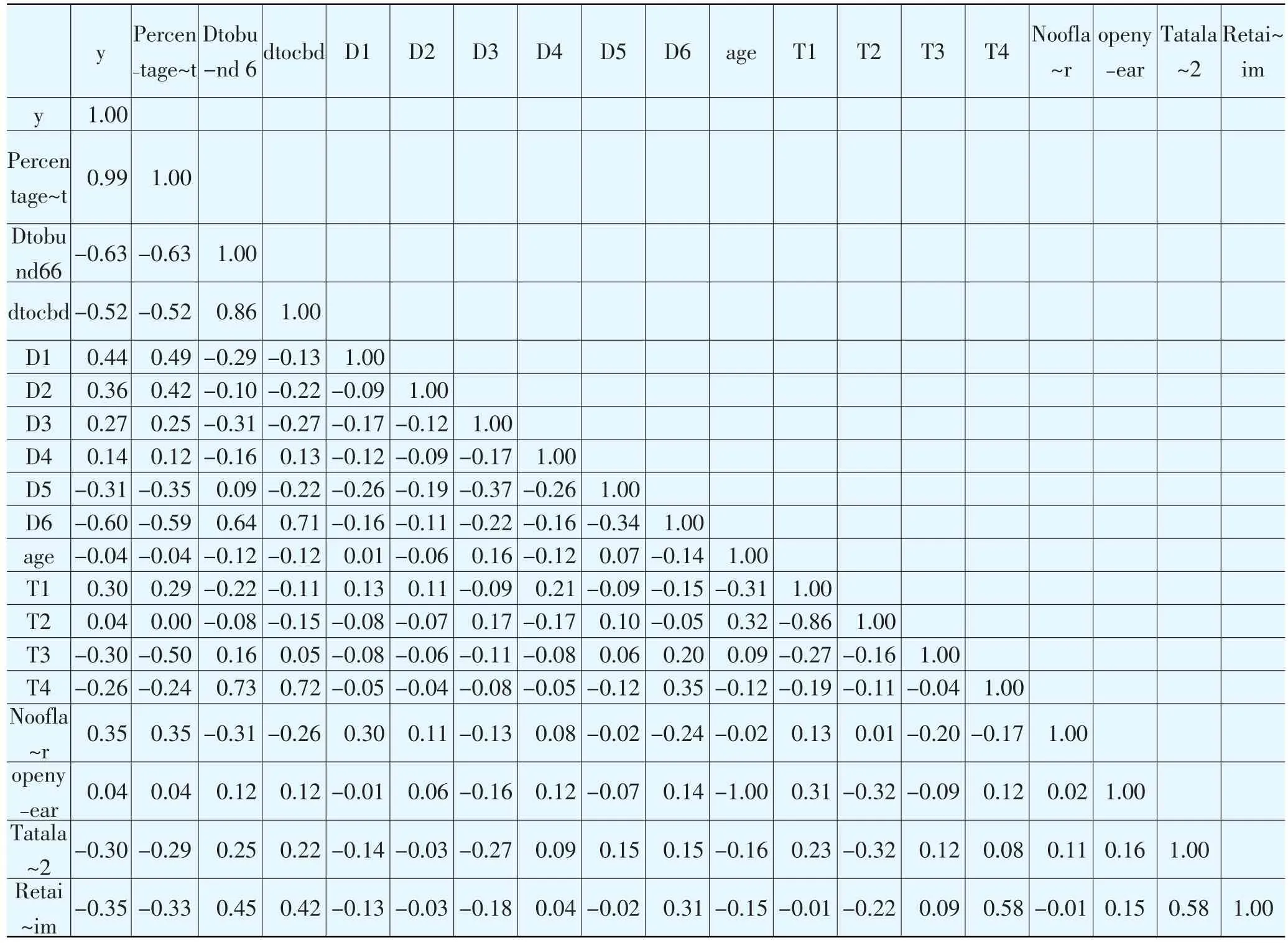
表2 变量相关性关系

模型（2）中的Breusch-Pagan test的F值是5.27，说明模型（2）存在异方差性问题，并且已经干扰到了估计，应该使用有修正程序的估计。在修正后，三个模型的F测试的结果很高（分别为7.92，206.05，28.83），足以证明解释变量结果都是显著的。

在第一个模型中，约74%是由因变量的变化解释的。平均的VIF值是9.1（VIF测试结果可以从表4、表5、表6中找到），不存在显著的多重共线性的问题。变量DGi的解释效力是不显著的，所以可以定义更好的分类方法。第二个模型中使用了新的区域变量Di，大约92%的自变量的波动是能够得到解释的。第二个模型的平均VIF值是8.43，不存在显著的多重共线性问题。

租用年限的边际效应预计是负效应（-0.01）并且非常显著。在第二个模型中，零售的不同类型也认为是很重要的。如果所有其他条件相同的话，那么在购物中心和百货公司的租金水平是最高的。而到静安CBD的距离、到外滩的距离、层数、总面积以及租赁面积这些因素的解释效力实际是不显著的。在第二个模型中，变量Di在解释租金方面是非常显著的，拥有最高租金水平的区域用D2（静安CBD区域）来表示。最低租金水平的区域是D6，该区域的租金水平比D1要低65.38%，在零售研究的大背景下，变量Di比DGi的解释能力要强，因为它们的解释能力都是得到过改进的，而且所有的Di都是非常重要的。

在第三个模型中，集成变量也纳入了回归的范围，尽管所有的独立变量是不重要的，第三个模型的结论的解释效力仍然是最高的（调整后的R2是0.9117）。模型的VIF值是18429，所以就存在多重共线性的问题（Rosiers和Riault，2001）。在这个案例中，变量的估计值的方差可能会非常高，模型中变量的系数会变得非常不可靠（O'Brien et al，2007）。但是，这个模型可以用来预测，并且当样本容量增加时，这个估计就会得到改进。

六、空间自相关性政策以及空间回归模型

空间自相关测试显示，当测试中使用了平方反比的距离矩阵时，Z分数的统计值分别增加到1.65，1.54以及1.53。空间自相关效应非常接近于显著水平。在这个案例中，空间滞后模型以及空间误差模型用来捕捉空间的依赖程度。空间滞后模型和空间误差模型在第二个模型回归时使用了同样的变量。第一个和第三个模型没有被使用的原因是第一个模型在检测租金的方差方面效力不足，而多重共线性问题严重干扰着第三个模型。括号内的T-值，正如表7显示，在OLS模型中，零售面积的变动有一个正系数，而在空间回归模型中，这种变动是负的。

除此以外，空间回归模型和OLS模型之间的预测差异是非常小的。

表3 OLS回归估计的结果

表4 VIF-test结果模型

表5 VIF-test结果模型

表6 VIF-test结果模型

表7 决定零售业租金因素的空间回归模型

为了找出能在实际中应用的最好的估计，需要执行平均平方根误差测试（RMSE）：在总共85个观测值中，随机选出75个观测值来估计新的系数，所以新的估计模型就用来预测剩下的十个观测残差。拥有最小平均偏差的模型将会被选取。测试结果在表8中显示出来，并且最后选出了拥有最小偏差的空间滞后模型。

表8 RMSE测试结果

七、研究结论

在零售研究的大背景下，本文采用了一个在区域分类的新方法，在解释不同类型地产零售租金变动方面，该方法要比政府所规划的区域要更为有效。当使用OLS模型时，空间自相关被证明是比较重要的一个问题。空间滞后模型和空间误差模型用来预测影响零售租金的决定因素，得出的结果可以和OLS模型进行比较。为了找出最适合的模型以在实践中进行预测，需要进行平均平方根误差测试（RMSE），并且空间滞后模型被认为是用来预测的最佳模型。通过选取85个观测值代入回归模型的实证研究，得出了上海地区零售租金的决定因素。在模型中得出的重要解释变量有地产的租用年限（负相关）、零售地产的类型、以及地产所处的区域。而层数、建筑物总面积以及租赁面积并不是重要的解释变量。这个结论为研究上海的零售地产租赁提供了重要的依据，也为实务中的上海投资决策提供了重要参考[6]。在这个结论的基础上，后续的研究就可以把重点放在地产的租用年限、零售地产的类型、地产所处的区域上面，为上海零售商务地产的投资和开发提供指导。本文结果还显示，最高的零售地产价格份额是在D1（南京东路）和D2（静安CBD），购物中心以及百货公司比贸易市场以及经销店拥有更高的租金水平。

[1]Roura Juan R.Cuadrado&Alvaro Ortiz V.Abarca.Business Cycle&Service Industries：General Trends&the Spanish Case[J].The Service Industries Journal，2001，21：103-122.

[2]Filardo，Rew J.Cyclical Implications of the Declining Manu⁃facturing Employment Share[J].Economic Review-Federal Reserve Bank of Kansas City，1997，82：63-87.

[3]Wyck off，Andrew.The Growing Strength of Service[J].OECD Observer，1996，200：11-15.

[4]Julius，De Anne，John Bulter.Inflation&Growthi-naService Economy[J].Bank of England，1998，38：338-346.

[5]Gene M.Grossman and Elhanan Helpman.Innovation and Growth in the Global Economy[M].Cambridge：MIT Press，1991.

[6]张亚斌，易红星，林金开.进口贸易与经济增长的实证分析[J].财经理论与实践，2002，（11）：32-43.