分数阶Fourier变换与新型时频滤波器设计

闫 格，刘开华，罗 蓬，吕西午

（天津大学电子信息工程学院，300072 天津）

分数阶Fourier变换与新型时频滤波器设计

闫 格，刘开华，罗 蓬，吕西午

（天津大学电子信息工程学院，300072 天津）

为了无失真地恢复复杂噪声环境中的非平稳信号，提出一种新型分数阶Fourier变换时频滤波器设计方法.该方法先利用Gabor变换得到信号在时频域的分布状况，然后用支撑向量机(SVM)分类算法结合图像分割得到分离时频图像上信号和噪声区域所需的最优分类线，最后用此最优分类线方程确定时频滤波器的阶数和传递函数.在信号和噪声时频域线性不可分的情况下，对SVM分类曲线进行了全局最小二乘分段线性拟合，然后根据拟合生成的方程构造并行多阶滤波器组.为满足实际应用中实时性的要求，对算法的计算复杂度进行了优化.计算机仿真结果验证了该方法的有效性.

时频滤波;Gabor变换;图像分割;支持向量机;分数阶Fourier变换

现今非平稳信号处理是现代信号处理领域一个重要分支，尤其是非平稳信号的滤波技术，一直是学术界研究的热点.由于非平稳信号的频率分布具有时变特性，因此无法单独在时域或频域上对信号进行滤波处理.近年来，随着时频分析理论的蓬勃发展［1－3］，尤其是离散分数阶 Fourier变换(fractional Fourier transform，FrFT)在数字信号处理中的应用，使得新型时频滤波器设计有了新的解决方案.FrFT作为Fourier变换的广义形式，可以描述为时频平面的旋转算子［4］在统一的时频域上对信号进行分析.利用该特点，时频滤波器的设计［5－6］中可以采用FrFT技术实现对非平稳信号的参数检测和估计及某些形式的干扰和噪声的消除.在文献［7］和［8］中，提出了基于最小均方误差准则的分数阶Fourier域最优滤波算法.在文献［9］中，给出了分数阶Wiener滤波算子的离散化求解算法.然而，这些算法是现代滤波器设计理论在分数阶Fourier域上的延伸和推广，在设计时需要信号和噪声的统计先验知识，并且只局限于单个旋转角度上的滤波.在文献［10］中，利用Fr-FT的旋转可加性，实现了多个阶次上的迭代滤波.但该方法运算复杂且无法保证迭代过程收敛到全局最优解.文献［11］中，利用时频变换先确定时频滤波器阶次和传递函数，然后将分数阶Fourier域滤波器等效于时频面上的一条分类线.此方法为时频滤波器设计提供了良好的思路，但在文献中没有提出具体的设计方法和合理的分类线选择依据.

本文提出了一种新型FrFT时频滤波器设计方法.该方法根据信号和噪声的时频分布采用Gabor变换(Gabor transform，GT)、图像分割、支持向量机(support vector machine，SVM)等技术，自动地获取区域间的分类线，然后根据分类线方程确定时频滤波器的参数.该方法设计过程无需任何信号和噪声的统计先验知识，且能够保证滤波器的最优性能.在信号和噪声的形式、强度、分布均未知的情况下，该方法依然适用，具有良好的可靠性和通用性.

1 分数阶Fourier域滤波器原理

对任意信号s(t)，旋转角度为α的FrFT定义为［4］

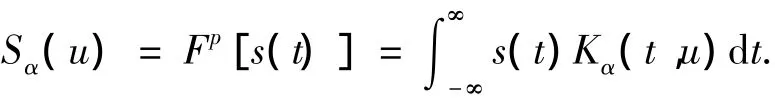
式中:定义 FrFT 的阶为 p;α =pπ/2，Kα(t，u)为变换的核函数，则有

一般称u域为分数阶Fourier变换域，其中α=0与α=π/2分别表示信号的时域和频域.FrFT可以被描述为时频面上的旋转算子，即1个信号的FrFT的Wigner分布(Wigner distribution，WD)是原信号Wigner分布的坐标旋转形式，用公式表示为

式中WD定义为

考虑一组含有加性噪声的非平稳信号x(t)=s(t)+n(t).其中s(t)和n(t)分别表示有用的非平稳信号和加性噪声，假设其时频分布如图1所示.可以看到有用信号和噪声在时域和频域同时存在耦合但不交叠，即无法单独通过时域或频域滤波完全滤除噪声，但由于两者的封闭性可通过切割分离.

图1 分数阶Fourier域上的噪声分离

利用FrFT将坐标轴旋转到合适的角度，构造分数阶Fourier域滤波器即可实现噪声的完全滤除和信号的无失真恢复.该滤波器可以表示为

式中r(t)为恢复信号，H(u)为时频滤波器传递函数.可将式(1)所示的时频滤波器等效于时频面上的一条分类线，有用信号和噪声的分布区域可以通过该分类线完全分离.时频滤波器的变换阶次p可以由所得分类线的斜率k确定，即p=－2arccot k/π，而滤波器的截止频率u0等于原点到分类线的距离.

对于更加一般的信号分布，需要将时频平面多次旋转才能逐步消除信号和噪声的耦合.此时可将单阶时频滤波器扩展为连续变化阶次的时频滤波器组，即

显然，分数阶Fourier域滤波器的设计重点是有用信号和噪声区域间的时频分类线的确定方法.通过图1可以看出，能够将两个区域完全分离的直线不具备唯一性.因此，如何制定约束条件，并根据信号和噪声的分布，寻找一条最优的分类线将成为分类线确定方法的关键.

2 时频滤波器设计方法

2.1 时频图像的获取及分割

为了在时频面上准确定位各信号和噪声分量，需要对观测信号进行时频变换.本文通过计算信号的Gabor变换获取信号和噪声的时频分布，即

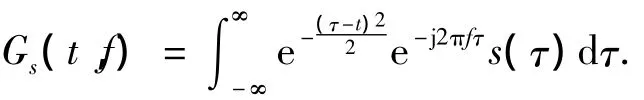
由于GT是一种线性变换，不受交叉项干扰，对于观测信号x(t)=s(t)+n(t)，有

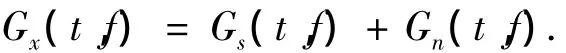
通过Gabor变换，可以得到一幅观测信号的时频图像，该图像由信号区域、噪声区域以及背景区域三部分组成，且各像素点的像素值对应于该时频点的Gabor系数.这里假设各信号和噪声分量的分布区域没有重叠.

为了实现不同区域的分离，特别是有用信号和噪声区域的分离，本文采用区域生长图像分割技术［12］对Gabor图像进行处理.该方法能够获得良好的边界信息和分割结果，对于各信号分量的强度和分布边缘差异较大的情况依然适用.最后，对所得的各时频区域附加不同的区域标识，即可实现各区域的分离.

2.2 最优时频分类线的确定

SVM是一种通用机器学习方法，在信号分类和识别等领域有着广泛的应用.本文利用SVM的学习机制获取信号和噪声区域间的唯一分类线，并根据分类线方程设置合理的时频滤波器参数.考虑如下形式的点的集合:

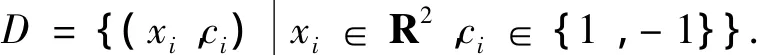
其中:i=1，2，…，N.xi为二维位置向量，代表Gabor变换生成的时频图像中的1个像素;ci为xi的类别标识，取值区间为1或－1，取1表示该向量属于信号区域，取－1则表示信号属于噪声区域.将集合D所包含的点作为SVM分类器的训练集，优化目标是寻找一条区分两个区域的最优分类线.此分类线的设计准则是不但能将所有向量xi正确分类，而且使得分类间隔最大.分类线定义如下:

上式中，定义w为系数向量.为使对于训练集D，满足如下正确分类条件:

对式(3)进行归一化，可得归一化分类间隔为Mmargin=2/‖w‖.

综合以上可定义SVM最优分类线为满足条件(4)且使得分类间隔最大的分类线.有用信号区域和噪声区域中距离分类线最近的向量称为支持向量.上述问题可以通过二次规划理论寻求最优解，本文采用文献［13］提出的优化算法对分类线参数进行求解.

2.3 时频区域线性不可分情况

对于线性可分情况，可以直接根据SVM分类线方程确定时频滤波器各项参数，然后利用式(1)即可进行噪声的滤除以及有用信号的恢复.

对于线性不可分情况，通过合理选取SVM核函数，可以得到一条曲线形式的最优分类线.该分类线无法直接用于滤波器参数选择.在这种情况下，为方便滤波器设计，本文提出在全局最小二乘误差准则下，对非线性SVM分类线进行分段线性拟合，形成一组首尾相接的线段，进而根据各线段的参数分别设计相应的多阶时频滤波器组.已知非线性分类线上的M个数据点

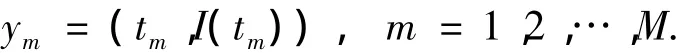
式中f=I(t)为曲线分类线方程.对于数据组ym，求解满足最小二乘误差准则

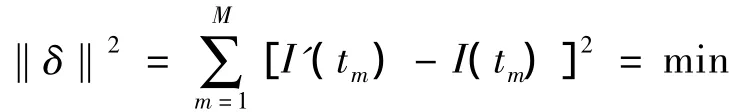
的分段线性拟合折线方程f=I'(t)的方法即最小二乘拟合.所生成的分段线性拟合折线方程表示为

点(tn，fn)，(n=1，2，…，N+1)为时频面内分段线性拟合折线段的起点和拐点.N为分段数，选择合适的N值，保证完全分离有用信号和噪声.然后根据每段的拟合方程确定相应阶的时频滤波器组的参数，进而利用式(2)逐次滤波即可实现噪声的完全滤除.

实际应用中，采用并行时频滤波器组实现方式更为高效.首先根据拟合的曲线分类线，将观测信号在时域分成N段，每段信号对应于拟合折线段中的一段，即

根据拟合结果确定各子滤波器的参数，并对对应的观测信号段进行滤波处理，将所有输出信号叠加，作为最终的恢复信号，即

上述并行结构相比于式(2)所示的串行滤波器组具有明显的优势.首先，每段观测信号仅进行一次FrFT正逆变换，避免了多次FrFT所引入离散化误差.其次，各段信号的分段滤波过程可以设计并行硬件单元结构实现，提高了计算速度.由此可见并行时频滤波器组结构拥有精度和计算速度两方面优势.

2.4 算法流程及细节

算法的流程如图2所示.

图2 算法流程

在实际应用中，需要计算离散分数阶Fourier变换.本文选用Pei Soo-Chang等［14］提出的采样型快速算法.该算法满足FrFT的周期性、可逆性以及分数阶Fourier域采样定理［15］，并且可以较为准确的逼近连续FrFT的结果.这种快速算法利用工程中常用的FFT来实现.算法的计算复杂度为O(Nlg N).

本文所提出的时频滤波器设计方法的前提假设是:信号和噪声的时频分布有耦合但无交叠.因而该方法对信号和噪声的先验性要求较低，在雷达等应用领域，感兴趣信号多为非合作信号，干扰信号形式复杂且随机性强，没有先验知识可以利用，此时利用该方法可以获得良好的滤波效果.然而对于信号畸变及信噪无法分离的情况，则需要引入一定的现代滤波方法实现信号的有效恢复.

2.5 减少算法复杂度的措施

工程应用中，需要对接收信号高速、实时地进行滤波处理.在本文所提设计方法中的SVM分类算法占据了大部分的运算量.为了降低运算量，可采用下述措施进行优化:

1)Gabor-Wigner变换.Gabor变换的分辨率低，在时频图像上表现为信号和噪声区域占据的面积增大.而有效像素点的增加必然导致SVM训练集的扩大.SVM分类器的运算量又取决于训练集数据的个数.因此时频图像的分辨率是影响算法复杂度的重要因素.文献［11］提出了 Gabor-Wigner变换(GWT)的定义如下:

式中:Gs(t，f)和Ws(t，f)分别表示信号的 Gabor变换和Wigner分布;h(x，y)表示任意二元函数.合理的选取h(x，y)的形式，可以使GWT在避免交叉项干扰的同时保持和Wigner分布具有相同的高分辨率.综合以上特点，通过GWT获取信号的时频图像表示，可以有效减小SVM训练集的规模，达到降低运算复杂度的目的.

2)图像边缘提取技术.根据SVM的原理，只有支持向量对训练结果产生影响，因此支持向量可以唯一地确定分类线的方程.由于本文假设信号和噪声在时频面上的分布均为连通闭合区域，所以所需的支持向量必然位于两区域的边缘.由此可以推出，采用图像边缘提取技术［12］，由各区域的边缘像素组成训练集，可以有效降低SVM分类器的训练复杂度.

3 仿真实验

3.1 实验一

本实验为信号和噪声线性可分情况.假设信号和噪声均为高斯调幅的线性调频信号，表达式为

信号的观测区间为 －2 s到2 s，采样率为fs=100 Hz.观测信号x(t)=s(t)+n(t)的Gabor时频分布如图3所示.由图3可以看出，耦合同时存在于信号和噪声的时域和频域.

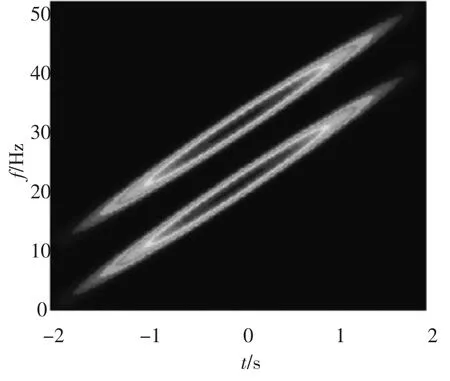
图3 观测信号的Gabor变换

如图4所示，对Gabor变换后的图像进行区域分割，利用不同区域内像素构成的训练集，训练SVM分类线.

图4中，SVM训练得到的最优分类线方程为

然后利用分类线的参数确定时频滤波器的阶数及传递函数对观测信号进行滤波，所得到恢复信号的时域波形和恢复残差如图5所示.

图4 线性SVM分类线及支持向量

图5 恢复信号及恢复残差

根据实验结果，时频滤波器的信噪比改善因子由式(5)计算得FIF=29.049 5 dB，信号恢复均方误差由式(6)计算得EMSE=0.124 46%.

在上述实验的基础上，构造4条典型非最优分类线，用于考察SVM分类线的最优特性对滤波器性能的影响.如图6所示，4条分类线同样可以达到将两个区域完全分离的效果，直线分类线方程分别为

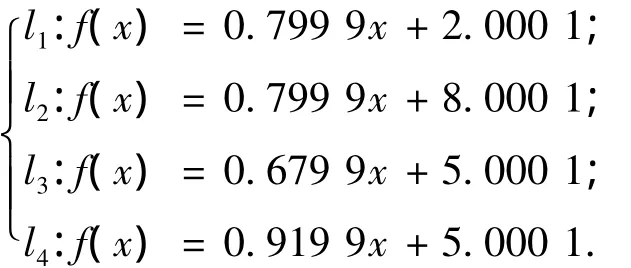
图6 典型非最优分类线

分别对上述4条分类线构造对应的时频滤波器，并用其对观测信号进行滤波处理，滤波性能统计结果如表1所示.

表1 4条典型分类线对应的滤波结果

由上述结果可以看出，本文方法在信号和噪声分布线性可分的情况下，可以实现噪声的有效的滤除.同其它时频分类线的滤波效果对比可以看出，SVM分类线设计的时频滤波器具有最优的性能.由于SVM以最大化分类间隔作为优化目标，克服了观测信号的时域截断以及离散谱分析的栅栏效应造成信号和噪声的能量向整个时频平面泄露，在时频面上表现为可以最大程度地分离信号和噪声，从而提高滤波器的性能.

3.2 实验二

本实验为有用信号和噪声线性不可分情况.考虑线性不可分情况，信号和噪声方程如下:

信号观测时间段为－10 s到10 s，采样率为fs=30 Hz.信号的Gabor时频分布如图7所示.信号和噪声区域间的非线性SVM最优分类线如图8所示.

图7 信号的Gabor变换

对图8中的SVM分类曲线进行全局最小二乘分段线性拟合，拟合段数为N=4(拟合的段数等于滤波器的阶数)，其拟合结果如图9所示.

图9中，折线段的拟合方程组为

利用SVM折线段拟合的方程参数确定并行时频滤波器组的参数，并对输入信号进行4阶滤波，所得恢复信号的时域波形以及恢复残差如图10所示.

图8 非线性SVM分类线及样本支持向量

图9 SVM分类曲线的4段线性拟合

图10 恢复信号及恢复残差

根据图10所示实验结果，由式(5)～(6)分别计算时频滤波器的信噪比改善因子和信号恢复均方误差，其结果为:FIF=28.180 8 dB，EMSE=0.1520 3%.

由上述结果可以看出，本文方法在信号和噪声分布线性不可分的的情况下，仍可实现噪声的有效滤除.由于非线性分类线的拟合的误差和多阶滤波器组引入了额外的FrFT离散化误差的影响，同线性可分情况相比，此时频滤波器的性能略有下降.

4 结论

本文针对非平稳信号的波形恢复问题，提出了一种基于FrFT的新型时频滤波器设计方法.该方法属于经典滤波器在分数阶Fourier域上的扩展，设计过程无需信号和噪声的先验知识，简单直观且具有良好的信噪比改善性能，适合工程实现.仿真结果显示，在信号和噪声耦合但不交叠的前提下，该方法针对信号和噪声区域线性可分和线性不可分两种情况都能实现噪声的滤除和信号的无失真恢复.如何在该方法中融合现代滤波的相关思想，解决信号畸变以及信噪交叠难分离的问题，且进一步优化运算的复杂度，都是今后需要进一步研究的课题.

［1］MILLIOZ F，MARTIN N.Circularity of the STFT and spectral kurtosis for time-frequency segmentation in Gaussian environment［J］.IEEE Transactions on Signal Processing，2011，59(2):515 －524.

［2］LU W K，ZHANG Q.Deconvolutive short-time Fourier transform spectrogram［J］.IEEE Signal Processing Letters，2009，16(7):576 －579.

［3］XING M，WU R，LI Y，et al.New ISAR imaging algorithm based on modified Wigner-Ville distribution ［J］.IET Radar，Sonar and Navigation，2009，3(1):70 －80.

［4］ALMEIDA L B.The fractional Fourier transform and time-frequency representations［J］.IEEE Transactions on Signal Processing，1994，42(11):3084－3091.

［5］OZAKTAS H M，BARSHAN B，ONURAL L，et al.Filtering in fractional Fourier domains and their relation to chirp transforms［C］//Proceedings of the 7thMediterranean Electrotechnical Conference，Antalya.Antalya:［s.n.］，1994:77 －79.

［6］OZAKTAS H M，BARSHAN B，MENDLOVIC D.Convolution and filtering in fractional Fourier domains［J］.Optical Review，1994，1(1):15－16.

［7］ZALEVSKY Z，MENDLOVIC D.Fractional Wiener filter［J］.Applied Optics，1996，35(20):3930 －3936.

［8］KUTAY M A，OZAKTAS H M，ONURAL L，et al.Optimal filtering in fractional Fourier domains［J］.IEEE Transactions on Signal Processing，1997，45(5):1129－1143.

［9］齐林，陶然，周思永，等.LFM信号的一种最优滤波算法［J］.电子学报，2004，32(9):1464－1467.

［10］ERDEN M F，KUTAY M A，OZAKTAS H M.Repeated filtering in consecutive fractional Fourier domains and its application to signal restoration［J］.IEEE Transactions on Signal Processing，1999，47(5):1458 －1462.

［11］PEI S C，DING J J.Relations between Gabor transforms and fractional Fourier transforms and their applications for signal processing［J］.IEEE Transactions on Signal Processing，2007，55(10):4839－4850.

［12］GONZALEZ R C，WOODS R E.Digital image processing［M］.New York:Prentice Hall，2002.

［13］CHAPELLE O.Training a support vector machine in the primal［J］.Neural Computation，2007，19(5):1155－1178.

［14］PEI S C，DING J J.Closed-form discrete fractional and affine Fourier transforms［J］.IEEE Transaction on Signal Processing，2000，48(5):1338－1353.

［15］TAO R，DENG B，ZHANG W Q，et al.Sampling and sampling rate conversion of band limited signals in the fractional Fourier transform domain［J］.IEEE Transaction on Signal Processing，2008，56(1):158 －171.

Fractional Fourier transform and novel time-frequency filter design

YAN Ge，LIU Kai-hua，LUO Peng，LU Xi-wu

(School of Electronics and Information Engineering，Tianjin University，300072 Tianjin，China)

To realize the lossless recovery of non-stationary signal in complicated noise environment，a novel design method based on fractional Fourier transform of time-frequency filter is proposed，in which the time-frequency distribution of incident signal is obtained by Gabor transform first，and then based on support vector machine(SVM)and technique of image segmentation，the regions of signal and noise on the time-frequency plane are separated and the optimal separating line is drawn，finally the order number and transfer function of the time-frequency filter can be determined by the optimal separating line equation.For the case of linearly inseparable signal and noise time-frequency distribution，the piecewise linear fitting based on global least square criterion is performed to the separating curved line，and the parallel filter banks are constructed from the linear fitting equation.To meet the real-time requirement in engineering application，the computational complexity was optimized，and the simulation results demonstrated the validity of this method.

time-frequency filtering;Gabor transform;image segmentation;support vector machine;fractional Fourier transform

TN911.72

A

0367－6234(2012)09－0138－06

2011－08－06.

天津市科技支撑计划资助项目(10ZCKFGX03600).

闫 格(1983—)，男，博士研究生;

刘开华(1956—)，男，教授，博士生导师.

闫格，eye_ge@163.com.

(编辑 张 宏)