活用动能定理巧解题

蓝春杰

（青岛市城阳区第一高级中学，山东 青岛 266108）

动能定理是高中学习中常用的比较重要的定理之一.在应用其处理物理问题时，不涉及具体的运动过程，给解题带来了很大的便利；在求解不涉及时间的问题时也用动能定理来处理.动能定理除用来处理常规的题目，在处理有些疑难问题时，往往具有独辟巧径、轻盈灵动的特点.

1 活用动能定理巧求变力功

例1.用汽车从井下提重物，重物质量为m定滑轮高为H，如图1所示，已知汽车由A点从静止开始运动到B点时的速度为vB，此时轻绳与竖直方向夹角为θ.这一过程中轻绳的拉力做功多大？

解析：绳对重物的拉力为变力，应用动能定理列方程.以重物为研究对象：

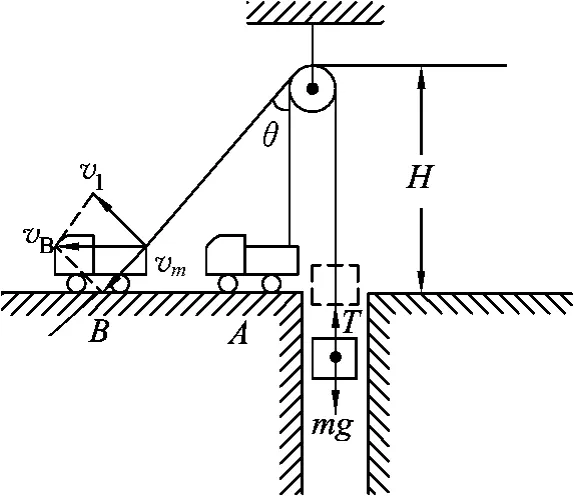
图1

由图1所示，重物的末速度vm与汽车在B点的速度vB的沿绳方向的分速度相同，则

联立（1）～（3）式解得

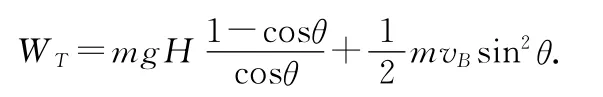
点评：如果所研究的问题中有多个力做功，其中只有一个力是变力，其余的都是恒力，而且这些恒力所做的功比较容易计算，研究对象本身的动能增量也容易计算时，巧用动能定理就可以灵活求出这个变力所做的功.

用动能定理解决变力做功的方法：一般不直接求功，而是分析动能变化再由动能定理求功.

2 活用动能定理巧求多过程问题

例2.如图2所示，在一个固定盒子里有一个质量为m的滑块，它与盒子底面间动摩擦因数为μ，开始滑块在盒子中央以足够大的初速度v0向右运动，与盒子两壁碰撞若干次后速度减为0，若盒子长为L，滑块与盒壁碰撞没有能量损失，求整个过程中物体与两壁碰撞的次数.

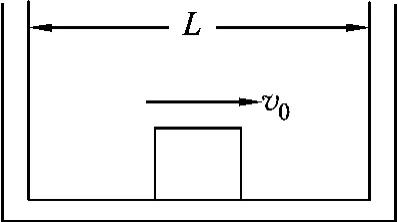
图2

解析：以滑块为研究对象，滑块在整个运动过程中克服摩擦阻力做功消耗了滑块的初始动能，依动能定理列方程，设碰撞n次，有

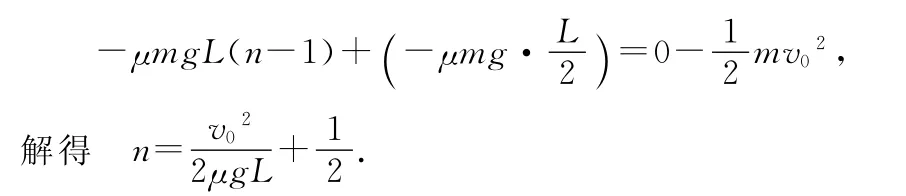
点评：滑块与盒子两壁多次作用，往复在盒子底部滑动，把动能消耗掉.该过程摩擦力的方向变来变去，但不管怎么变，摩擦力总是做负功.此题要注意摩擦力做功的大小是摩擦力乘以物体通过的路程而不是位移.

例3.质量m＝1.5kg的物块（可视为质点）在水平恒力F作用下，从水平面上A点由静止开始运动，运动一段距离撤去该力，物块继续滑行t＝2.0s停在B点，已知A、B两点间的距离s＝5.0m，物块与水平面间的动摩擦因数μ＝0.20，求恒力F多大？（g＝10m／s2）

解析：设撤去力F前、后物块的位移分别为s1、s2.物块受到的滑动摩擦力f＝μmg＝0.2×1.5×10N＝3N，撤去力F后物块的加速度大小为m／s2，最后2s内，物体的位移为2.02m＝4.0m.故力F 作用的位移s1＝s－s2＝（5.0－4.0）m＝1.0m.

对物块运动的全过程应用动能定理：Fs1－fs＝0，得

点评：本题应用牛顿第二定律也可求解，但比较烦琐，应用动能定理求解则简洁得多.求解时一定要注意，两个力作用的位移是不同的.

3 活用动能定理巧求多物体系问题

例4.如图3所示，在水平桌面的边角处有一轻质光滑的定滑轮K，一条不可伸长的轻绳绕过K分别与物块A、B相连，A、B 的质量分别 为mA、mB.开始时系统处于静止状态.现用一水平恒力F拉物块A，使物块B上升.已知当B上升距离为h时，B的速度为v.求此过程中物块A克服摩擦力所做的功.（重力加速度为g）

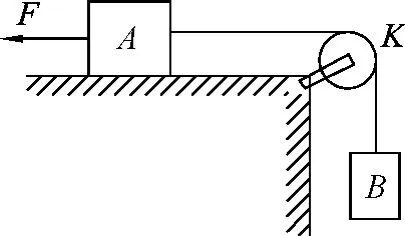
图3

解析：在此过程中，B的重力做功为mBgh，A、B动能增量为，恒力F所做的功为Fh，用W 表示A克服摩擦力所做的功，根据动能定理有

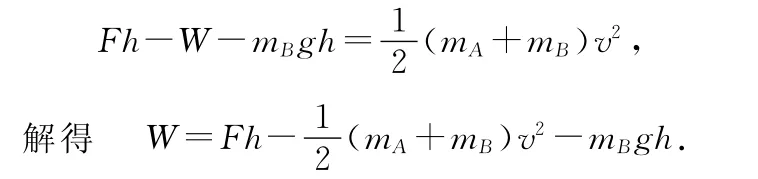
点评：对于多物体的问题，过程繁琐，用牛顿运动定律解题相对复杂，而用能量解题往往可以简化，但注意从能量角度如果对一个物体列方程是用动能定理，对系统往往是总体能量观点处理问题，也可以用动能定理.

4 活用动能定理巧求物体加速度

例5.如图4所示，两个物体的质量分别为m1、m2，m1＞m2／2.滑轮和细线的质量不计，细线不可伸长，不计滑轮转轴处的摩擦.开始用手托着m1，求放手后两个物体的加速度分别是多大？

解析：把m1、m2作为一个系统，设m1下降h时，则m2上升h／2，m1的下落速度为v，m2的上升速度为v／2，应用动能定理得

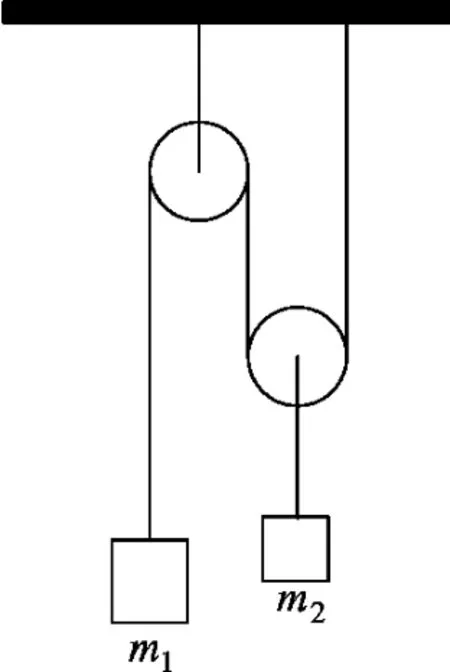
图4

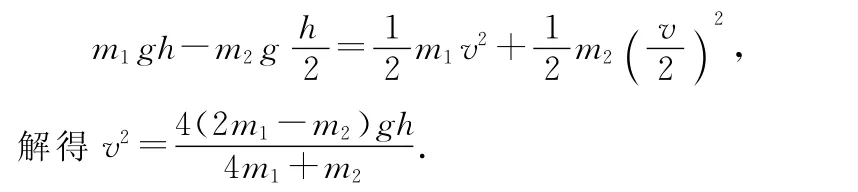
因m1匀加速下落，由v2＝2ah，得m1下落的加速度为

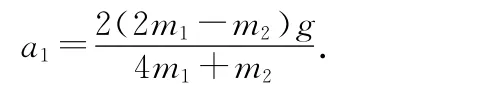
m2上升的加速度为

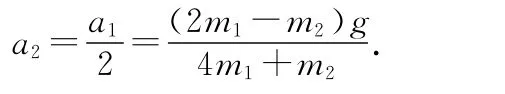
点评：用动能定理求物体加速度方法的实质是，把求物体加速度的问题利用动能定理转化为求速度和位移的关系式.这种方法对于多个物体组成的，多个物体间具有相互作用，且各个物体均做直线运动的一些较复杂的系统时，显得十分简单.