一种新型指数混沌系统及其DSP数字化实现

卢 军，王光义

(杭州电子科技大学电子信息学院，浙江杭州310018)

0 引言

在传统CDMA DS/SS通信系统中，采用伪噪声(Pseudo-Noise，PN)序列作为扩频序列。PN序列有理想的自相关特性，但相关函数呈现周期性。它们的互相关特性，特别是当部分相关时，有较大的尖峰。而且，相关特性比较好的PN序列的数目极为有限，一定程度上限制了现代移动通信的发展。而具有不同初始值的数字混沌序列数目众多，且互不相关，能够满足扩频多址通信中对扩频序列的要求，同时数字混沌序列容易产生，不需要存储各个序列点的值［1－3］。基于以上优点，本文提出了一个新的三维指数混沌系统，其具有3个混沌参数，一个乘积非线性项和一个指数非线性项，分析了该系统的基本动力学特性，包括对称性，耗散性以及稳定性等，并对系统进行了Matlab仿真，给出了相应的Matlab仿真实验结果，最后利用DSP处理器实现了这个三维指数混沌系统，并且将由混沌系统生成的数字混沌序列进行了NIST测试，测试结果表明序列随机性能良好。

1 新的混沌系统的提出

本文的系统是把Chen系统第三个方程中的xy乘积项换成了一个非线性的指数项exy。其动力学方程为:

式中，(x，y，z)∈R3，选取参数 a=35，b=3，c=28，初值为(0.1，0.1，0.1)时，系统有混沌解，从而系统处于混沌状态。混沌吸引子图及其在相平面上的投影如图1－4所示。

1.1 系统参数的影响

随着系统参数的改变，系统平衡点的稳定性将会发生变化，从而系统也将处于不同的状态。系统的分岔图和Lyapunov指数图都可以比较直观地反映非线性动力系统随参数变化的动态特性。固定参数b=3，c=28，改变 a，系统的 Lyapunov指数图和分岔图［4］分别如图5、6 所示:

图1 混沌吸引子图

图2 x-z平面吸引子图

图3 y-z平面吸引子图

图4 x-y平面吸引子图

图5 李雅普诺夫指数图

图6 分叉图

2 混沌数字信号的产生

首先，为了获得数字形式的混沌离散序列，得先将混沌系统离散化。由定义公式:

可得:

所以本文的连续系统可以表示为:

当离散系统中的 足够小时，离散系统和其对应的连续系统具有相同的动力学特性。在本文中，取0.000 5［3］。

由于DSP处理器运算速度快、可靠性好、可编程能力强和易于实现浮点运算等优点，本文采用DSP作为核心处理器，并结合软件CCS来生成混沌序列［2］。DSP实现的流程如图7所示:

图7 基于DSP产生混沌数字序列流程图

利用示波器观察到的数字序列如图8所示;通过数模转换得到的混沌吸引子分别如图9－11所示。由此观察可知，得到的混沌吸引子与前述所示的连续混沌的仿真结果一致。

图8 混沌数字序列

图9 y－z平面吸引子

图10 x－y平面吸引子

图11 x－z平面吸引子

3 混沌序列性能分析

美国国家标准技术研究院制定了一套关于序列随机特性测试的标准，从不同角度检验被测序列在统计特性上相对于理想随机序列的偏离程度。NIST测试结果如表1所示，以下为该测试软件包STS相关知识介绍。

表1 基于Chen系统的新型指数混沌系统NIST测试结果表

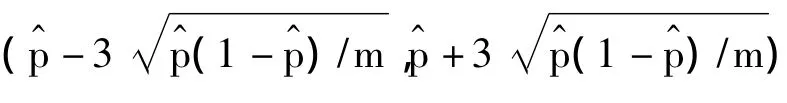
测试结果显示，在P-VALUE测试项中，数字混沌序列除了在Longest Run Test和Approximate Entropy Test的测试值为零，小于0.000 1外，其余项都满足要求;而在PROPORTION测试项中，数字混沌序列除了在Longest Run Test的测试结果落于可信区间外，其余项都满足要求;由此可得序列具有良好的随机性［3］。

4 结束语

本文在Chen系统基础上构造了一个新的三维指数混沌方程，利用Matlab数值仿真手段重点分析了系统参数对整个混沌系统的影响，并据此得出在系统参数的某一区间的新混沌系统状态。最后基于DSP实现了该指数混沌系统，与连续混沌的Matlab仿真结果一致，并对其生成的数字混沌序列进行了NIST测试，测试结果表明序列性能良好。

［1］ 周悦，朱灿焰，汪一鸣.混沌二进制序列性能分析［J］.苏州大学学报，2006，26(2):7－10.

［2］ 陈维，王光义.一个变参数变结构混沌系统及其数字化实现［J］.电路与系统学报，2011，16(6):99－103.

［3］ 王莹，王光义.混沌PN序列的DSP实现及其性能分析［J］.杭州电子科技大学学报，2012，32(1):1－5.

［4］ Donato Cafagna，Giuseppe Grassi.Bifurcation and Chaos in the Fractional Chua and Chen Systems with Very Low Order［C］.Salento:IEEE CONFERENCE PUBLICATIONS，2009:2 846 －2 849.

［5］ Gamal M，Mahmoud Emad E，Mahmoud Mansour E.On the hyperchaotic complex Lü system［J］.Nonlinear Dynamics，2009，24(8):725 －738.