基于MATLAB的直流调速数字控制系统的分析和设计
刘家鑫
(大连交通大学电气信息学院,辽宁 大连116028)
0 引 言
随着计算机技术的发展,直流调速系统的数字化控制已得到广泛应用。较之传统用模拟电路实现直流调速系统的触发和调节,数字调节器有着明显的优势。即用微机执行数字PID运算程序代替模拟转速调节器和电流调节器,而转速给定、转速反馈和电流反馈经A/D转换器变成数字量送入微机(或单片机),微机的运算结果通过D/A转换器变成模拟量作为可控整流装置的触发控制电压。这种方式不但克服了电网电压波动对触发精度的影响,而且在一定程度上也减小了因器件老化、温度变化引起的运算误差。由于计算机具有高精度、高速度和编程灵活等优点,可以在系统中灵活的使用各种算法实现最优控制;并且对控制结果的观察更加明确,对控制结果的分析也可以在显示器上绘制曲线来表示[1]。
计算机控制系统的经典设计方法一般分为两种。一种是将连续域设计好的控制律D(s)利用不同的离散化方法变换为离散控制律D(z),这种方法称为“连续域—离散化设计”方法,其允许利用熟悉的各种连续域设计方法设计出令人满意的连续域控制器,然后将控制器离散化,离散化过程较为简单。另一种方法是在离散域先建立被控对象的离散模型G(z),然后直接在离散域进行控制器设计。
1 系统数学模型的建立
控制系统的结构如图1所示。

图1 控制系统结构图
直流电动机在额定励磁下的等效电路如图2所示,其中电枢回路总电阻R和电感L,包含电力电子变换内阻、电枢电阻和电感。
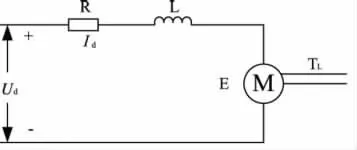
图2 直流电动机等效图
假设主电路电流连续,则电压方程为

忽略粘性摩擦及弹性转矩,电动机轴上的动力学方程为

额定励磁下的感应电动势和电磁转矩分别为

式中,TL为包括电动机空载转矩在内的负载转矩(N·m);GD2为电力拖动系统折算到电动机轴上的飞轮惯量(N·m2);Cm为额定励磁下电动机的转矩系数(N·m/A),Cm=Ce。
再定义下列时间常数:
Tl为电枢回路电磁时间常数(s),Tl=;T为m电力拖动系统极点时间常数(s),Tm=。
将上述参数代入式(1)和式(2),并结合式(3)和式(4)整理,并取拉普拉斯变换得到直流电动机的传递函数为

整流装置采用IGBT三相桥式整流电路,用PWM来控制。PWM控制的整流装置和晶闸管触发的动态数学模型基本一致,是一个滞后环节,其传递函数可以写成
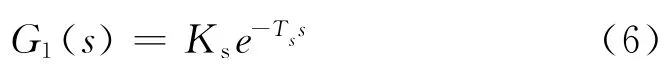
由于时间常数Ts非常小,所以对式(6)进行泰勒展开,近似等效成一个一阶惯性环节,即
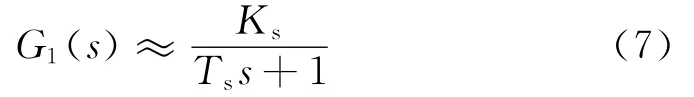
将转速反馈系数α折算到前向通道,给定值为原来的1/α倍,则直流调速系统的开环传递函数为

直流调速系统的实际参数具体如下:
转速反馈系数α=0.0158,机电时间常数Tm=0.075 s,电磁时间常数Tl=0.017 s,IGBT 开关频率为10 Hz,则Ts=0.1 ms。
将上述参数代入式(8)得

由于IGBT整流装置的时间常数Ts很小,可以忽略,则式(9)可以近似为
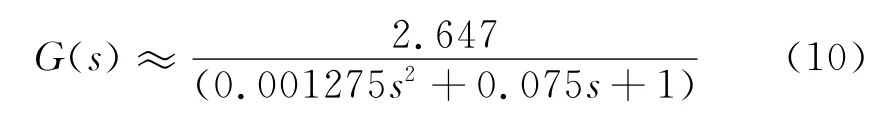
2 控制系统的设计和仿真
2.1 采样周期的选择
在计算机控制系统里,采样周期T是系统的一个重要参数,对闭环系统的稳定性和性能有很大的影响。一般地,采样周期越小,稳定性越好,但采样周期太小时,由于计算机运算部件、A/D和D/A变换器的字长有限,计算机控制系统并不趋于连续系统,且由于字长有限所产生的量化误差会增大。同时,采样周期过小时,将会增大控制算法对参数变化的灵敏度,使控制算法参数不能准确表示,从而使控制算法的特性变化较大。所以要考虑不同的因素,选取一个合适的采样周期。
为了减少频率混叠现象,选择采样频率时,常常要求采样频率满足
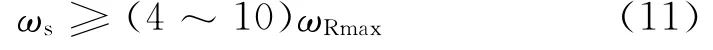
式中,ωRmax是被控对象全部特征根中的最高频率。本设计ωRmax=241.66(rad/s),所以Ts≤0.0026 s,取采样周期Ts=0.001 s。
2.2 数字PI控制器的设计
本文采用扩充临界比例度法来对PI控制器的参数进行整定。考虑零阶保持器的影响将被控对象离散化,再将数字控制器的积分与微分控制取消,逐步减小比例度σ(1/Kp),直到系统发生等幅振荡,得到临界比例度σk(1/Kk)和临界振荡周期Tk,然后查表得出各参数[2]。
对于临界比例度σk(1/Kk)和临界振荡周期Tk的获得,在此设计中采用根轨迹的分析方法,比直接测量阶跃响应更加方便和精确。
设计程序如下:


图3 只考虑比例环节的系统根轨迹
只考虑比例环节的系统根轨迹图如图3。运行结果为:用鼠标选取根轨迹与单位圆的交点即临界振荡点之后,得到 Kk=8.954,Wk=136.1434。则 Kk=8.954,Tk=0.1709 s。
控制度选1.05,通过查表1得Tl=0.0837 s,TD=0.0558 s,则 Kl=Kp/Tl=5.114,KD=KpTD=0.0239。
PID控制器D(s)=Kp+Kl经过双线性变换以后


表1 扩充临界比例度法选PID控制器参数

图4 数字PI控制系统的simulink仿真图
数字PI控制系统的simulink仿真如图4。从仿真结果看,系统无超调,稳态误差为零,效果较为理想。
然后求闭环极点,绘制波特图如图5对系统进行稳定性分析,程序如下:


图5 系统开环传函波特图

仿真结果为:

从图5看出,系统稳定,相角欲度Pm=105°,增益欲度Gm=43 dB。
2.3 Z平面根轨迹法
根轨迹法实质上是一种闭环极点的配置技术,通过反复的试凑,设计控制器的结构和参数,使整个闭环系统的主导极点配置在期望的位置上。在本设计中采用零极点对消法,即用控制器的零点对消被控对象的极点,使整个闭环系统具有满意的品质[4]。
设计指标为:超调量σ%≤20%;上升时间tr≤0.5 s;调节时间ts≤1 s;
(1)设计指标及期望极点的位置
典型二阶系统阶跃响应的动态指标为:

根据设计指标得出闭环阻尼比ζ≥0.456,z域同心圆半径r≤0.966,z域射线θ≥2.5°。
(2)数字控制器的设计
将被控对象考虑零阶保持器离散后,变成零极点形式,设计程序如下:

得到的零极点模型为:

则开环传递函数为:

结合动态指标,绘制系统的根轨迹程序如下:

系统的根轨迹如图6所示。
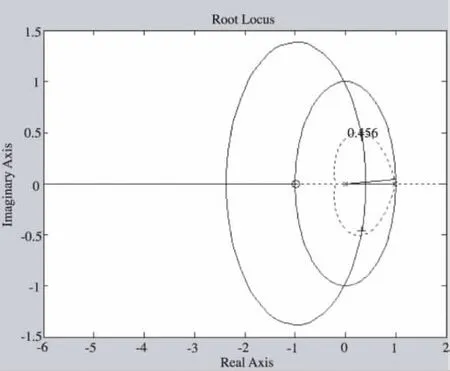
图6 考虑动态指标的系统根轨迹
在期望极点的区域内选取一对极点之后,运行结果为:

则K=0.3269,k=K/0.001=326.9

控制系统的Simulink模型图如图7所示,得到的阶跃响应曲线如图8所示[3]。
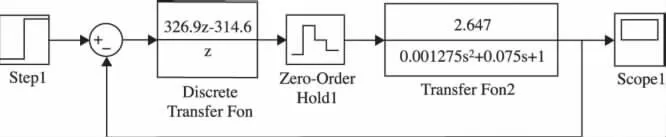
图6 控制系统SIMULINK的仿真图

图7 控制系统阶跃响应曲线
对系统进行动态响应分析,程序如下:

运行结果如图8所示。从图中可以看到闭环系统阶跃响应的超调σ%=15%,上升时间tr=0.00171 s,调节时间ts=0.00728 s,均满足设计指标。
求闭环极点,绘制波特图,进行稳定性分析,程序如下:
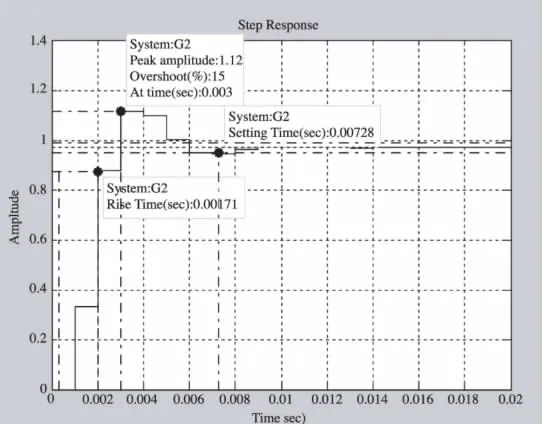
图8 显示动态指标的系统阶跃响应曲线

运行程序得到系统波特图如图9所示,闭环极点p=0.3264±0.4626 i。
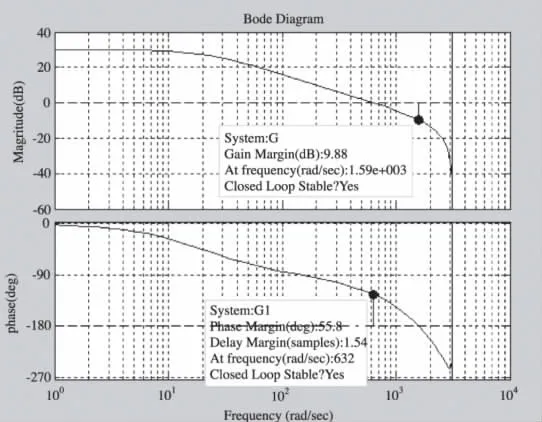
图9 控制系统开环传函波特图
从系统的闭环极点和开环传函的波特图中都可以看出,闭环系统稳定并且有足够的稳定欲度。
3 结 论
本文用了两种方法对直流调速系统的数字控制器进行设计。首先设计了数字PI控制器并采用扩充临界比例度法来对其参数进行整定。其中,利用临界振荡时根轨迹与单位圆相交的特性,更加精确地得出了振荡周期。另一种方法是Z域根轨迹法,对系统进行零极点的抵消和重新配置,设计出了满足性能指标的控制器。从这两种方法中均可以看出利用根轨迹来分析和设计一个控制系统的重要性。从根轨迹中不但可以直观地看到开环增益K对系统性能的影响,还能增加开环零极点来重新配置闭环主导极点,从而改变闭环系统的性能[5]。另外,从仿真分析中可以看出,MATLAB在对自动控制系统连续传递函数的离散化、系统的根轨迹、稳定性和动态响应过程的分析中起着非常方便和有效的作用。结合SIMULINK来建模分析,使得参数整定和系统调试更加方便和直观。
[1] 高金源.计算机控制系统[M].北京:清华大学出版社,2009.
[2] 陈伯时.电力拖动自动控制系统[M].北京:机械工业出版社,2003.
[3] 赵广元.MATLAB与控制系统仿真实践[M].北京:北京航空航天大学出版社.2009.
[4] 魏克新.MATLAB语言与自动控制系统设计[M].北京:机械工业出版社.2004.
[5] 高志宏.直流调速数字控制系统的仿真设计与参数优化[J].机电工程2008(8):49-51.

