矩阵变换器双空间矢量控制法的仿真研究

闫雪奎 ，郭 燚，王永康

（上海海事大学 物流工程学院 ，上海201306）

0 引 言

目前，通用的电压型交－直－交变频器应用较为广泛，但因其含有中间直流环节，直流部分的电感和电容导致其体积变大，并且谐波电流也对电网中其它用电设备产生了不利的影响。矩阵变换器很好地解决了上述问题，它不含中间直流环节，无大电感和电容，结构紧凑体积减小；输入侧电流谐波含量很少而接近正弦波，并且功率因数可调。矩阵变换器的诱人性能使其发展的前景变得广阔，对其进行研究也就具有十分重要的现实意义。

目前对矩阵变换器的研究方法主要有直接传递函数法、双空间矢量法、双电压法等多种调制方法，随着不同拓扑结构的出现，也将会出现更新颖有效的算法。

文献［1］中研究了基于直接传递函数法控制的原理，在MATLAB/Simulink平台上进行了仿真，并设计了相关的实验装置。但这种方法计算量太大，搭建的模型复杂，对于处理器要求较高，且最大的电压利用率只有50%。由文献［2］知，通过谐波注入法可以提高电压利用率。

文献［3］中对双电压法进行了仿真研究，这种方法也是一种直接计算的方法且计算相对简单。但不足之处是波形合成时可能出现不希望的某一相电压，从而对输出波形产生一定的影响，再者，相对于空间矢量脉宽调制的方法其控制算法的实现难度仍然较大。

文献［4］中指出，矩阵变换器在理论上可以等效为一个“虚拟整流器”和“虚拟逆变器”的串联电路模型，经典的空间矢量脉宽调制技术可以分别应用到这两个环节上，从而实现对矩阵变换器的调制。此方法计算简单易于实现，可以大大减小对控制电路的要求。

现在矩阵变换器的调制算法中，双空间矢量算法最为成熟，而基于该调制策略的矩阵变换器是交－交变换器研究中最具应用潜力的理想变换器。因此，本文在建立矩阵变换器的数学模型，双空间控制策略的数学模型等基础上，建立基于MATLAB/simulink仿真系统，进行有关的特性研究，为将来矩阵变换器的应用奠定一定的基础。

1 矩阵变换器的基本原理

基本的三相－三相矩阵式变换器是具有9个双向开关的交－交变换器，每个双向开关都具有双向导通和双向关断的能力，其电路拓扑结构如图1所示。a，b，c为三相输入端，A，B，C为三相输出端。

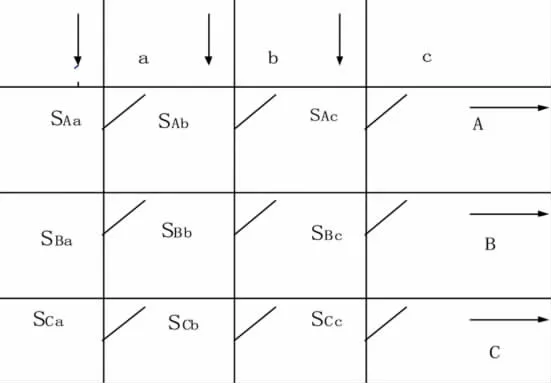
图1 三相－三相矩阵式变换器电路拓扑

由于矩阵变换器输入和输出直接相连，所以在任意时刻连接某一输出相的三个开关只能有一个导通；由于负载一般呈现感性，不能开路，所以在任意时刻连接至某一输出相的开关必须有一个导通。基于双向开关状态存在上述的限制，实际运行中必须根据控制目标的需要，采用一定的调制策略来选择相应的开关状态。本文采用双空间矢量调制策略，矩阵变换器采用间接数学模型，即将矩阵变换器的控制等效为“虚拟整流”和“虚拟逆变”两部分，如图2所示。

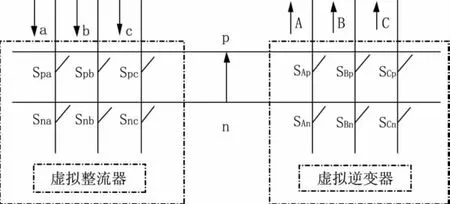
图2 矩阵变换器等效交－直－交结构图

2 双空间矢量调制策略

依据空间矢量调制原理，将“虚拟整流器”输入相电流空间矢量调制和“虚拟逆变器”输出线电压空间矢量调制结合起来，从而得到输入相电流和输出线电压的正弦波形，并且得到所需任意可控的输入功率因数。输入功率因数可根据预设定的输入相电压与相电流相位差得到。先考虑“虚拟逆变器”的输出线电压调制，矩阵变换器输出线电压空间矢量可定义为：UoL＝（UAB＋UBCe＋j120°＋UCAe－j120°），其合成原理如图3（a），（b）所示。

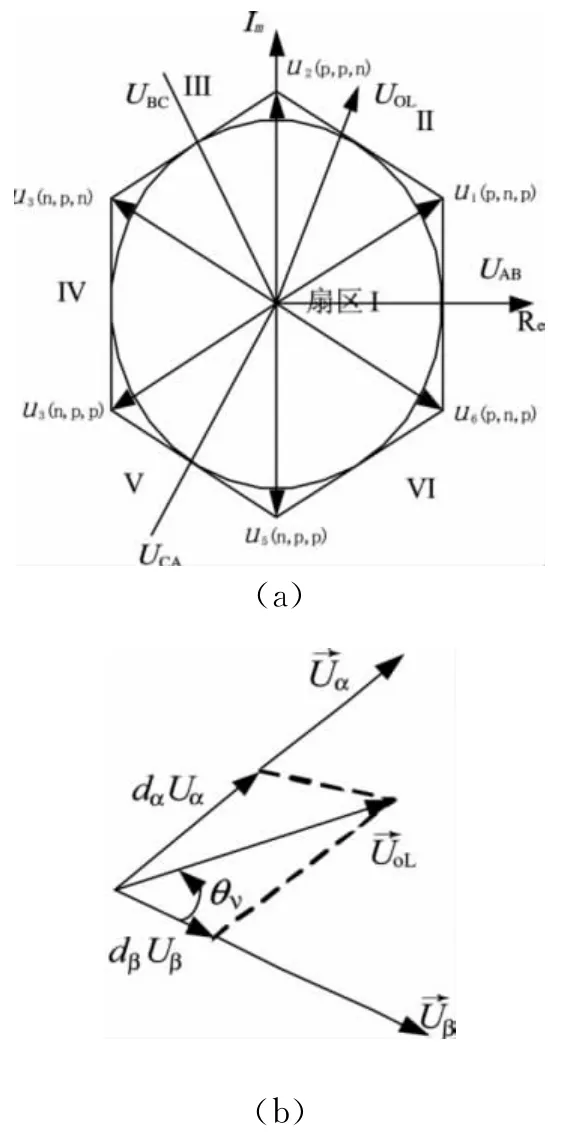
图3 输出线电压矢量调制

在某一时刻该空间矢量可由两个相邻的非零开关矢量Uα、Uβ和一个零开关矢量U0合成，扇区角θsv表示输出线电压空间矢量UOL在当前扇区中的位置，则各个矢量的作用时间根据正弦定理计算如下：

式中，Tα、Tβ、Tov分别为Uα、Uβ和U0在一个采样周期中的作用时间；TS为采样周期；mv是输出线电压空间矢量调制系数，其取值在0到1之间。

矩阵变换器输入相电流空间矢量调制过程与输出线电压空间矢量的调制类似。此时若输入相电流的空间矢量扇区角为θsv，则可得到开关矢量的作用时间如下：

式中，Tμ、Tv、Toc分别为，iμ、iv、和i0在一个采样周期中的作用时间；TS为采样周期；mc是输入相电流空间矢量调制系数，其取值在0到1之间。

在每个采样周期内，将输出线电压矢量合成与输入相电流矢量合成组合起来，共有5个开关状态Tαμ、Tβμ、Tβv、Tαv、T0，这5个开关状态在采样周期内的作用时间如下：

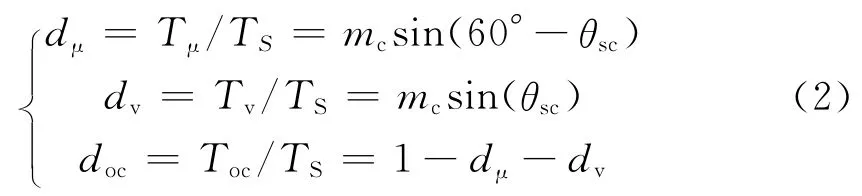
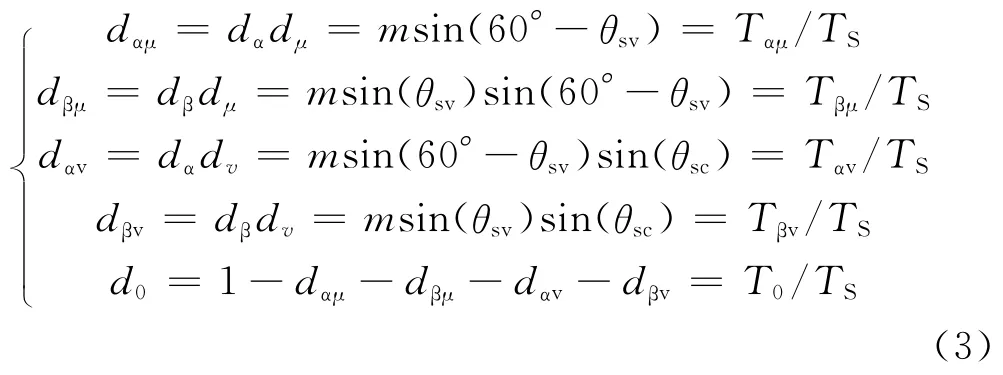
式中，m为矩阵变换器空间矢量脉宽调制系数，m＝mvmc。

双空间矢量调制法大多采用9段式PWM调制方式。文献［5］中介绍了可以使开关损耗达到最小的开关顺序，通过观察36种开关组合，按照下列顺序安排开关过程。

（1）当输入相电流扇区编号和输出线电压扇区编号之和为偶数时，开关过程一半为：

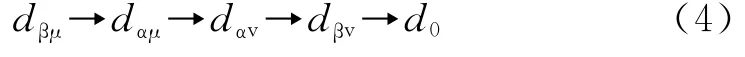
（2）当输入相电流扇区编号和输出线电压扇区编号之和为奇数时，开关过程一半为：

3 双空间矢量法的模型仿真

本文在MATLAB平台上进行仿真研究，根据以上描述的数学模型可以得到矩阵变换器的系统仿真模型。其中，扇区和扇区角计算、占空比计算、控制策略的实现采用S函数方法；主电路双向开关由理想开关搭建构造而成。仿真参数为输入电压220 V/50 Hz，输出频率50 Hz，负载为阻感负载，电阻10Ω，电感20 mH，输入功率因数设为1。矩阵变换器的仿真模型如图4所示。

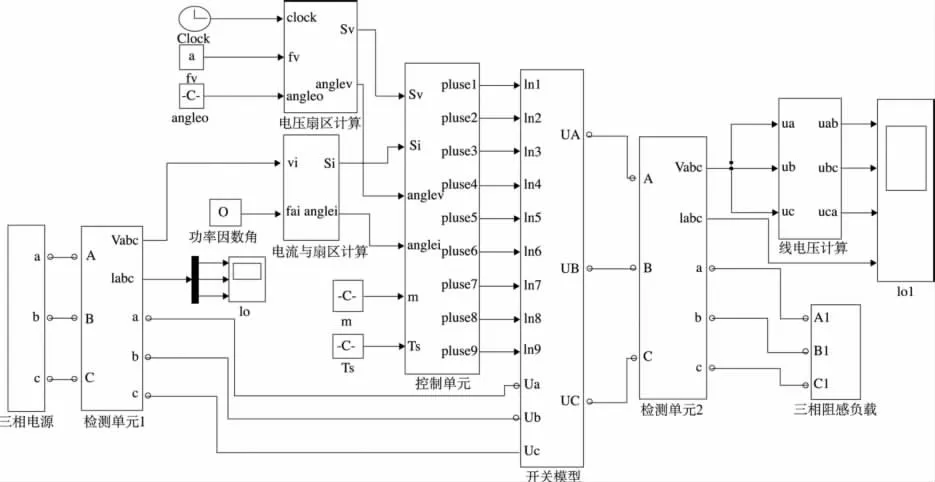
图4 矩阵变换器双空间矢量法的仿真模型

仿真结果输出线电压和输入相电流波形如图5（a）、（b）所示。

通过图5（a）、（b）可以看出，矩阵变换器输出侧线电压和输入侧相电流均为PWM波形，并且波形特性正确。仿真结果表明，本文对于矩阵变换器所搭建的系统模型和采用的算法具有正确性和可行性。但是由于矩阵变换器工作时存在开关频率附近的高次谐波，而上述仿真模型输入侧没有连接输入滤波器，所以输入相电流波形谐波含量比较丰富，这将会对输入侧电网造成谐波污染。因此在上述仿真模型的基础上，参照文献［10］中所介绍的矩阵变换器输入滤波器的设计方法，在输入端接入简单的三相LC滤波器。其中，在滤波电感上并联阻尼电阻以增加系统的阻尼比，提高系统的动态响应性能，同时降低输入滤波器的输出阻抗。再次进行仿真，此时输入相电流的波形如图6所示。

显然，图6与图5（b）相比，输入相电流谐波含量大大降低，更接近正弦波，大大降低了谐波污染。所以，只要接入合适的滤波设备，矩阵变换器可以获得理想的输入输出特性，有着比普通的PWM变换器更优异的性能。

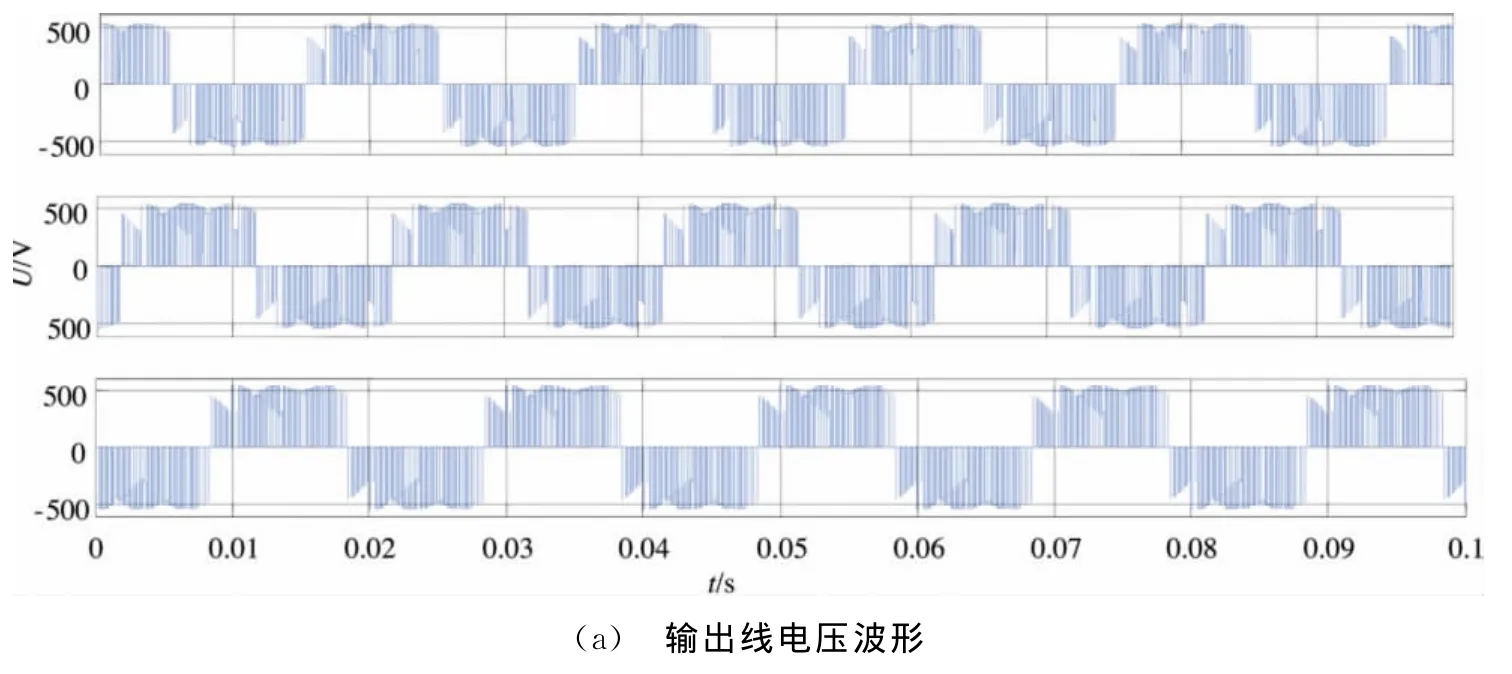
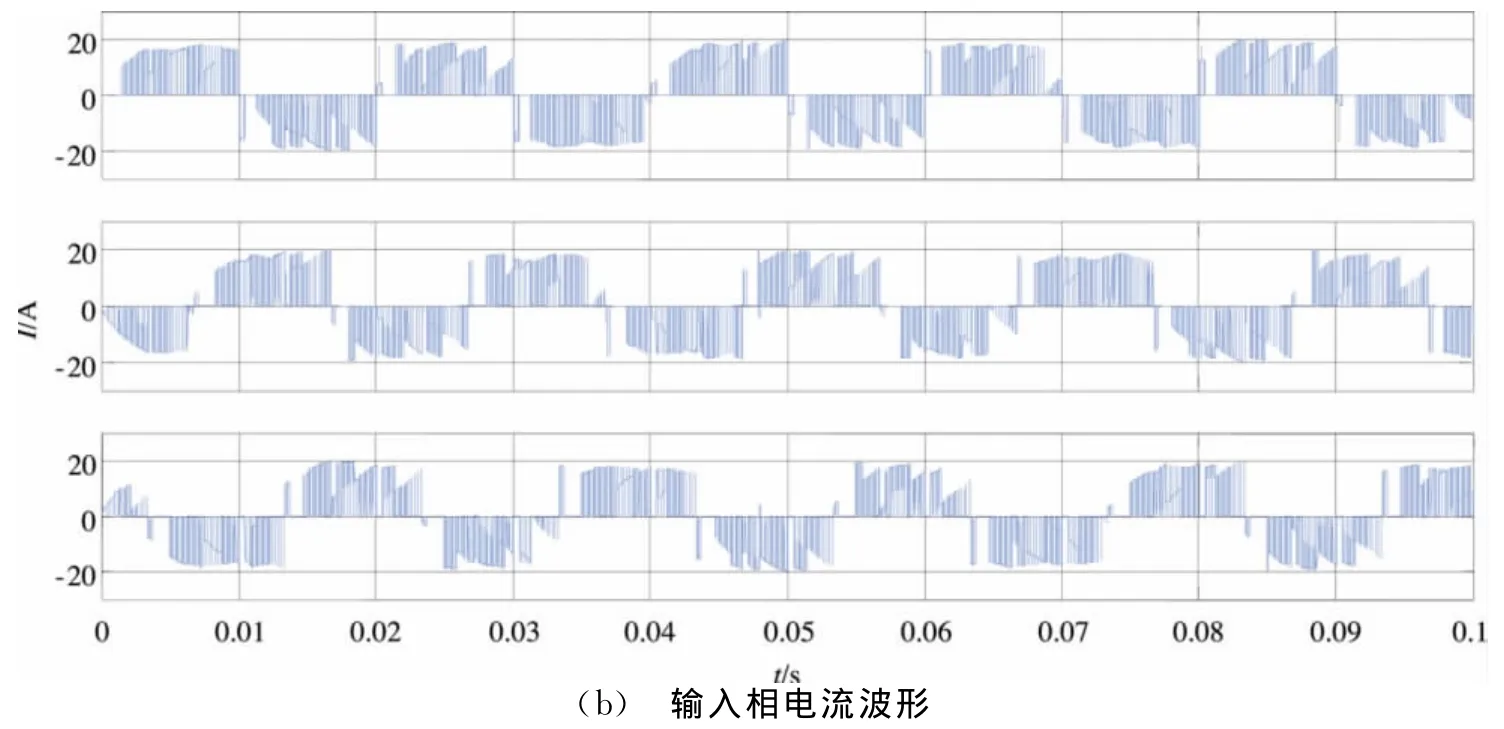
图5 仿真结果

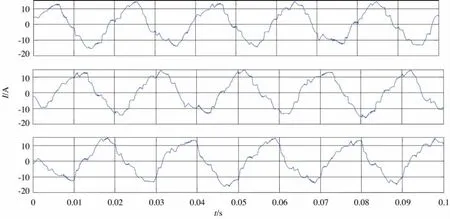
图6 滤波后的输入相电流波形

4 结 论

本文在研究矩阵变换器及双空间矢量调制法数学模型的基础上，建立了MATLAB/Simulink中仿真模型。仿真结果显示了矩阵变换器具有良好的输入输出特性，表明了文中对双空间矢量调制法所搭建模型及函数的正确性。另外，本论文还进行了更进一步的研究，简单设计了三相输入滤波器，并设置了相关参数。结果表明，接入输入滤波器后矩阵变换器仿真结果的波形特征显得更加优异。总之，文中运用双空间矢量调制法的矩阵变换器仿真模型是可行的，这为进一步研究由其控制的电机打下了良好的理论基础，并为进行电机控制的仿真系统奠定了相应基础。

［1］ 许东霞，李生民，孙旭霞.基于直接传递函数调制的矩阵变换器研究［J］.西安理工大学学报，2009，26（3）：360－363.

［2］ 杨喜军，龚幼民.矩阵变换器的理论与应用［M］.北京：机械工业出版社，2010.

［3］ 穆新华，庄心复.交－交型矩阵变换器的双电压控制原理及波形合成［J］.南京航空航天大学学报，1997，29（2）：151－157.

［4］ 孙 凯，周大宁，梅杨.矩阵式变换器技术及其应用［M］.北京：机械工业出社，2007.

［5］ 邓 伟，杨俊华，江艺芬.基于双空间矢量调制的矩阵变换器仿真研究［J］.研究与分析，2009，02（5）：17－20.

［6］ 佘宏武，林 桦.交－交直接变频矩阵变换器的研究与设计［J］.电机与控制应用，2007，34（3）：24－27.

［7］ Casadei D，Serr a G，T ani A.A general approach for the analysis of the input power quality in matrix converters［J］.IEEE Trans.on Power electronics 1998，13（5）：882－891.

［8］ Huber L，Borojevic D.Space Vector Modulated Threephase to Three－phase Matrix Converter with Input Power Factor Correction ［J］.IEEE Trans.on Ind.Applications，1995，31（6）：1234－1246.

［9］ 洪乃刚.电力电子和电力拖动控制系统的 Matlab仿真［M］.北京：机械工业出版社，2006.

［10］栗 梅，孙 尧.矩阵变换器输入滤波器的多目标优化设计［J］.中国电机工程学报，2007，27（1）：70－75.