基于滞环电流控制的串联型双Buck逆变器

李陆军，吕 青，姚国顺

（1.空军预警学院研究生管理大队，湖北 武汉430019；2.空军预警学院，湖北 武汉430019）

随着煤炭、石油和天然气等化石燃料的迅速消耗，以及由此带来的能源危机与环境污染日益加剧，近年来世界各国都在积极寻找新的可再生能源。在各种可再生能源中，风能和太阳能的利用最为广泛［1］。为了将这些能源有效地利用起来，逆变器是一个重要的环节。

桥式逆变器结构中，同一桥臂的驱动信号之间需加入死区，这一方面造成输出电压波形畸变；另一方面开关频率不能太高，使滤波电感和滤波电容都比较大，系统动态性能较差。采用双Buck半桥逆变电路能够解决此问题。其控制方法有SPWM和滞环电流控制方式等，由于Buck电路在负载较小时有可能工作在电流断续模式，造成输出电压波形畸变，所以在SPWM控制方式中需加入额外偏置电流信号，使滤波电感中始终有环流流过，系统效率较低。而采用无偏置电流半周期滞环电流控制方式能较理想地实现两个电感电流自然切换和半周运行［2］。

文中构造了串联型双Buck逆变器模型，提出了控制策略，通过电流内环控制两个串联双Buck逆变器的电感电流。电压外环用来调节逆变器最终的输出电压。本文分析了逆变器的工作原理及控制策略，进行了参数设计和仿真研究。

1 模型结构

图1给出了串联型双Buck逆变器的主电路，它由两个双Buck逆变器串联组成。光伏面板输出电压和风机整流输出电压分别作为两个双Buck结构的输入电压源。C1和C2、C3和C4是两对等值大电容，分别用来平分两个输入电压UIN1和UIN2。

图1 串联型双Buck逆变器主电路

2 工作原理

iref为参考电压Uref与输出电压反馈Uof之差经PI调节后产生的电流参考值。稳态工作情况下，参考电流iref在正半周时S1和S4工作，参考电流iref在负半周时S2和S3工作。因为逆变器1和逆变器2的工作原理相同，现以单个逆变器1为例分析滞环控制工作过程。主要波形如图2所示，其中Δ＝2h为滞环宽度，Uds1和Uds2分别是开关管S1和S2的漏源极间电压。

为方便分析，做如下假设：

（1）所有开关管和二极管都是理想的；

（2）所有电感和电容都是理想的；

（3）在一个开关周期内逆变器1的输出电压Uo1为恒值；

（4）输入电压UIN1大于输出电压最大值的两倍；

（5）Lf1＝Lf2＝L。

图2 单个逆变器主要工作波形

在每个周期内有四种开关状态，如图3所示。

2.1 iref＞0

这期间内S2一直关断，iL2恒为0，Lf2上电压也为0，所以Uds2为（UIN1/2＋Uo1），D2上的电压为（UIN1/2－Uo1）。S1工作在高频状态。

（1）状态1：如图3（a）所示，当滤波电感Lf1的反馈电流if1＜iref－h时，S1开通，iL1线性增加。这期间

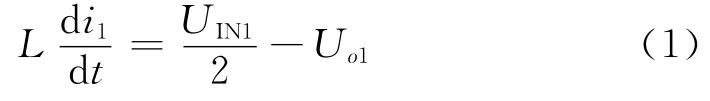
（2）状态2：如图3（b）所示，当滤波电感Lf1的反馈电流if1＞iref＋h时，S1关断，D1导通续流，iL1线性减小。这期间

由式（1）、（2）得

其中d1是S1的占空比。

2.2 iref＜0

这半个周期内，S1一直关断，iL1恒为0，Lf1上电压也为0，所以Uds1为（UIN1/2－Uo1），D1上的电压为（UIN1/2＋Uo1）。S2工作在高频状态。

（1）状态3：如图3（c）所示，当滤波电感Lf2的反馈电流if2＞iref＋h时，S2开通，iL2反向线性增加。这期间

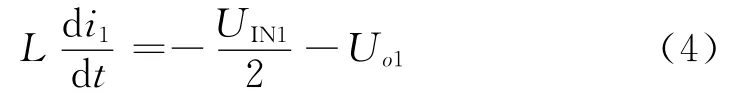
（2）状态4：如图3（d）所示，当滤波电感Lf2的反馈电流if2＜iref－h时，S2关断，D2导通续流，iL2反向线性减小。这期间

由式（4）、（5）得

其中d2是S2的占空比。

图3 单个逆变器四种工作状态

3 控制策略

图4（a）所示为滞环电流控制原理，KP和KI分别是外环输出电压调节器的比例系数和积分系数，其中KP取值为6，KI取值为54 000。iref是输出电压采样Uof与参考电压Uref相比较后经PI调节器产生的参考电流。Uc是iref经过零比较后产生的方波，iref为正时Uc是高电平，iref为负时Uc是低电平，它用来控制四个开关管，使参考电流iref在正半周时S2和S3一直关断，S1和S4正常工作；iref在负半周时S1和S4一直关断，S2和S3正常工作。

图4（b）所示是串联型双Buck逆变器的系统控制框图。其中，K1是滤波电感电流的反馈系数，K2是系统输出电压的反馈系数，K1取值为0.2，K2取值为0.03。Go1（s）和Go2（s）分别是两个逆变器单元的输出阻抗传递函数。频率较高时系统框图中的滞环控制电流环可以等效成放大倍数为1/K1的增益环节［3］。

图4 控制策略

4 参数设计

逆变器1和2具有相同的设计思路，并且各项参数也相同，这里设计其中一个。

4.1 输出要求

串联型双Buck逆变器输出电压要求为Uo＝220 V，频率fo＝50 Hz，额定功率为Po＝2 kW，所以额定负载阻抗R＝24.2Ω。

4.2 输入电压

两个输入源电压必须都要大于逆变器最大输出电压的两倍，这样，要先将光伏电和风电经初步变换使二者为700 V直流电，即UIN1＝UIN2＝UIN＝700 V。

4.3 开关频率

通过式（1）、（2）可得开关管开关频率fs为

式中，h1＝2h/K1。

根据上式可知，最大开关频率发生在Uo1＝0时，最小开关频率发生在Uo1＝时。

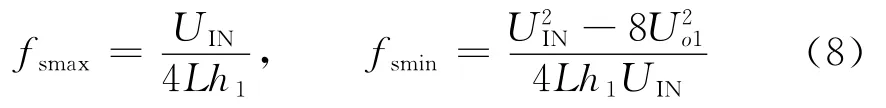
式中，Uo1是电压Uo1的方均根值。开关管的最高频率不能太高，不然会有较大的损耗，而且可能因为温度过高烧坏开关管，开关管最高开关频率选定在80 kHz。

开关的平均频率可估计在

4.4 滞环宽度

由式（8）前式可见，当UIN和fsmax固定时，L和h1的乘积为定值，为了减小电感体积和重量，h1要尽量取大，但同时h1太大会引起较大的电流波动，降低跟踪精度。故选择滞环宽度为输出电流值的一半。

计算得h1可选择4.5A。

4.5 滤波电感

在UIN、fsmax和h1都选定后，滤波电感值由下式计算得出：

计算得L选择在490μH。

4.6 滤波电容

滤波电容可以通过LC滤波器的转折频率来设计。转折频率应该高于输出电压频率fo的10～20倍，且应该低于开关管平均频率fsav的1/20～1/10［4］。所以转折频率应该高于500 Hz，低于4 kHz。选择滤波器转折频率在中间位置，即2.5 kHz。滤波电容可由下式得出：

可选滤波电容为10μF。

5 仿真和实验

按照上述设计参数进行模型仿真。图5（a）所示为UN1＝UIN2＝700 V时额定负载下的仿真波形。从上至下波形依次为iL1、iL2、iL3、iL4和Uo。四个电感电流大小相同，相对平衡。图5（b）所示为UIN1＝630 V，UIN2＝700 V时额定负载下的仿真波形。从中可看出当一个输入电压较低时，对应的输出电流会发生微小变化，但输出电压仍然稳定。图6给出了UIN1＝630 V，UIN2＝700 V时额定负载下的实验波形，其中（a）是开关管S1的驱动波形，（b）是iL1与iL2之和的反馈波形，（c）是输出电压波形Uo。

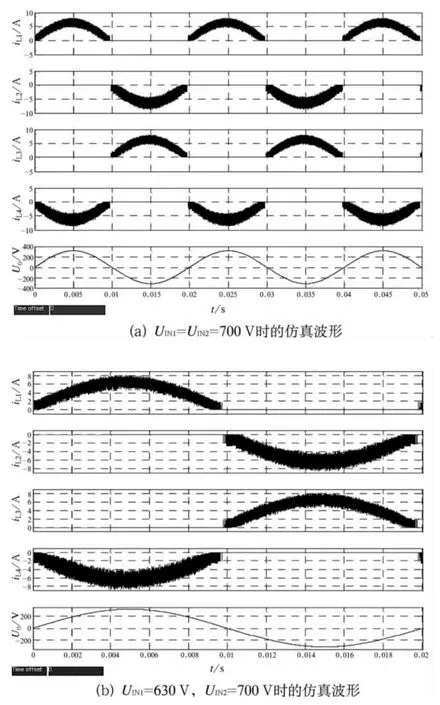
图5 仿真波形

图6 实验波形

6 结 论

本文研究了基于滞环控制的串联型双Buck逆变器的工作方式，设计了仿真参数，分析了不同输入下的仿真输出波形。结果表明该系统具有比较好的动态和稳态性能，在输入电压不稳的情况下能保证输出电压有高的正弦度。可以用于分布式发电系统，有工程实际应用价值。

［1］ 陈 岚，史伟伟.并网型风光互补发电系统的研究现状［J］.机电信息，2010，（36）：3－4.

［2］ 张先进，王慧贞.双Buck半桥逆变器研究［J］.电源世界，2004，（5）：57－59.

［3］ 王建华，张方华，龚春英，等.滞环电流控制逆变器建模及分析［J］.电工技术学报，2010，25（6）：63－69.

［4］ Mazumdar J，Batarseh I，Kutkut N.High frequency low cost DC－AC inverter design with fuel cell source for home applications［C］.IEEE Ind.Appl.Conf.，2002：789－794.