开关变换器补偿网络的频域设计与仿真

于岳川

（武汉大学电气工程学院，湖北 武汉 430072）

0 引 言

开关电源以其效率高、尺寸小、重量轻等优点，广泛应用于各个领域。为了保证开关电源输出电压的质量，需要对开关变换器设计补偿网络。本文以Buck电路为例，讨论电压控制型开关调节系统补偿网络的设计与仿真。与其他控制方式相比，电压控制型开关调节系统具有控制方式简单、稳定、易于设计等优点，同时也可以保证很好地稳压精度［1］。

1 开关变换器补偿网络的频域设计步骤

根据经典控制理论，开关调节系统频域设计步骤可总结为：（1）确定系统的控制方法；（2）绘制变换器的开环传递函数bode图；（3）根据变换器开环传递函数的特点，结合对系统性能指标的要求，选择合适的补偿网络类型；（4）确定补偿网络参数；（5）校验补偿后系统的性能。为叙述方便，将电压采样网络和补偿网络合并，称之为电压控制器。将电压控制器以外的环节合并，称之为控制对象。再根据控制对象的特点，合理选择补偿网络的类型，并结合系统对稳态精度和动态性能以及稳定裕度的要求，确定补偿网络参数。

2 Buck电路的补偿网络设计

设Buck电路工作在CCM模式下，电路的参数为：输入电压Ug＝16 V，滤波电容C＝500μF，电容等效串联电阻RC＝8 mΩ，储能电感L＝500μH，电感等效电阻RL＝50 mΩ。输出电压Uo＝6 V，负载电阻1 Ω，参考电压Uref＝6 V，PWM发生器锯齿波幅值UM＝2.8 V，开关频率50 kHz。非理想Buck电路如图1所示。

图1 非理想Buck电路

设计步骤如下：

步骤1 设计电压采样网络。由于在直流频率点，系统为深度负反馈系统，故电压采样网络传递函数

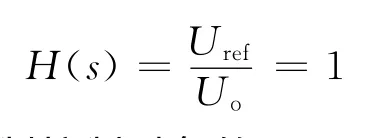
步骤2 绘制控制对象的bode图：对于本文的非理想Buck电路，其控制－输出的传递函数为［1］：

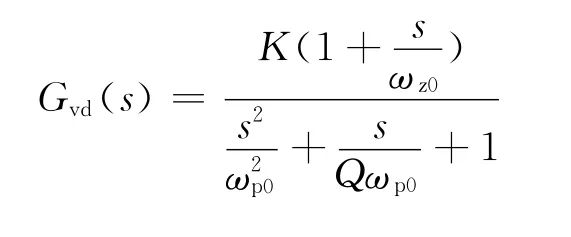
其中：

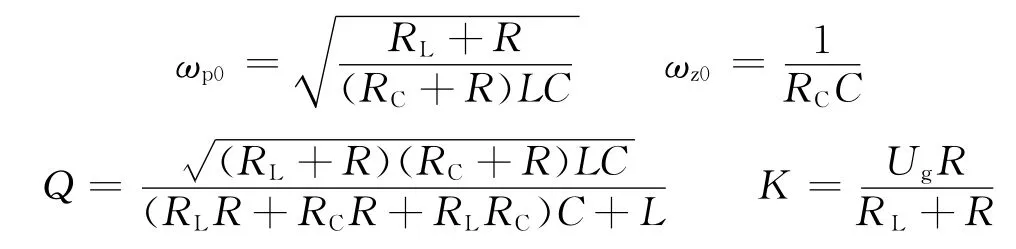
式中，ωz0为电容的ESR零点。代入数据得到控制－输出的传递函数为：

由MATLAB得到传递函数开环bode图，如图2所示。

图2 补偿前系统开环bode图

由图2可以看出，低频段的斜率为零，说明系统存在稳态误差；相位裕度为13°左右，稳定程度不够；在高频段的斜率为－40 dB/dec，对高频噪声的抑制能力较好。鉴于此，需引入补偿网络，使各个频段的特性得到改善。

步骤3 补偿网络的设计

鉴于步骤2中的分析，为了改善系统的稳态精度，需要使系统在低频段以－20 dB/dec的斜率下降，故补偿网络需要包含积分环节；为了拓宽频带并且增加相位裕度，需要在剪切频率之前的频段增加两个零点；为抵消ESR零点对电路性能的影响，需引入一个极点与ESR零点抵消。同时为了保证高频抗干扰能力又不至于引入过多的相位滞后，需要在高频段再引入一个极点。综合以上的分析，选择双极点－双零点型PID补偿网络，其对应电路（图3）及传递函数形式如下：

确定参数如下：

为了提高穿越频率，设补偿后系统开环传递函数的幅值穿越频率为开关频率的1/6，即fc＝50/6＝8.3 kHz左右。为了得到足够的相位裕量，希望补偿网络在此频率附近提供最大的超前相位。

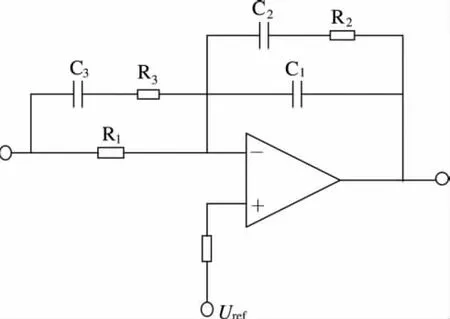
图3 双极点－双零点型PID补偿网络

第一零点应能提供足够的超前相位以提高稳定裕度，故第一零点应取的较小。取第一零点角频率ωz1＝100 rad/s；第二零点主要起到拓宽频带的作用，因此应取较大值，但是不能超过ωc，取ωz2＝30×103rad/s。

第一极点用于抵消ESR零点的作用，故取第一极点为角频率ωp1＝ωz0＝2.5×105rad/s；第二极点用于提高系统抗高频噪声的能力，取ωp2＝1.5×105rad/s。由以上确定的各参数计算PID控制器各元件的参数如下：

取R1＝100 kΩ，则其他元件参数为：R2＝500 kΩ，R3＝1.2 kΩ，C1＝13 pF，C2＝20 nF，C3＝3.33 nF。进而确定K1＝500。

由MATLAB得到补偿网络的bode图，如图4。

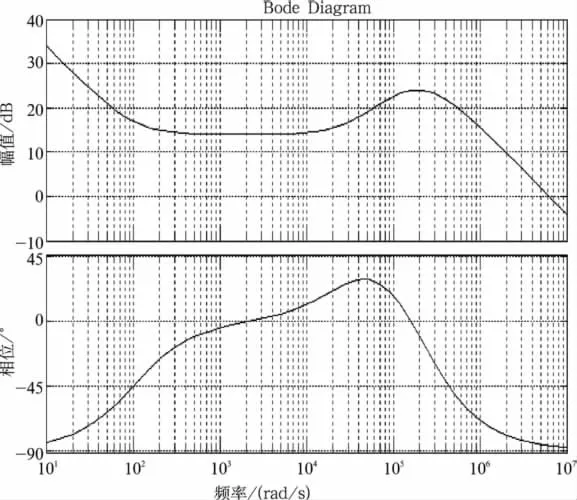
图4 补偿网络的bode图

由图4可得，该补偿网络在7.7 kHz附近提供的最大超前相位角，与设计初衷吻合。

由以上结果可得到加入补偿网络后系统的开环传递函数表达式为：

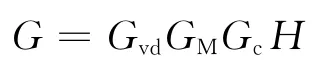
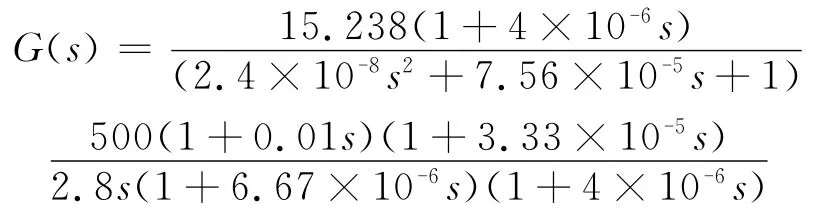
由MATLAB得到加入补偿装置后系统的bode图，如图5。

图5 补偿后系统开环bode图

由图5可得：校正后系统的穿越频率fc＝7.1 kHz，相位裕度约为45°，符合设计要求。

3 闭环系统的simulink仿真

为了验证补偿网络的合理性，根据以上计算所得的传递函数，应用simulink中PowerSystems工具箱搭建仿真电路图如图6。

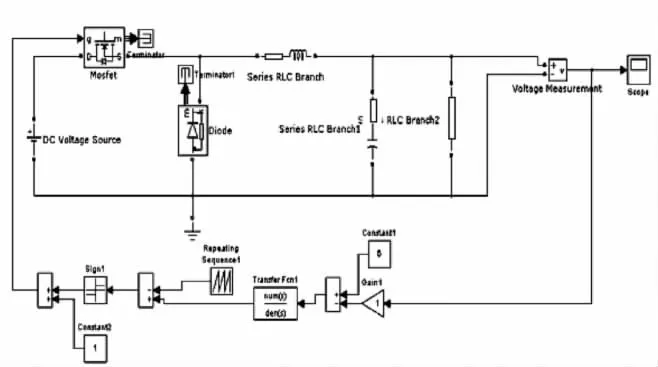
图6 simulink电路仿真模型

为了测试加入补偿网络后系统的性能，分别作如下实验：

（1）在0.07 s负载突然加倍；（2）在0.07 s输入电压由18 V跃变到16 V；实验结果如下。

图7为负载扰动的情况，图8为输入扰动的情况。图中曲线1为未加补偿时输出电压波形，曲线2为加入补偿后输出电压的波形。根据仿真结果，得到系统的性能指标如表1和表2所示。

表1 负载扰动时系统性能指标

图7 输入扰动时输出电压波形

图8 负载扰动时输出电压波形

表2 输入扰动时系统性能指标

表中ts为暂态恢复时间，Uo%为电压稳定度，ΔUo为过冲电压。由表1和表2可见，加入补偿网络后，系统的响应速度和稳态精度都有了明显的改善。

4 结 论

本文采用频域法对电压型调节系统进行了设计，其主要思路是：根据对系统性能的要求（快速性、准确性、稳定性），结合系统的开环bode图对补偿网络进行设计。系统开环bode图的低频段决定了系统的稳态精度，中频段决定了系统的稳定裕度及响应速度，高频段决定了系统抗高频噪声干扰的能力。在设计时应结合控制对象的特点设计补偿网络各个频段的参数，合理配置补偿网络零极点的位置，使系统获得较好的性能指标。从仿真结果来看，加入补偿网络后系统性能得到了改善，与理论分析结果相一致，验证了设计的合理性。

［1］ 张卫平.开关变换器的建模与控制［M］.北京：中国电力出版社，2006.

［2］ 胡寿松.自动控制原理（第5版）［M］.北京：科学出版社，2007.

［3］ 林 飞，杜 欣.电力电子应用技术的 MATLAB仿真［M］.北京：中国电力出版社，2009.

［4］ 余明杨，蒋新华，王 莉，等.开关电源的建模与优化设计研究［J］.中国电机工程学报，2006，26（2）：165－169.

［5］ 陈亚爱.开关变换器的使用仿真与测试技术［M］.北京：机械工程出版社，2009.

［6］ Ruzbehani M，Zhen Louwei，Wang Mingyu.A new approach in combining one－cycle controller and PID controller［C］.Industrial Electronics，2004 IEEE International Symposium on Volume 2，May 2004：1173－1177.

［7］ Ridley R B.A new，continuous－time for current－mode control［J］.IEEE Transactions on Power Electronics.1991，6（2）：271－280.