基于非局部均值的图像降噪
祁国平,吴朝润
(1.中北大学电子测试技术国家重点实验室,山西太原030051;2.中北大学信息与通信工程学院,山西太原030051)
图像降噪方法的目的是从噪声图像中恢复原始图像,

其中,v(i)是观察值,u(i)是真实值,n(i)是像素i上的噪声干扰。在数字图像上建立噪声模型[1]的最简单方法是添加高斯白噪声。在这种情况下,n(i)是均值为0,方差为σ2的高斯白噪声。
很多降噪和恢复原始图像的方法提出,它们虽然在降噪方法上不同,但被广泛应用的理论是:消噪通过平均[2]来实现。局部平均方法:高斯平滑模型,邻域滤波;频域:经典维纳滤波[3],小波阈值方法[4]。
我们定义消噪方法Dh作为一个分解:v=Dhv+n(Dh,v),其中v是噪声图像,h是滤波参数决定噪声的标准偏差。理想的Dhv比v平滑,n(Dh,v)为白噪声。图像平滑部分和非平滑部分的分解是目前的研究课题。消噪的方法不应该改变原始图像u。现在,大多数的降噪方法移除了u的细节和纹理。
1 非局部均值算法
本文中我们提出非局部均值算法,公式如下:
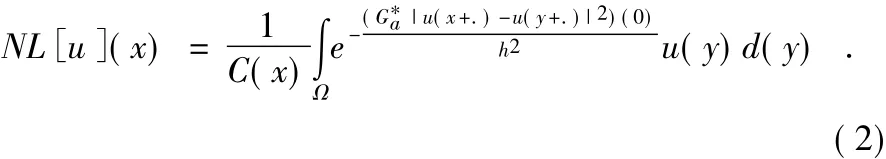
离散噪声图像v={v(i)|i∈I},像素i的估计值NL[v](i),通过所有像素的加权平均来计算。
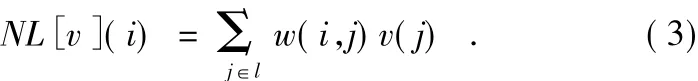
其中{w(i,j)}j决定像素i和像素j的相似性,满足
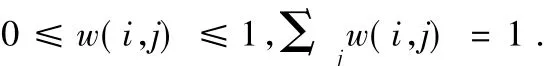
像素i和j的相似性决定灰度矢量的强度v(Ni)和v(Nj)之间的相似,其中Nk为固定邻域大小的平方,中心为像素k。这个相似通过欧氏距离加权减少功能测量,‖v当a>0时是高斯核心的标准偏差。应用欧氏距离是为了提出噪声邻域的等式:
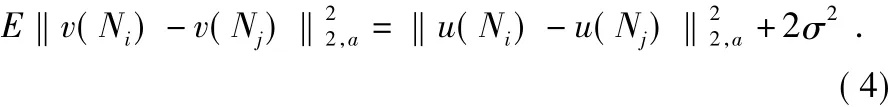
这个等式表示算法的强大,因为在欧氏距离期望中不需要像素间相似的次序。
v(Ni)中具有相似灰度邻域的像素有较大的权重平均。如图1,权重计算如下:
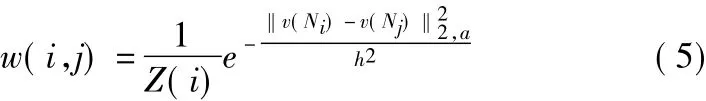
非局部均值不仅比较单一点灰度,而且比较整个邻域的几何组态。这个事实允许比邻域滤波更强大的比较。图1中,像素q3与像素p有相同的灰度值,但是邻域有很大的不同,因此,权重 w(p,q3)接近于0。

图1 非局部均值战略
2 非局部均值的一致性
平稳假设,一个像素i,非局部均值算法收敛于i的条件期望。这种情况下,平稳条件下数量是图像增长的大小,我们可以为图像的细节找到很多相似块。
设V是随机领域,假设噪声图像v是V的实现。Z为随机变量序列Zi={Yi,Xi},其中,Yi=V(i)是真实值,Xi=V(Ni{i})是iP估值。非局部均值是条件期望:

定理说明非局部均值算法纠正噪声图像而不是从真实图像中分离噪声。
假设添加白噪声模型,下一步结果表明条件期望是V(Ni{i})的功能,最小化真实图像u的均值平方误差。
定理2 V,U,N是随机领域I上,V=U+N,N为独立的白噪声信号,
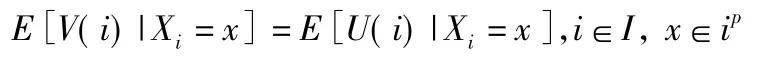
3 实验结果及分析
在matlab中实现不同标准偏差下非局部均值降噪,以及降噪处理后的图像噪声对比,最后用结构相似度SSIM和峰值信噪比PSNR对提出的算法进行评价。
非局部均值算法,我们限制在大的搜索窗口中的相似搜索窗口大小S*S像素。在所有的实验中我们固定搜索窗口为21*21像素,相似平方邻域Ni为7*7像素。如果N2为图像像素的数量,算法的最后复杂度为49*441* N2。
图2为lena原图,图3是不同标准差下非局部均值的降噪效果图,图4是不同标准差下非局部均值算法的噪声层。

图2 lena原始图像

图3 不同标准差下非局部均值降噪的降噪效果图

图4 不同标准差下的非局部均值的噪声层
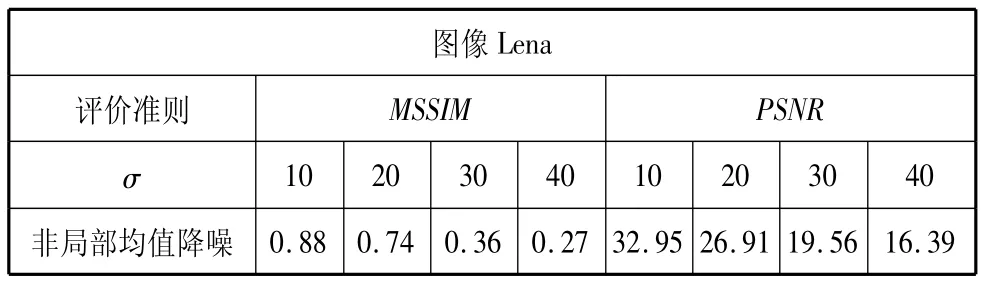
表1 图像Lena非局部均值降噪的MSSIM和PSNR结果
由图3和图4可以看出,随着标准偏差σ的增大,噪声成分增多,非局部均值的降噪效果没有σ较小时好,但其保持了较好的纹理和细节。
由表1可以得到结论,随着标准偏差σ的增大,峰值信噪比PSNR逐渐减小,而结构相似度[5]也随之减小,这也同样体现了图3和图4的效果即噪声成分增多。
4 结论
实验结果显示基于非局部均值的图像降噪算法在结构相似度和峰值信噪比的评价算法上具有较明显的去噪效果。尽管其在消噪方面很有效,但在消噪输出时包含很多的视觉伪影。今后的工作是近一步寻求去噪效果更好的算法。
[1]A.Buades,B.Coll,and J.Morel.Neighborhood Filters and Pde’s[R].Technical Report 2005 - 04,CMLA,2005.
[2]K.Dabov,A.Foi,V.Katkovnik,and K.O.Egiazarian.Image Denoising by Sparse 3-D Transform-domain Collaborative Filtering[J].IEEE Trans.Image Process,2007,16(8):2080 -2095.
[3]Yanmin He,Tao Gan,Wufan Chen,and Houjun Wang.Adaptive Denoising by Singular Value Decomposition[J].IEEE SIGNAL PROCESSING LETTERS,2011,18(4):215-218.
[4]姜三平.基于小波变换的图像降噪[M].北京:国防工业出版社,2009.
[5]吴秀英,胡海平.基于小波变换和人眼视觉系统特性的图像降噪方法[J].应用数学与计算机数学学报,2011,25(1):74 -79.

