热加工条件下Ti60高温钛合金的本构关系

孙二举， 边丽虹， 刘 东， 焦 园， 张 睿

（1.西北工业大学，西安710072;2.中航工业沈阳黎明航空发动机（集团）有限责任公司，沈阳 110043）

钛合金因其低密度、高强度、耐热性好等特点［1］，是航空发动机中的关键结构材料［2］。因而，进一步提高钛合金部件的使用温度是钛合金技术领域的重要发展方向。目前高温钛合金的使用温度已经达到了600℃，比较典型的高温钛合金主要有IMI834，Ti1100，BT36，Ti60 等［3］。目前已经应用的多数高温钛合金均属于Ti-Al-Sn-Zr-Mo-Si系近α钛合金。其中，Ti60合金是我国自主研发的一种能够在600℃下长期工作的高温钛合金，其合金化特点是严格控制O含量，适当调整Al，Sn，Si含量，并添加了一定的稀土元素Nd（≤1%，质量分数），从而获得了优异的热强性和热稳定性，综合性能相当于IMI834合金。

由于Ti60合金合金化程度高，加工窗口狭窄，锻件的组织性能对热加工过程十分敏感，为了获得所需的组织性能需严格控制加工工艺和成形过程。材料的本构关系是联系流动应力与锻造热力参数之间的最基本函数关系，是进行金属塑性变形工艺设计和理论分析的基础［4］。对于Ti60合金，其在热加工参数范围内的本构关系研究相对较少，因此，建立精确的、合理的本构关系对Ti60合金锻造工艺设计和过程控制非常重要。

材料的本构关系通常有两种形式:机理型本构关系和唯象型本构关系。机理型本构关系［5］侧重于描述变形过程的微观机理，是从高温变形的物理机制出发建立起来的物理模型。这种本构关系一般需要涉及多个描述微观变形机制的参数，测试和应用相对困难。唯象形本构关系［6］是利用数理统计的方法对试验测量的一定应变速率、温度范围内的流动应力数据进行统计分析，建立经验或半经验的唯象流动应力模型，此模型形式简单，精度较高，应用容易。本工作即采用数理统计的方法根据等温恒应变速率压缩试验数据建立Ti60合金的唯象型本构关系，从而为热加工条件下Ti60合金成形过程数值模拟和锻件质量控制提供基础。

1 试验材料和方法

试验材料为Ti60合金锻制棒材，其名义化学成分如表1所示。实测相变温度为1050℃。其原始微观组织如图1所示。由图1可知，Ti60合金原始组织由等轴初生α相和β转变组织组成，初生α相尺寸约30μm左右，体积分数约为60% ～70%。

表1 Ti60合金的名义化学成分（质量分数/%）Table 1 Chemical composition of Ti60 alloy（mass fraction/%）

Ti60 alloy

采用Gleeble-3500热模拟试验机进行等温恒应变速率压缩试验，以获得所研究材料的流动应力随应变速率、等效应变和变形温度的数据。试样加工成φ8mm×12mm的圆柱体，上下两端面加工有0.2mm的浅槽以存贮润滑剂。试样压缩时，采用试验机专用润滑剂进行端面润滑。在整个试验过程中，试验机自动采集和计算载荷、位移、真应力与真应变的数据，以图形和数据表格的方式输出试验结果。试验方案如下:变形温度为:960℃，990℃，1020℃，1050℃，1080℃;应变速率为:0.01s-1，0.1s-1，1s-1，10s-1;保温时间为 10min;变形量均为60%;冷却方式:水冷。每个规范两个试样。

2 试验结果讨论与分析

2.1 热力参数对流动应力的影响

图2分别为Ti60合金不同变形温度和应变速率条件下变形的应力-应变曲线（相同条件下两个试样的应力非常接近，图中所示应力为两个试样应力的平均值）。从图中可以看出，在试验温度范围内，Ti60合金的应力随着应变的变化特征基本接近。变形开始时，应力随着应变的增加呈近直线关系迅速增大至峰值，随着变形温度的升高和应变速率的降低，峰值应力逐渐减小。随后，在变形温度和应变速率的影响下，应力随着应变的增加有不同程度的下降。随着应变的继续增大应力软化程度逐渐减小，流动应力趋于稳定，材料进入稳态变形阶段。

应该指出，对于本研究采用的Ti60合金，在材料发生屈服时均存在不同程度的应力突降现象。在试验温度和应变速率范围内，应力突降的程度随温度的升高和应变速率的降低而减小。一般认为，钛合金在屈服点附近的应力突降现象可用静态理论和动态理论来解释［7］，前者主要与位错的“钉扎”和“解脱”作用有关，后者则认为主要与可动位错的突然增殖有关。作者认为，除了前述两种理论外，出现应力突降现象还应该充分考虑材料成分和组织构成的影响。对于Ti60这类高温钛合金，为了获得理想的热强性和高温蠕变性能，一般均加入了较高含量的Si。热加工过程中，硅化物主要以细小颗粒的形式在β转变组织中弥散析出，从而明显增强了位错的“钉扎”作用和“位错增殖”作用。这也是Ti60合金与其他种类钛合金相比，屈服点应力突降现象更显著的内在原因。

图2 Ti60合金的应力-应变曲线Fig.2 Stress-strain curves in the isothermal compression of Ti60 alloy （a）T=960℃;（b）T=1020℃;（c）T=1080℃

在温度不变时，随着应变速率的升高，材料的流动应力显著升高，表现出较强的应变速率敏感性。其主要原因是随着应变速率的增加，单位应变所需要的时间缩短，位错增殖和运动速度增加，由位错引起的加工硬化作用更加明显，使得材料的流动应力增大。对于不同的应变速率，Ti60合金的应力-应变曲线表现为不同的流变特性:应变速率较高时（≥1s-1），流动应力经过明显的加工硬化达到最大值后逐渐减小;应变速率较低时（≤0.1s-1），流动应力达到最大值后基本保持不变，这主要是由于应变速率低，变形持续时间长，加工硬化效应能够更充分地被再结晶等软化过程抵消，同时，应变速率低，热效应不明显，因而流动应力基本达到一个平衡状态。

在应变速率不变时，随着变形温度的升高，材料的流动应力逐渐降低，同样表现有较强的温度敏感性。分析其原因是变形温度的升高，原子热振动的振幅增大，原子的平均动能增大，晶体产生滑移的临界分切应力减小，材料的位错运动和晶间滑移阻力降低，变形过程中的软化作用加强，抵消了塑性应变造成的加工硬化，从而促使材料流动应力减小。

2.2 本构关系形式的选择

在金属及合金的热变形行为研究中，材料的本构关系广泛采用 Arrhenius型方程表示［8，9］:

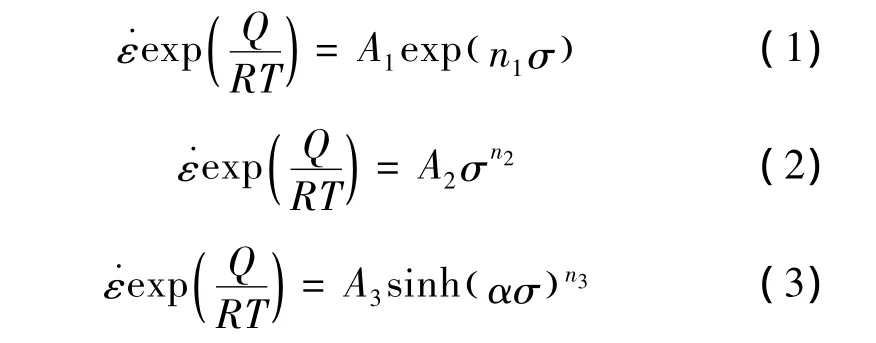
上述三种Arrhenius型方程根据流动应力出现的形式分别称为指数方程、幂函数方程和双曲正弦方程，对（1）至（3）式两边取对数后可表达为统一形式:

对应于式（1）至（3），式中f（σ）分别表示 σ，lnσ，ln［sinh（ασ）］;A，B，C，分别表示各方程中相应的系数项。由式（4）可知，对于给定的等效应变速率和变形温度，f（σ）分别为ln˙（）ε和1/T的二元线性函数。因此，将流动应力数据按式（4）进行处理，所表现出的线性关系越强，则本构关系的计算精度越高。图3和图4分别为峰值应力条件下f（σ）与ln˙

（）ε和1/T对应关系图。从图中可以看出f（σ）按式（4）处理后的试验数据均不同程度地表现出与ln˙

（）ε和1/T的高次函数关系。其中，幂函数方程的线性关系要优于其它两种方程。因此，本研究在建立Ti60合金本构关系时，选取幂函数方程为基础。同时，为了充分表征Ti60合金试验数据所表现出的高次函数关系，在幂函数型Arrhenius方程基础上，引入 Zener-Hollomon参数［10］的高次项，以进一步提高本构关系的计算精度。具体方程形式如下:

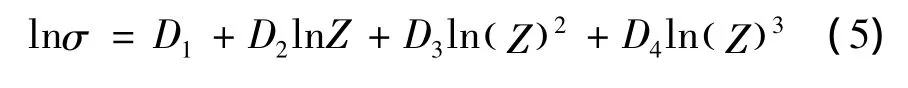
图3 f（σ）与ln（˙ε）对应关系Fig.3The relation between f（σ）and ln（˙ε）（a）exponent equation;（b）power function equation;（c）hyperbolic sinh equation

2.3 本构关系建立

本构关系模型含有Zener-Hollomon参数，需首先确定变形激活能Q。对式（2）两边取自然对数整理得:

在一定的应变和应变速率下对式（6）两边求导得:

在一定的应变和温度条件下对式（6）两边求导得:

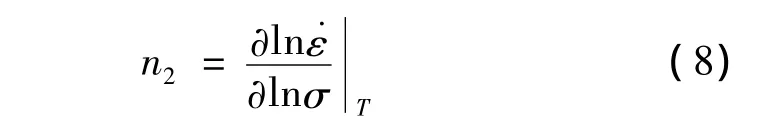
由式（7）和（8）可知，n4可由lnσ与1/T直线斜率的平均值求得，n2可由lnσ与ln直线斜率倒数的平均值求得。通过R，n2和n4的值，由式（7）可求得变形激活能。经计算Ti60合金的平均变形激活能Q=4.608 ×105J/mol。

对Zener-Hollomon参数取自然对数可得:

各试验规范下，ln（Z）的值可由式（9）求得。根据等温恒应变速率压缩试验数据按式（5）回归处理，即可确定式中系数D1，D2，D3，D4与应变的关系，如图5所示。

对给定应变下系数D1，D2，D3，D4的计算值进行多项式拟合，可确定各系数与应变的关系，各系数的表达式和相关系数如表2所示。

表2 系数D1，D2，D3，D4表达式和相关系数Table 2 The expressions and R-Square of D1，D2，D3，D4

2.4 本构关系验证

图6所示为试验测得的峰值应力按式（5）进行回归分析的结果。从图中可以看出，式（5）可以很好的描述Ti60合金峰值应力的变化规律。图中数据点为试验结果，曲线为采用式（5）的计算结果。

采用所建立的本构关系计算得到的不同变形条件下的流动应力曲线及其与试验数据的对比示于图7。误差分析结果表明，试验温度条件下流动应力计算值与试验值之间的相对误差小于10%。因此，上述建立的本构方程较准确的描述了Ti60合金热态变形时流动应力的变化规律。

图6 Ti60合金峰值应力与参数Z的关系Fig.6 The ln σp-lnZ curves of Ti60 alloy

图7 Ti60合金流动应力试验值与计算值的比较Fig.7 Contrast calculated result with experimental result of flow stress（a）1020℃;（b）1050℃

3 结论

（1）随着温度的升高和应变速率的降低，Ti60合金流动应力显著减小，表现为较强的温度和应变速率敏感性。在不同的变形条件下，Ti60合金表现为不同的软化机制:高温、低应变速率条件下，流动应力很快达到稳态应力;低温、高应变速率条件下，流动应力经历了一段应变软化后，逐渐达到稳定状态。

（2）以幂函数型Arrhenius方程为基础，根据等温恒应变速率压缩试验数据建立了Ti60热加工过程本构关系。误差分析结果表明，试验温度条件下流动应力计算值与试验值之间的相对误差小于10%，因此本文建立的本构方程计算精度较高，能够比较精确地描述Ti60合金热加工过程中的流动行为。

［1］蔡建明，李臻熙，马济民，等.航空发动机用600℃高温钛合金的研究与发展［J］.材料导报，2005，19（1）:50-53.（CAI J M，LI Z X，MA J M，et al.Research and development of 600℃high temperature titanium alloys for aeroengine［J］.Materials Review，2005，19（1）:50-53.）［2］罗皎，李淼泉，潘洪泗，等.热变形条件对Ti60合金微

观组织的影响［J］.中国有色金属学报，2007，17（1）:53-58.

（LUO J，LI M Q，PAN H S，et al.Effects of deformation parameters on microstructure of Ti60 titanium alloy［J］.The Chinese Journal of Nonferrous Metals，2007，17（1）:53-58.）

［3］付艳艳，宋月清，惠松骁，等.航空用钛合金的研究与应用进展［J］.稀有金属，2006，30（6）:850-856.

（FU Y Y，SONG Y Q，HUI S X，et al.Research and application of typical aerospace titanium alloys［J］.Chinese Journal of Rare Metals，2006，30（6）:850-856.）

［4］聂蕾，李付国，方勇.TC4合金的新型本构关系［J］.航

空材料学报，2001，21（3）:13-18.

（NIE L，LI F G，FANG Y.New constitutive relationship for TI-6AL-4V alloy［J］.Journal of Aeronautical Materials，2001，21（3）:13-18.）

［5］ESTRIN Y.Dislocation-Density-Related Constitutive Modeling.Unified Constitutive Laws of Plastic Deformation［M］.New York:Academic Press，1996:69-106.

［6］MCQUEEN H J，YUE S，RYAN N D.Constitutive analysis in hot working［J］.Mater Sci Eng（A），2002，322（12）:43-46.

［7］ PHILIPPART I，RACK H J.High temperature dynamic yielding in metastable Ti-6.8Mo-4.5F-1.5Al［J］.Materials Science and Engineering（A），1998，243:196-200.

［8］SELLARS C M，et al.Hot workability［J］.Int Metallurg Rev 1972，17:1-24.

［9］MEDINA S F，HERNANDEZ C A.General expression of the Zener-Hollomon parameter as a function of chemical composition of low alloy and microalloyed［J］.Acta Mater，1996，44（1）:137-148.

［10］MILOVIC C，MANOJLOVIC D，ANDJELIC M，et al.Hot workability of M2 Type high-speed steel［J］.Steel Research.1992，63（2）:78-84