具有非局部反应项的非线性抛物方程解的整体存在性与爆破问题

严正香，胡洪安，李 煜

(1．信阳职业技术学院，河南 信阳464000;2．周口师范学院，河南周口466000;3．东南大学，江苏 南京211100)

本文研究来自于核反应动力学理论的非线性抛物微分-积分方程的整体解和爆破问题:

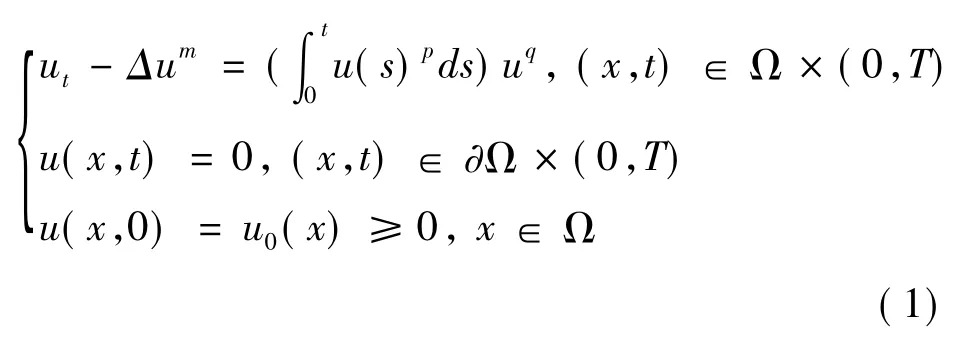
式中:m，p，q＞0;Ω为RN中的光滑有界区域．方程(1)虽然直接来自于核反应动力学理论，也可用来描述林学中的树木生长规律．

自然界中许多现象都可归结为非局部数学的问题．Bebernes和Bressan［1］研究了燃烧理论中可压气流的非局部反应扩散方程;Pao研究了由燃烧理论导出的非局部反应扩散方程．这些方程分为2类:一类是含有时间非局部积分源项的抛物方程;另一类是具有空空非局部积分源项的方程．第一类方程已经有了相当多的结果，例如:

式中:V(x)表示物理位势;|Ω|表示集合Ω的测度．此外，方程(2)源自于等离子体物理的Hartree-Fock理论;方程(3)描述了可压流理想气体的热反应特矾;方程(4)描述了某种化学晶格司的相互作用［1～4］．

王明新，王术和谢春红研究了下面非局部抛物方程组的临界指标问题:

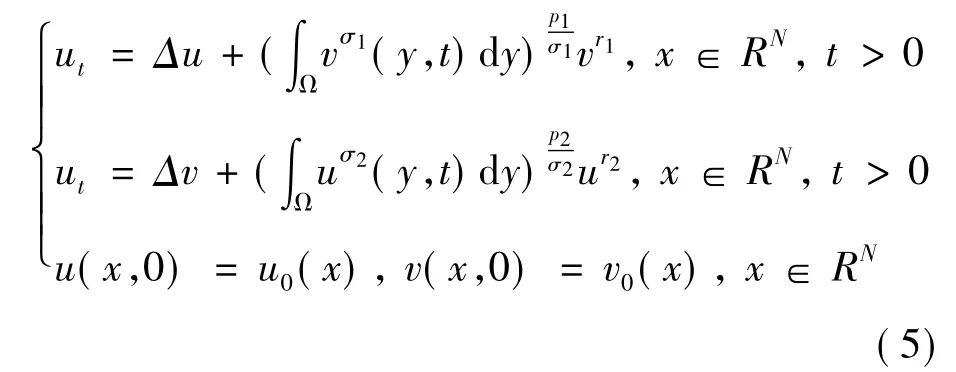
式中:pi≥ 0，σi，ri≥ 1，pi+ri＞ 1(i=1，2);u0(x)，v0(x) ≥ 0 及 u0(x)，v0(x) ∈ Lσ1(RN) ∩Lσ2(RN)∩L∞(RN)．他们得到了下面的结果:

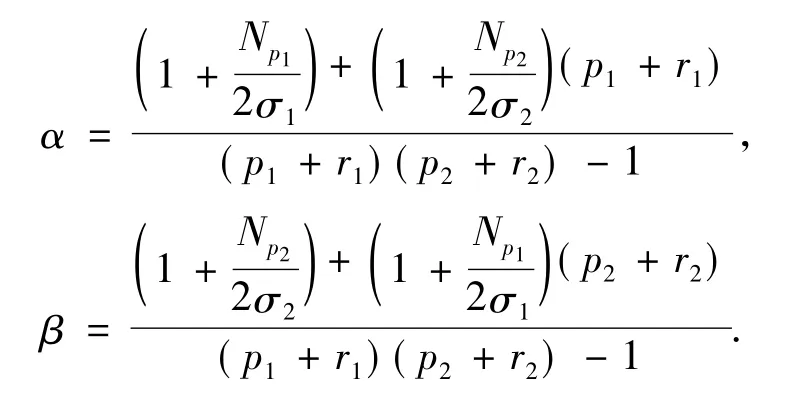
方程(1)在m=1，p，q ＞ 1的情形下，Daisuke Hirate［3］利用特征函数法和比较定理，证明了下面结果:

对于大初值，方程(1)的解在有限时间爆破，然而，对于小初值，存在整体解．

若u0(x)＞0(x∈Ω)，那么由经典的抛物方程理论，方程(1)存在唯一解 u(x，t)∈ C2，1(Ω ×(0，T))，u(x，t) ＞ 0．其中，T 是u(x，t)的最大存在时间．进而，若T＜∞，则，解u(x，t)在有限时间爆破，即

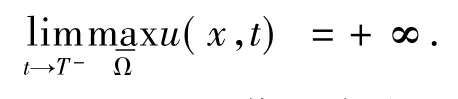
受Daisuke Hirata工作的启发，本文的目标是研究更一般的情形，结果如下:

(1)若0＜p+q≤1，那么方程(1)所有正解整体存在;

(2)当p+q＞1时，有3种情形如下:

(i)若m ＞p+q，则方程(1)所有正解都整体存在;

(ii)若0＜m≤1，则对于大初值方程(1)的解在有限时间爆破，然而，对于小初值，解整体存在;

(iii)若1＜m≤p+q，则方程(1)的解对于适当大的初值在有限时间爆破．

1 定理1的证明

首先，建立下面比较定理．

定理2 (比较定理) 令m ＞ 0，f，g:［0，∞) →［0，∞)是非减的一阶连续可微函数，若 u，v∈C2，1(Ω × (0，T)) ∩ C(×［0，T))，u(x，t) ＞ 0，v(x，t) ＞ 0，(x，t) ∈ (Ω × (0，T))，并满足:

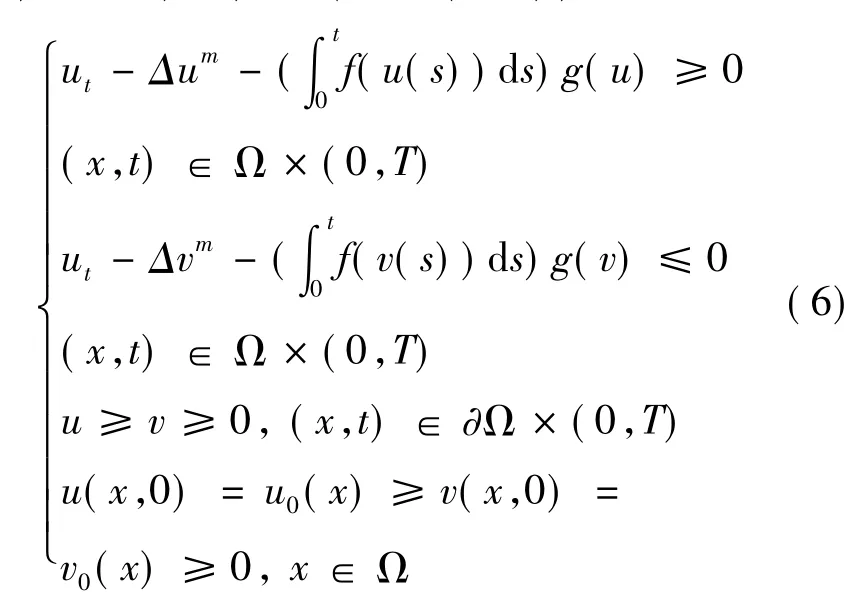
则 u(x，t) ≥ v(x，t)，∀(x，t) ∈ Ω × (0，T)．

证明 记w=u－v，由(6)，得

并设

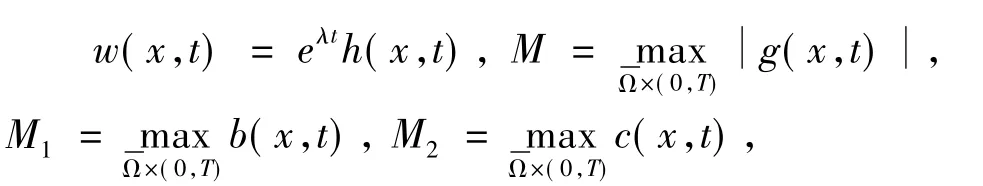
于是

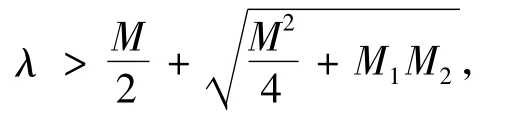
那么

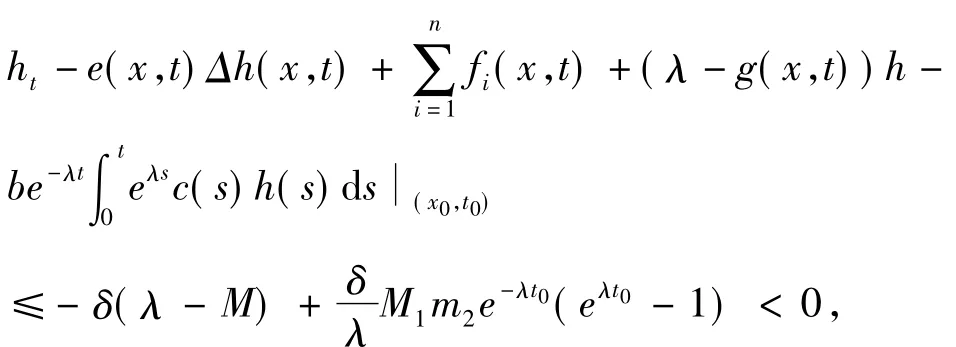
当 h(x，t) ≥ h(x0，t0)= － δ，而这与方程(7)的第一式矛盾，从而定理得证．

引理1 若u0(x)＞0(0∈Ω)且Δum0(x)≥0，那么 ut≥0．

证明 在方程式中令w=ut并利用上述比较定理不难证明该引理．

引理2 令u≥0，f(u)为一个局部Lipschitz连续函数且f(0)＞0，进而，如果f(u)为不减函数，当u＞0且d为Ω的半径．那么，当λ∈(0，λ*)时，边界值问题:

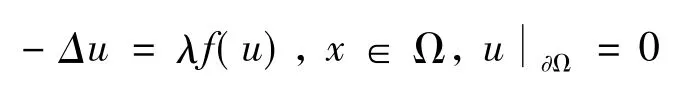
有一个非负解，其中λ*满足:

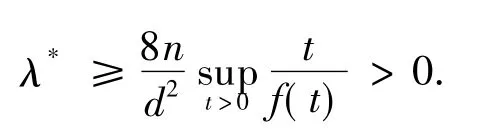
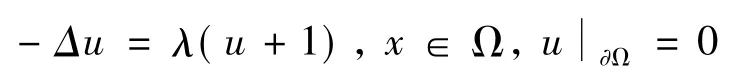
存在一个非负解ψ(x)．

定理1的证明将分以下几个引理完成．

引理3 若0＜p+q≤1，则问题(1)的所有正解整体存在．

证明 取

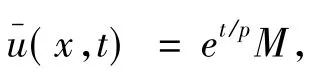
与 u－(x，0)=M ＞ u0(x)，x ∈ Ω，由比较定理不难得到该引理结论成立．

引理4 若p+q＞1且0＜m≤1，则方程(1)的解对于大初值在有限时间爆破，然而，对于小初值，解整体存在．

证明 取

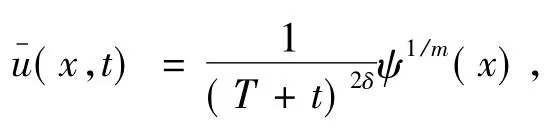
式中，δ=1/(p+q－m)，φ(x)由引理2确定．令C=，则0≤ ψ(x)≤C，T ＞ 1且T是不定常数．

若 2pδ＞ 0，则

此外，选取充分大的T ＞0．若2pδ=1，则

下面，证明方程(1)的解对于充分大的初值在有限时间爆破．首先，证明当m=1，p+q＞1时，上述结论成立．令φ(x)是下面问题的第一特征函数，这里，λ是第一特征值且φ(x)∈C2(Ω)∩C(Ω－)，φ(x) ＞ 0(x∈Ω)=1．在(1) 的2边同乘上φ(x)并在Ω上积分，再利用Höder不等式及引理1，得

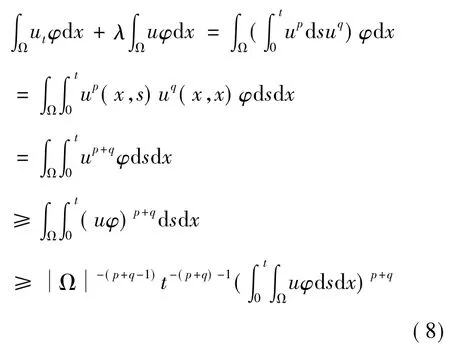
记

则，F(0)=0，F(t) ∈ C2(［0，T］)．再由(8) 可得下面微分不等式:

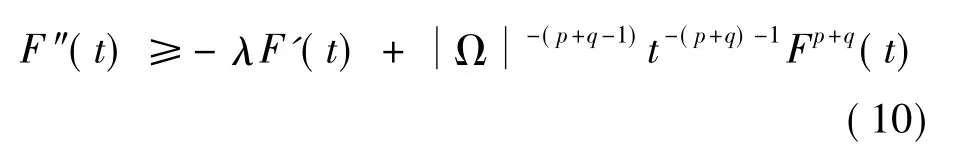
从(10)不难看出，对t≥T1＞0，存在T1＞0使得

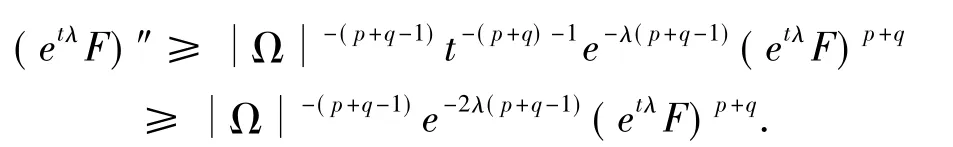
记 f(t)=etλF，若 t≥ T1＞ 0，则由上可得

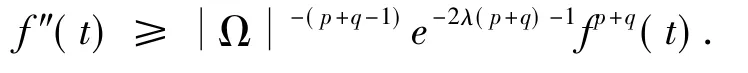
在上式2端同时乘上f'(t)并在(T1，t)上积分可得:当t≥T2≥T1时，存在T2＞0使得

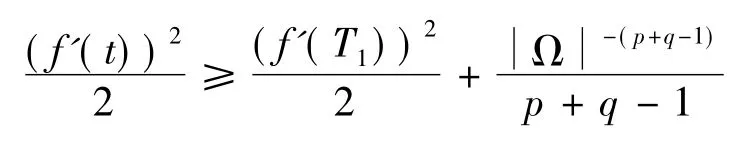
故，

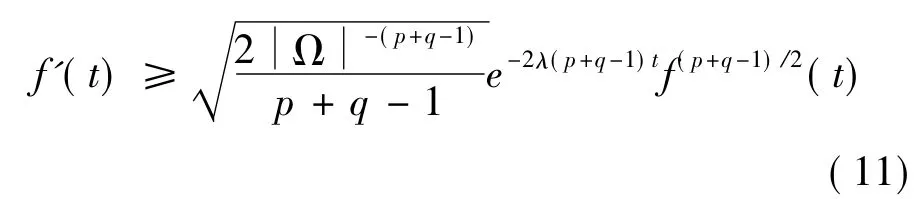
由(11)可得

这就说明，如果选取u0(x)充分大，则f(x)在有限时间爆破．

若0＜m ＜1，在方程(1)的2端同乘上φ(x)并在Ω上积分，借助于不等式

得

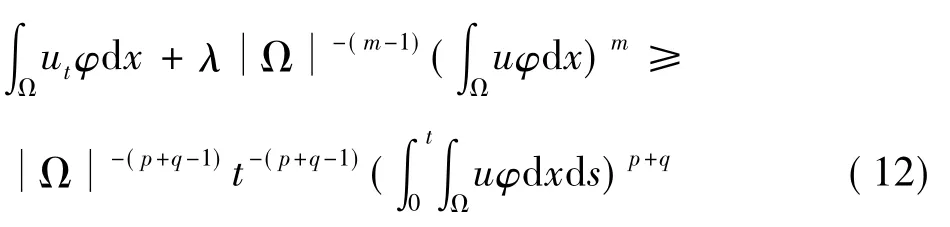
由引理1，取合适大的初值∫Ωu0φdx ≥1，则

再由(12)，得

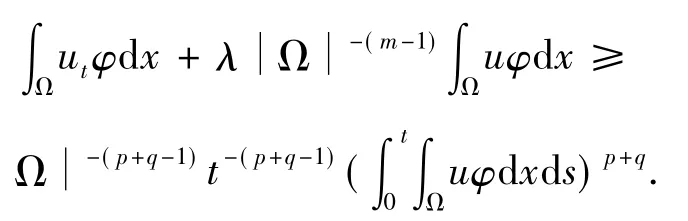
记

那么，类似的可得下面微分不等式

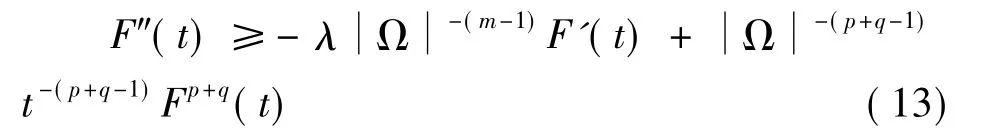
通过类似讨论不难发现u(x，t)在有限时间爆破，于是引理4得证．

引理5 若m ＞p+q＞1，那么方程(1)所有的正解整体存在．

证明 不难证明下面椭圆方程

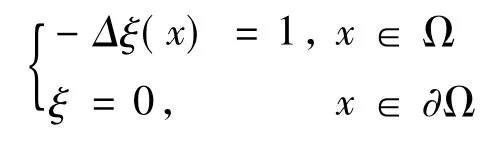
存在一个非负解ξ(x)，且0 ＜ ξ(x)≤N，x∈Ω，其中N为正常数．

取

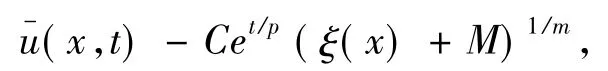
式中，C ≥ max{1，(N+M)1/(m－(p+q))}，那么

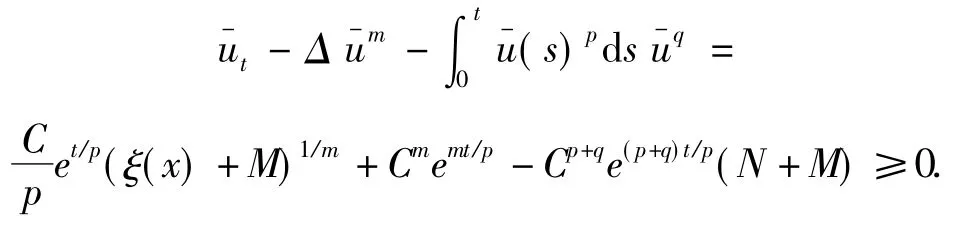
于是，引理5成立．

引理6 若1＜m≤p+q，则对于适当大的初值，方程(1)的解在有限时间爆破．

证明 在方程(1)2端同乘φm(x)并在Ω上积分有

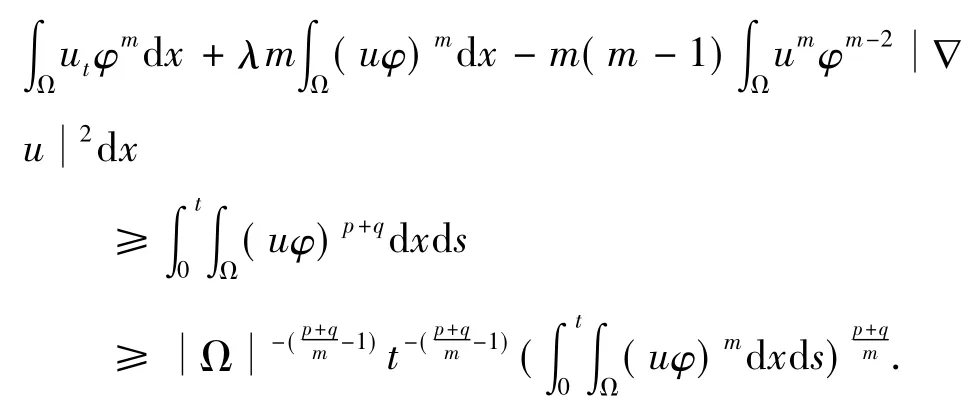
进而，

在(0，t)上积分上述不等式，得

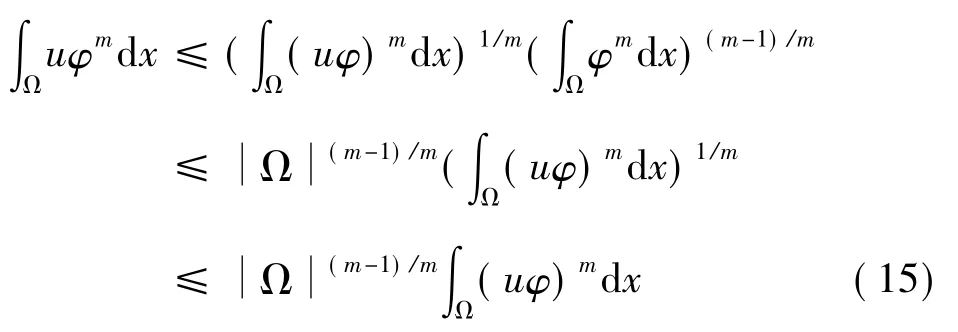
记

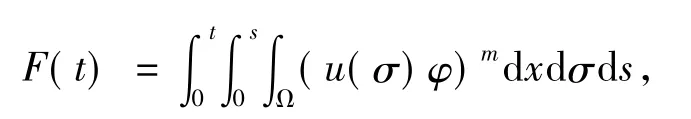
由(14)与(15)可得

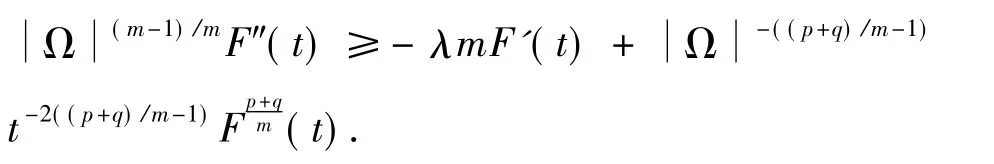
注意到

通过类似讨论可知，若取适当大初值时，解u(x，t)在有限时间爆破．

至此，由引理3与引理6以及上述讨论，完成了定理1的证明．

本文的结论对指导植树造林，防治病虫害有着重要的理论意义和广泛地应用前景．

［1］ BEBERNES J W，EBERLY．D．Mathematical problems from combustion theory ［M］． New York:Springer，1989．

［2］ FINA M．Boundedness of global solutions of nonlocal parabolic equations［J］．Nonlinear Anal，1997，30:855-877．

［3］ HIRATA D．Blow-up ror a class of semilinear integrodifferential equations of parabolic type［J］．Math．Meth Appl Sci，1999，22:1087-1100．

［4］ KAPLAN S．On the growth of solutions of quasilinear parabolic equations［J］．Comm Pure Appl Math，1963(16):305-330．

［5］ LEVINE H A．The role of critical exponents in blow-up theorems［J］．SLAM Review，1990，32(2):262-288．

［6］ WANG M X．Global solution，asymptotic behavior and blow-up problems for a lmdel of nuclear reaction［J］．Science In China(Series A)，1992，35(2):129-141．

［7］ 王明新．非线性抛物方程［M］．北京:科学出版社，1989．

［8］ WANG M X，WANG S，XIE C H．Critical Fujita exponents for nonlocal reaction diffusion sys-tems［J］．J Part Diff．Eqs，1999，12:201-212．

［9］ 叶其孝．反应扩散方程引论［M］．北京:科学出版社，1994．