基于Van Leer矢通量分裂的计算方法研究与应用

苏克勤，刘 英，曹殿立

(1．河南农业大学信息与管理科学学院，河南 郑州450002;2．河南大学，河南 开封475001)

在计算流体力学(CFD)中，构造能自动捕捉激波的算法一直是研究的重要内容．刻画粘性流动的N－S方程与刻画无粘流动的Euler方程相比，只多了具有线性形式的耗散项，由于耗散项所具有的椭圆型特征，其数值计算较为简单，所以，Euler方程的数值计算方法几乎可以直接应用到N－S方程的数值计算中，这也是CFD算法主要是围绕Euler方程不断发展的主要原因．Van Leer［1］构造出了一种以自己名字命名的上风格式——Van Leer矢通量分裂格式(FVS)．该格式是将通量矢量根据马赫数进行分裂，格式中的无粘矢通量的一阶导数在声速附近连续，避免了激波的产生．Van Leer FVS格式因其高效率，易于程序化运算等优点，常被其它算法所引用来更好地捕捉流场中的激波．1988年，在满足热力学第二定律给出的熵增原理的前提下，张涵信构造出了能自动捕捉激波、无波动、满足熵增条件的NND差分格式、并且该算法具有二阶精度，无自由参数．本研究将Van Leer FVS计算方法和NND差分格式相结合，提供了一种能有效捕捉激波、抑制数值解振荡的差分算法．该方法不仅具有Van Leer FVS方法的高效率和易于程序化运算等优点，并且有着NND差分格式较高的计算精度，能够自动捕捉流场中的激波．

1 二维Euler方程的Van Leer矢通量分裂

二维守恒型Euler方程为:

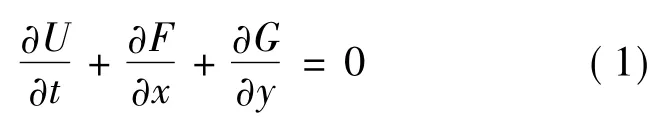
式中:

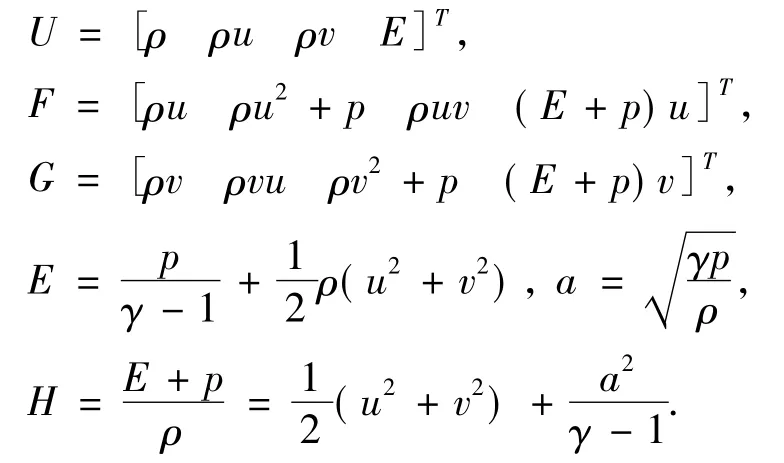
根据 Van Leer矢量分裂方法［1，3～6］，通量项可表示为:

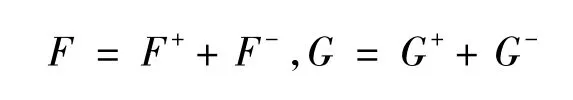
式中:

Van Leer FVS方法无矩阵运算，正负通量项的表达式固定，易于程序运算，具有较好的可操作性．该算法根据马赫数进行矢通量分裂，通量矢量的导数在声速附近的连续性避免了激波附近数值解振荡的产生，使得算法的精度和稳定性得到保证．

2 基于Van Leer矢通量分裂的新算法

NND格式是一种能自动捕捉激波的差分算法，物理背景明确．该算法可抑制奇偶失联振荡，因而得到了广泛应用［2，7，8］．对于方程组(1)，其 NND格式的显格式可以表示如下:

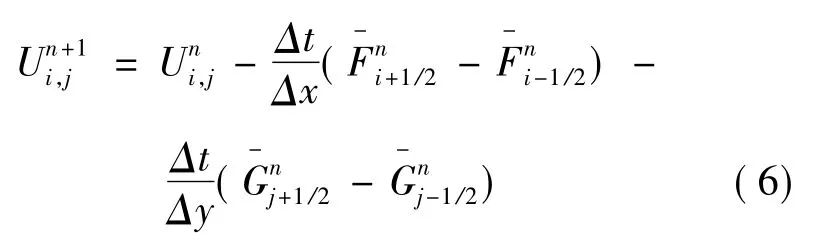
式中:

将Van Leer FVS方法中所得到的通量分解项(2)，(3)，(4)和(5)代入NND格式(6)中的通量分解项表达式，便构造出了一种新的差分算法．可以证明该算法空间上具有二阶精度，无需选择自由参数．

3 数值试验

出发方程为二维守恒型Euler方程(1)，取均匀流场．进口条件为:ρ=1．0，Ma=2．9，进气角β1=29°，p=1．0，γ =1．4; 出口条件为:

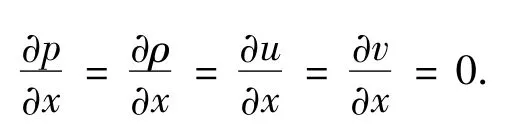
图1是数值试验得出的y=0．5时的压强分布，数据均经过无量纲化处理．由图1可知，结合Van Leer矢通量分裂和NND格式所构造的差分算法在该试验中有着较强的激波捕捉能力，避免了数值振荡的出现．

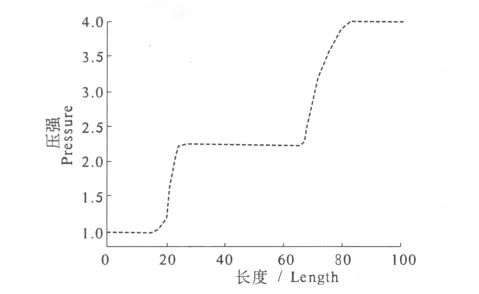
图1 y=0．5上的压强分布Fig．1 Distribution of pressure for y=0．5

4 结论

结合Van Leer矢通量分裂和NND格式，利用Van Leer FVS方法处理NND格式中的矢量通量分解项，构造出一种高效率的计算方法．通过对二维守恒型Euler方程的数值计算可以证明该差分算法能有效抑制激波附近数值解的振荡，有着较高的计算精度，保证了计算的稳定性．

［1］ VAN L B．Flux vector splitting for Euler equations［J］．Lecture Notes in Physics，1982，1970:507 －512．

［2］ 张涵信．无波动、无自由参数的耗散格式［J］．空气动力学报，1988(6):143－165．

［3］ VAN L B．Towards the ultimate conservative difference scheme I:the quest of monoticity［J］．Lecture Notes in Physics，1973，18:163 －168．

［4］ 阎 超．计算流体力学方法及应用［M］．北京:北京航空航天大学出版社，2006．

［5］ 张德良．计算流体力学教程［M］．北京:高等教育出版社，2010．

［6］ TORO E F．Riemann solvers and numerical methods for fluid dynamics［M］．New York:Springer，1999．

［7］ 张涵信．差分计算中激波上、下游出现波动的探讨［J］．空气动力学报，1984(2):12－19．

［8］ ZHANG H X，ZHUANG F G．NND schemes and their application to numerical simulation of two and three dimensional flows［J］．Advances in Applied Mechanics．1992(29):193－256．