机载通信互调干扰预估方法

朱孝政

（海军装备部 陕西 西安 710043）

机载通信设备间的干扰类型中互调干扰是较难抑制的一种干扰[1]，预估设备间的互调干扰量级是干扰抑制的首要工作。

本文首先建立了机载通信系统中互调干扰的分析模型，并采用矩量法结合微波二端口网络的方法求出模型中的参数，然后算出互调干扰的量级。

1 互调干扰分析模型

接收机互调主要由接收机前端非线性器件引起。接收机互调干扰的影响可用等效干扰电平来描述。通信接收机的等效互调干扰电平可用下式[2]表示：

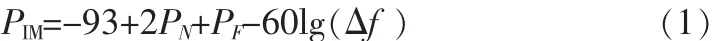
式中，PIM——接收机等效干扰电平（dBm）；PN——与接收机频率（fOR）较近的干扰信号（fN）在接收机输入端的干扰信号电平 （dBm）；PF——与接收机频率较远的干扰信号在接收机输入端的干扰信号电平 （dBm）；Δf——与接收机频率较近的干扰信号与fOR频率差归一于fOR的百分率。

当等效互调干扰电平PIM大于接收机灵敏度10 dB时则可以认为接收机被干扰。

计算无线设备间互调干扰模型如图1所示，其中P0为发射机发射功率，ηN1为网络端口的效率，ρ1为发射机天调至天线网络的驻波比，ηA1、ηA2为发射天线和接收天线效率，ηN2、ρ2为接收机的网络功率及驻波比。

图1 发射极对接收机的干扰电平计算步骤图Fig.1 Emitter of receiver interference level calculation step chart

2 天线间功率耦合计算

天线间的耦合度定义[2]为：

其中Pin为发射天线的净输入功率，Pout为接收天线的净输出功率。

应用矩量法进行分析时，任意划分的2个天线单元均满足端口网络的端口特性（电流连续），常常把加载段和激励段作为1个二端口网络，如图2所示，利用电路理论可以求得输入、输出端口的功率，进而可以得到天线间的耦合度[3]。

图2 天线单元等效二端口网络Fig.2 Antenna unit equivalent two terminal network

图3 SDT法散射体的分解Fig.3 SDT method scattering decomposition

上述耦合度模型中左端电流项需由矩量法求得，然而计算飞机这类电大尺寸目标时单纯应用矩量法计算量过大，因此空域分解技术。空域分解技术[4]（Spatial Decomposition Technique-SDT）基本思想是将大的散射体分解为小的散射体分别计算如图3所示，可以在计算存储量和计算速度上大大改善矩量法。空域分解技术假设原散射体由多个子散射体组成，电流分布于散射体表面，将散射体表面分解为M个子域，先求得每个子域上的电流分布，然后总的散射场由每个子域上的电流的散射场叠加得到。空域分解法的积分方程表达式为：

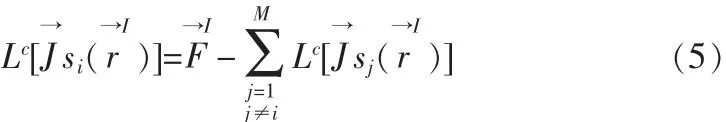
方程（5）中，左边代表待求子域上的电流的积分（子域电流的散射场），右端第一项代表入射源，右端第2项是关于其他子域的电流积分之和，代表这些子域上的电流所产生的散射场的总场，左端的电流是待求量，可以通过迭代过程求得，具体过程是：当i=1时，右端的入射源项是已知的，其他子域上的电流可以先由物理光学法求得近似解，再求得这些电流的散射场（即右端第2项），代入方程右端可以求得子域S1上的电流近似解当i=2时，S1上的电流已经由第一步求得，S3～SM上的电流仍然由物理光学法求得，将 S1、S3～SM上电流的散射场代入方程右端，可以得到子域S2上的电流近似解依此类推，可以求得各个子域上的电流（i=1～M）。这是第1轮迭代，第2轮迭代时，方程右端第2项的所有电流均采用第一轮迭代的结果，继续求解第p+1轮迭代时，采用第p轮所求得的电流求解持续这一过程，一直到每个子域上的电流值不再有变化或前后2次迭代每个子域上的电流值的误差不大于1个给定的收敛参数ε为止。

3 数值结果

某型飞机上共上装4部通信电台，文中将采用实测结果作为验证上述方法的标准，而在对电台进行实际测试过程中只检测到了三阶-Ⅰ型互调（由2个信号产生），故本文只仿真了三阶-Ⅰ型互调量，以便与实测数据相比较。

计算实例1：电台1小功率发射，发射频率为75 MHz；电台3中功率发射，发射频率为240 MHz，电台2处于接收状态。该组合形式下，互调产物的频率落入接收电台接收带内的只有90 MHz和390 MHz 2种，其仿真与实测结果如表1所示。

表1 计算实例1仿真与测试结果对比Tab.1 Calculating examples of 1 simulation and comparison of the test results

计算实例2：电台1小功率发射，发射频率为60 MHz；电台2中功率发射，发射频率为220 MHz，电台4处于接收状态。该组合形式下，互调产物的频率落入接收电台接收带内的只有100 MHz和340 MHz 2种，其仿真与实测结果如表2所示。

表2 计算实例2仿真与测试结果对比Tab.2 Calculating examples of 2 simulation and comparison of the test results

计算实例3：电台2中功率发射，发射频率为55 MHz；电台3中功率发射，发射频率为60 MHz，电台1处于接收状态。该组合形式下，互调产物的频率落入接收电台接收带内的只有50 MHz，其仿真与实测结果如表3所示。

表3 计算实例3仿真与测试结果对比Tab.3 Calculating examples of 3 simulation and comparison of the test results

从上述对比实例可以看到，仿真结果与实测结果吻合的较好，误差仅为2 dB，证明了本文方法的有效性。

4 结 论

文中建立了无线设备间互调干扰量的仿真计算模型，并应用区域分解矩量法对机载通信系统设计中的互调干扰问题进行了计算分析，仿真结果与实测结果吻合良好。数值仿真结果证明本文方法可作为实际工程的有力设计工具。

[1]刘晓娟.基于单片机的数控恒流源设计[J].哈尔滨师范大学自然科学学报，2008，24（6）：39.

LIU Xiao-juan.The design of digital control-constant current based on microcontroller[J].Natural Science Journal of Harbin Normal University，2008，24（6）：39.

[2]陈穷.电磁兼容性工程设计手册[M].北京：国防工业出版社，1993.

[3]习俊梅，朱杰斌，黄良兵，等.便携式数字化超声检测仪[J].仪表技术与传感器，2007（9）：18-19.

XI Jun-mei，ZHU Jie-bin，HUANG Liang-bing，et al.The portable digital ultrasonic testing device[J].Instrument Technique and Sensor，2007（9）：18-19.

[4]秦曾煌.电工学[M].北京：高等教育出版社，2004.

[5]李会兵.基于虚拟仪器的直升机电动执行机构检测仪的研制[D].西安：西安科技大学，2005.

[6]任哲.嵌入式实时操作系统μC/OS-II原理与应用[M].北京：北京航空航天大学出版社，2005.