粗糙集理论在学生综合评价中的应用研究

沈泽刚，钟德春

（渤海大学 信息科学与技术学院，辽宁 锦州 121000）

培养综合素质是人才培养的核心内容。实行综合素质评价，是深化课程改革、全面实施素质教育的重要措施。遵照《教育部关于积极推进中小学评价与考试制度改革的通知》精神，全国各地积极探索，取得了中学生综合素质评价的有益经验。但是，由于学生素质综合评价是一项复杂的工作，是一类带有大量不确定因素的半结构化或非结构化问题。因此，在评价实施过程中存在一些突出问题，特别是评价手段滞后，缺乏操作性、可行性，导致评价效果不佳[1]。为了改善现有综合评价方法的不足[2]，本文提出了一种基于粗糙集理论的学生素质综合评价方法。首先介绍了粗糙集信息系统和属性约简的概念，然后提出基于粗糙集理论学生综合评价的一般过程，进而实现综合评价系统的指标约简和权重设置。以弥补评价方法中主观性和片面性的问题，并且能够有效地减少综合评价问题的计算量。最后，通过例子分析，验证了该方法的可行性和实用性。

1 粗糙集理论及其基本概念

粗糙集理论[3-4]由波兰科学家Z.Pawlak于1982年提出，它是继概率论、模糊集、证据理论之后又一个刻画不完整性和不确定性的数学工具，能处理定性、定量因素，有效分析不精确、不一致、不完整等各种不完备信息；能对数据进行分析和推理，发现数据中隐含的规律。经过30多年的发展，粗糙集理论已成功地在数据的决策与分析、模式识别、机器学习与知识发现等领域得到广泛应用[5]。

1.1 信息系统

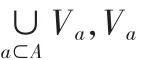
1.2 知识约简

定义 2 设S=（U，A，V，f）， 是一个信息系统，a∈A， 如果ind（A-{a}）=ind（A）， 则称a在A中是不必要的；否则称a在A中是必要的。不必要的属性在信息系统中是多余的，如果将它从信息系统中删除，不会改变信息系统的分类能力，相反，若从信息系统中删除一个必要的属性，则一定改变信息系统的分类能力。

定义 3 设 S=（U，A，V，f），是一个信息系统，如果 a∈A 在 A中都是必要的，则称属性集A是独立的；否则称A是相关的。对于相关的属性集来说，其中包含有多余属性，可以对其约简。

定义 4 设 S=（U，A，V，f）， 是一个信息系统，A 中所有必要的属性组成的集合称为属性集A的核，记为core（A）。

定义 5 设 S=（U，A，V，f），是一个信息系统，P⊆A，如果 P是独立的，且 ind（P）=ind（A），则称 P是 A 的一个约简。

1.3 信息系统属性的重要性度量

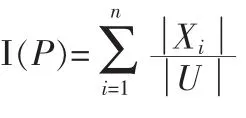
定义 7 设 S=（U，A，V，f），是一个信息系统，属性 a∈A 在A 中的重要性定义为：SGF（A-{a}）=I（A）-I（A-{a}）。 上述定义表明属性a∈A在A中的重要性是由A中去掉{a}后所引起的信息量变化的大小来度量的。

2 基于粗糙集理论综合评价的一般过程

构建基于粗糙集理论的综合评价过程[6]如图1所示。

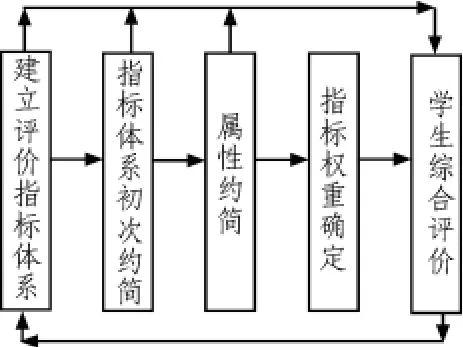
图1 基于粗糙集理论的综合评价一般过程Fig.1 The general process of comprehensive evaluation based on Rough set theory

2.1 建立评价的信息系统

利用综合评价的指标体系中所有最低级指标作为信息系统的属性集合，要进行综合评价的对象作为系统中的对象集合，在评价中对每一个最低级指标项目的评价结果即每个属性值用“优”、“良”、“一般”和“差”4个等级或其他离散化地等级来衡量，并且分别用相应的数值来代替，因为粗糙集理论只能处理离散化的数据，若不是离散化的数据，需通过一定的离散化方法，将数据转化为离散化的，继而构建信息系统。

2.2 信息系统约简

观察信息系统 S=（U，A，V，f），对于论域 U，若属性 i，j∈A对应的评价对象的属性值相同，则认为属性i，j具有相同的分辨能力，只需保留一个。根据约简和核的概念，计算不可分辩关系，求解信息系统的核和各种约简。

2.3 权重的确定

定义 8 设 S=（U，A，V，f），是一个信息系统，A={a1，a2，…，am}，属性 ai∈A 在 A 中的重要性为 SGFA-{a}（ai），则 ai∈A 的权重定义为：

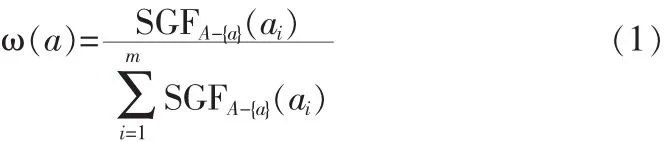
由定义8式（1），先计算底层各指标权重，然后计算更高一层各指标的权重，依此类推。

2.4 学生综合评价

根据每个对象在信息系统中的初始得分情况，利用加权综合评分公式：

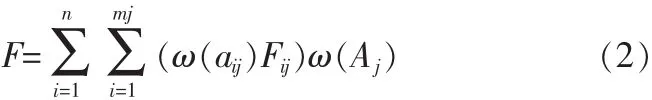
计算每个对象最终得分，其中 ω（Aj）和 ω（aij）分别为信息系统约简后的每个一级指标和二级指标权重；n和mj分别为信息系统约简后的一级指标和二指标的个数；Fij为该对象在属性aij下的取值。最后按照各指标值的大小，对评价对象进行比较分析。

3 粗糙集理论在学生综合评价的应用

3.1 建立高中学生综合评价信息系统

以《辽宁省普通高中学生综合素质评价方案（试行）》的通知为核心，建立学生综合评价指标体系，一级指标有：道德品质（A1），公民素养（A2），学习能力（A3），交流与合作（A4），运动与健康（A5），审美与表现（A6）；二级指标有：是非观（A11），亲社会（A12），诚实守信（A13），热爱国家（A21），社会责任（A22），遵纪守法（A23），文明习惯（A24），学习态度（A31），学习兴趣（A32），学习习惯（A44），创新意识（A34），表达能力（A41），倾听习惯（A42），评价能力（A43），生活方式 （A51），体能（A52），情绪（A53），意志（A54），感受美（A61），表达美（A62）。

以某班的所有学生作为评价对象， 记为：U={u1，u2，u3，…}，评价结果的“优”、“良”、“中”和“差”用 4，3，2，1 数值来代替，从而构成一个信息系统。部分同学的数据如表1所示。

表1 学生综合评价的初始信息系统Tab.1 The original information system of students’comprehensive evaluation

其中学生个体 U={u1，u2，u3，…}，属性集 A={A1，A2，A3，A4，A5}={{A11，A12，A13}，{A21，A22，A23，A24}，{A31，A32，A33，A34}，{A41，A42，A43}，{A51，A52，A53，A54}，{A61，A62}}，值域 V={1，2，3，4}。

3.2 综合评价指标体系的初次约简

观察信息系统 S=（U，A，V，f），对于论域 U，若属性 i， j∈A对应的评价对象的属性值相同，则认为属性i，j具有相同的分辨能力，只需保留一个。初次约简后，得到的指标体系，如表2所示。

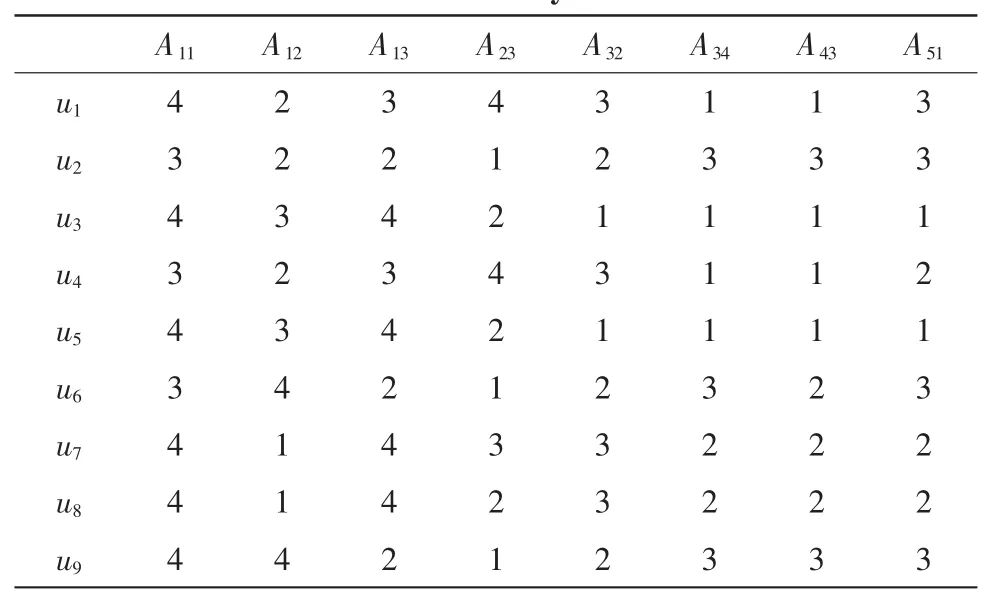
表2 学生综合评价初次约简的信息系统Tab.2 Students’comprehensive evaluation first reduction information system

3.3 属性约简

根据不可分辨关系可得：

U/ind{A}=U/ind{A-{A11}}=U/ind{A-{A12}}=U/ind{A-{A13}}=U/ind{A-{A32}}

=U/ind{A-{A43}}=U/ind{A-{A51}}={{u1}，{u2}，{u3}，{u4}，{u5}，{u6}，{u7}，{u8}，{u9}}；U/ind{A-{A23}}={{u1}，{u2}，{u3}，{u4}，{u5}，{u6}，{u7，u8}，{u9}}；U/ind{A-{A34}}={{u1}，{u2}，{u3，u5}，{u4}，{u6}，{u7}，{u8}，{u9}}，有属性：{A11}，{A12}，{A13}，{A32}，{A43}，{A51}是不必要的，则属性：{A23}，{A34}是必要的，即信息系统的核为：core（A）={A23，A34}，因此存在 6 个约简为：A1={A23，A34，A11}；A2={A23，A34，A12}；A3={A23，A34，A13}；A4={A23，A34，A32}；A5={A23，A34，A43}；A6={A23，A34，A51}。 下边以 A1={A23，A34，A11}为例进行演算，则表2可进一步约简为表3，即属性约简后的信息系统：

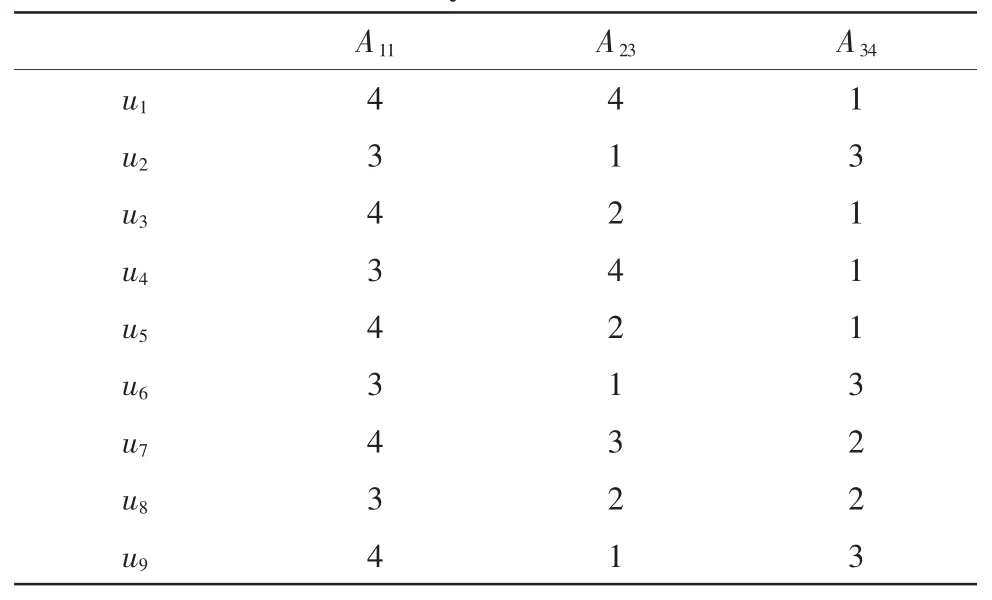
表3 属性约简后的信息系统Tab.3 Information system of attribute reduction

通过属性约简，把冗余的属性删除了，约简后的信息系统与原信息系统具有相同的分辨能力，即具有相同的决策作用,通过属性约简后的信息系统属性比较少，简化了综合评价指标集，增强了综合评价的可操作性，对评价的效率有一定提高。同时，也看到看到我们当前的教育在学生的创新意识和知法、懂法、守法、用法方面还存在着不足，对我们今后的教育工作也有一定的指导性作用。

3.4 对象综合评价

根据式（2）和定义6，7，8，可得各对象的综合评价值分别为：3.548，2.662，2.948，3.348，2.525，3.640，2.633，2.496，3.440。

上述综合评价结果是对学生综合发展情况的客观真实反映，不受人的主观性影响，也提高了评价过程的效率。

4 结束语

文中引入基于粗糙集理论的属性约简和属性重要性度量方法对学生进行综合评价，可以对有限的指标数据进行有效挖掘，无须先验数据，简化指标体系，也可以客观地计算指标重要性。该方法弥补其它评价方法[2]中主观性和片面性的问题，并且能够有效地减少综合评价问题的计算量,提高评价过程的效率。同时,在进行实例验证时，发现了限制学生综合发展的因素有创新意识和法律意识。但是，由于实例验证的对象有限，并不能完全代表各地中学生的综合发展状况。

[1]蔡敏.高中学生综合素质评价：现状、问题与对策教育科学[J].教育科学，2011（2）：67-71.

CAI Min.Evaluation of comprehensive qualities of high school students：current situation， problems and countermeasures[J].Education Science，2011（2）：67-71.

[2]黄光明，张巍.基于Rough Set的综合评价方法研究[J].计算机工程与应用，2004（2）：36-38

HUANGGuang-ming，ZHANGWei.Researchoncomprehensive measurementmethod based on rough set[J].Computer Engineering and Applications，2004（2）：36-38.

[3]Pawlak Z.Rough sets theoretical aspects of reasoning about data[M].Boston：Kluwer Academic Publishers，1991.

[4]Pawlak Z.Rough set theory and its applications to data analysis [J].Cybernetics and Systems：An International Journal，1998，29（1）：661-688.

[5]张文修，吴伟志，粱吉业.粗糙集理论和方法[M].北京：科学出版社，2001.

[6]钟嘉鸣，李订芳.基于粗糙集的CAI课件综合评价模型[J].计算机工程与应用，2008，44（22）：213-225.

ZHONG Jia-ming，LI Ding-fang.Research on comprehensive measurement method of CAI course ware based on rough set[J].Computer Engineering and Applications，2008，44（22）：213-225.

[7]李健，赵世慧，叶娜.基于B/S架构的信息系统网页重入问题研究[J].陕西电力,2010（09）：50-52。

LI Jian，ZHAO Shi-hui，YE Na.Probe into reentrant Web pages in information system based on B/S frame[J].Shaanxi Electric Power，2010（9）：50-52.