高斯噪声源电路的设计与实现
吴 帆,李会方
(西北工业大学 陕西 西安 710129)
在硬件实现的跟踪系统中,经常需要高斯噪声信号源来提供噪声。传统的高斯噪声大多在基于DSP的软件系统上生成,其产生速度比硬件系统工作频率要慢很多,且不利于SOC(system on chip)的集成。通常,在这样的系统里有大量的运算与逻辑操作(例如,硬件粒子滤波系统),高斯源作为噪声模块只是很小的一个功能块,因此设计时需要尽量减少噪声源占用的资源,以便将有限的FPGA的资源尽量留给其他计算模块[1]。然而,噪声的精度却对最终的跟踪结果精度有着直接影响,因此要想获得高精度的跟踪结果必须改善噪声的精度。为了获得占用资源少、精度高的高斯噪声源电路,设计了本文的高斯噪声产生方案。该方案由Verilog HDL编程,可移植性强,可作为功能模块移植到其他系统中产生高斯噪声。
1 方案选择
为了获得高斯噪声,通常采用数字合成方法[2],首先产生均匀分布的伪随机数噪声,然后通过一定的转换方法获得高斯白噪声。
均匀分布的伪随机数产生已经有较长的研究历史,主要的方法有:线性同余法、m序列产生法、logist 方程法、进位加方法[3]。FPGA具有并行计算的优势,可以胜任基本逻辑、简单加减法、大小比较、多路选择和时序逻辑等操作。通常FPGA采用查找表实现组合逻辑运算,当组合逻辑过于复杂时,往往需要使用多级查找表来完成运算,大大降低速度,如乘除法[4]。因此用FPGA实现伪随机数发生器,算法应该尽量简单,并尽量不要使用乘除法。考虑到以上因素,本设计采用m序列产生法,该算法具有简单、产生速度快、可重复性强的特点,并且得到的伪随机序列周期较长。将均匀分布的随机序列转化为高斯分布的随机序列的方法主要有函数变换法、中心极限法、查找表法3种[5]。前两种方法都使用到了复杂的运算,在FPGA上实现时需要占用较多的逻辑资源。查找表法通过图1所示的均匀噪声和高斯噪声之间的映射关系建立查找表,通过查表方法得到对应高斯噪声。若对每个均匀输入都建立查找关系,则对于n位的均匀噪声输入需要建立2n大小的查找表,查找表大小随着输入位数增加成指数增长。当为了增加精度而提高n时,查找表大小迅速增长到不能接受。文献[2]利用折线来逼近映射曲线,查找表里存储折线的偏移和斜率,从而减少查找表的大小。观察图1发现曲线在高斯噪声绝对值小的地方斜率小,在绝对值大的地方斜率大。如果采用均匀量化的方法,则在高斯噪声绝对值越大的地方精度越差。要想得到更高精度,就要增加均匀量化级数,增大查找表[6]。文中引入非均匀划分的思想,在斜率较小的地方,用较少的折线逼近映射曲线,在斜率大的地方,用更多的折线逼近映射曲线,这样可以在不增加查找表大小的情况下改善精度。
文中的安排如下:在第2节中给出了均匀伪随机数的实现过程。第3节详细描述了本文的非均匀划分的方法和寻址方式。在最后1节,给出了设计结果和结论。

图 1 (0,1)均匀分布与(0,1)高斯分布的映射关系Fig.1 Mapping relationship between (0,1) uniform distribution and(0,1) Gaussian distribution
2 均匀分布伪随机数产生
m序列是最长线性反馈移位寄存器的简称[7],它是由带线性反馈的移位寄存器 (Linear Feedback Shift Register,LFSR)产生的周期最长的序列。m序列的每个状态可以看成对应一个随机噪声,当m序列使用n级寄存器时,对应的均匀噪声的重复周期最大为2n-1。为了生成m序列,需要选择合适的反馈节点使得输出序列最长。反馈节点的选择决定了输出序列的周期。例如:对于一个3位宽的LFSR,如果选择节点 [1,2],输出将在2个值间循环。相比,如果选择节点[0,2],输出值的周期可以达到23-1个。表1给出了不同位宽时的LFSR达到最大周期时节点的选择。
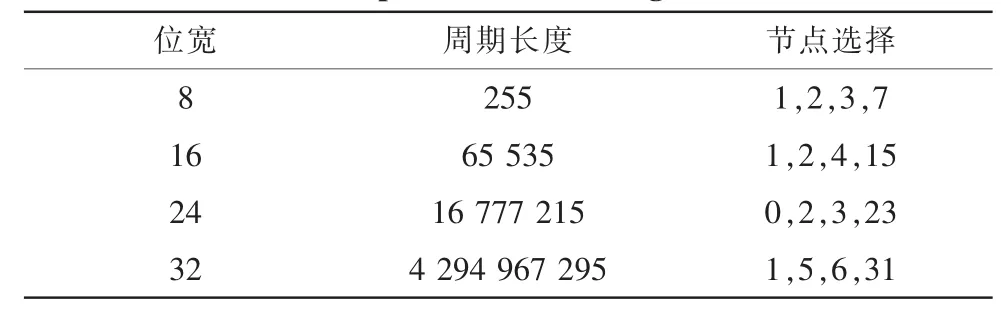
表1 最长周期的LFSR的节点选择Tab.1 Taps for maximal length LFSRs
对于采用异或门作为反馈的LFSR,当进入所有位状态为逻辑0时,输出将阻滞在全0状态。为了避免在电路进入这种全0状态,我们对常规的LFSR电路稍微做了一点改进,使得当电路进入全0时,将自动跳转到合法状态继续运行。图2以n等于8为例给出了本人LFSR的电路。

图2 8位的LFSR实现电路Fig.2 Implementation circuit for 8 bits LFSR
从m序列的实现过程来看,相邻的两个输出值间相关性很强,这必然影响到均匀噪声信号的独立性,为了减少这种相关性,可以采取L个LFSR并行工作,分别给予每个LFSR不同的初始种子,再从L个输出中抽取一个作为均匀噪声序列的输出。参考文献[5],选择LFSR的位宽n=32,并行运行L=6个LFSR来产生均匀分布噪声序列。
3 高斯噪声产生方
图1的映射关系可以用函数表示为:

式中x为均匀随机变量,y为高斯随机变量。随着高斯噪声y的绝对值增大,用来逼近曲线的直线的斜率也增大,若使用均匀分段的折线来逼近映射曲线,则高斯噪声绝对值越大的地方,用来逼近映射曲线的斜率越大,由于逼近所带来的误差越大。因此,使用非均匀划分的方法,在高斯噪声绝对值小的地方采用更少的直线来逼近,相反,在高斯噪声绝对值大的地方,采用更多的直线来逼近,这样在逼近直线总数不变的情况下,改善噪声的精度。同时,均匀噪声与高斯噪声之间的映射关系曲线关于点 (0.5,0)对称,因此只考虑横坐标位于(0.5,1)的情形,从而节约一半的存储空间。对于横坐标位于(0,0.5)的情况,可以通过适当转换获得。以8位的输入为例来解释本文的非均匀划分方法和寻址方式。首先,选择1-2-n(1≤n≤8)作为边界点来划分曲线,总共划分为7段,每一段对应一个存储空间,如图3所示。
为了对这7段空间进行寻址,设计图4的寻址电路,该寻址电路具有收缩的特性[8],随着地址增长,2个相邻地址对应的输入x间的距离越来越小。当x7=1时,对应x坐标大于0.5,寻址电路中间部分可以视为通路,电路直接寻址取得直线斜率和偏移后通过计算模块获得高斯噪声输出。当x7=0时,通过多路选择器对寻址做相应变换,同时x7作为控制信号,控制计算模块结果取反。
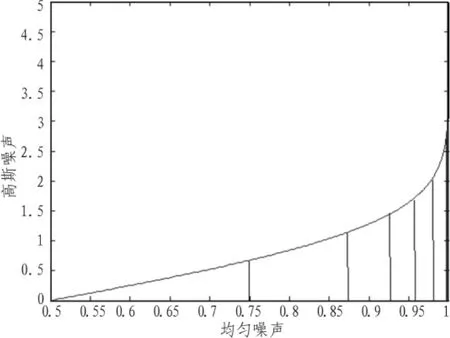
图3 映射曲线非均匀分区示意图Fig.3 Diagram of nonuniform partition to mapping curve

图4 寻址电路Fig.4 Addressing circuit
4 仿真结果
文中采用XILINX公司的Virtex5系列的XC5VLX50T芯片上实现了上述设计,设计主要占用了2%的可配置的SLICE和一块片上 BRAM,实现了±4σ的高斯噪声源,将5 000点的输出结果导入到Matlab里并绘制直方图,得到如图5所示。
由图可以看出,生成的噪声序列密度函数基本符合高斯分布,达到了设计要求。
5 结束语
高斯源噪声作为最常用的噪声源之一,经常被应用于各种需要加噪处理的系统和算法。相对于传统的高斯噪声源来说,基于FPGA的非均匀折线逼近的高斯噪声源具有高速、占用资源少、精度高、可移植性强的优点。容易作为IP核,移植到高速的数字系统中。

图5 输出噪声序列直方图Fig.5 Histogram of the output noise sequence
[1]Vasilescu G.Electrocnic noise and interfering signals:principles and applications[M].Berlin:Springer-Verlag,2005.
[2]艾余雄,寇艳红.一种基于FPGA的高斯白噪声发生器的设计与实现[J].遥测遥控,2009,30(6):36-40.
AI Yu-xiong,KOU Yan-hong.Design and implementation of a FPGA-based Gauss noise generator[J].Journal of Telemetry,Tracking and Command,2009,30(6):36-40.
[3]刘正高.标准均匀随机数的产生方法分析 [J].航天标准化,1996,13(5):11-13.
LIU Zheng-gao.Standard uniform random number generation method analysis[J].Standardization of Aerospace,1996,13(5):11-13.
[4]Wolf W.FPGA-based system design[M].Princeton:Prentice Hall PTR,2004.
[5]王林,芮国胜,田文飚.基于FPGA的高斯白噪声生成[J].现代电子技术,2011,34(3):104-106.
WANG Lin,RUI Guo-sheng,TIAN Wen-biao.Gaussian white noise generating based on FPGA[J].Modern Electronics Technique,2011,34(3):104-106.
[6]汪春霆,李修国,王爱华.基于FPGA的高精度高斯白噪声产生方法[J].北京理工大学学报,2010,30(4):474-477.
WANG Chun-ting,LI Xiu-guo,WANG Ai-hua.Method to generatehigh-preciseGaussiannoisebasedonFPGA[J].Transactions of Beijing Institute of Technology,2010,30(4):474-477.
[7]Lee D U,Wayne L,Villasenor J D,et al.A hardware Gaussian noise generator using the Box-Muller method and its error analysis[J].IEEE Trans.on Computers,2006,55(6):659-671.
[8]Lee D U,Wayne L,Villasenor J D,et al.A hardware Gaussian noise generator using the Wallace method[J].IEEE Trans.on Very Large Scale Integration (VLSI) systems,2005,13(8):911-920.

