气体压力对气流冲击平板换热特性的影响研究
韩雅慧
(北京航空航天大学 航空科学与工程学院,北京 100191)
0 引言
在飞行器飞行过程中,舱内压力随着气体的泄露逐渐降低,并最终达到0.3atm。在通风体积流量不变条件下,随着舱内压力降低,设备通风换热特性会持续恶化。由于以往这方面的研究很少,设备通风换热特性随气压变化的规律不太清楚,这给通风系统设计造成了一定的困难。本文将模拟在不同压力条件下气流冲击平板对换热特性影响的研究,为舱内设备的通风系统设计提供一定的理论依据。
1 数学物理模型
1.1 物理模型
计算平板由保温材料和铝板组成,如图1所示。舱内设备表面会有垂直来流方向和平行来流方向两种情况,换热状态有三种,如图2所示。
计算中把平板置于2000×660×900的风道中,风道气流入口速度为0.3m/s,温度为25℃,铝板发热功率5.3W。
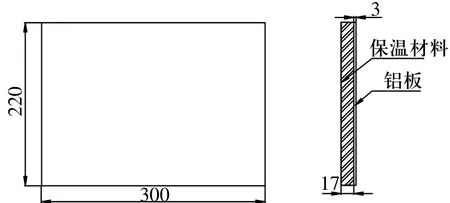
图1 平板尺寸示意图
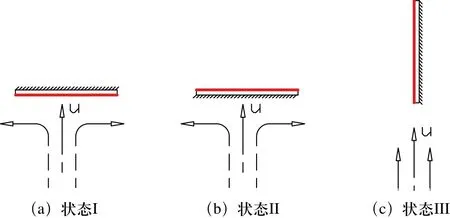
图2 计算三种工况
1.2 数学模型
1.2.1 控制方程
本文采用求解N-S方程和能量方程的方法模拟了气流冲击平板时的温度分布。假定空气为理想气体,在稳态情况下,描写平板周围空气换热过程的控制方程在直角坐标下为[2]:
质量守恒方程:
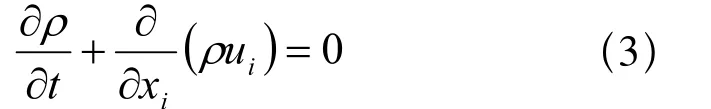
动量守恒方程:

流体区域的能量守恒方程:
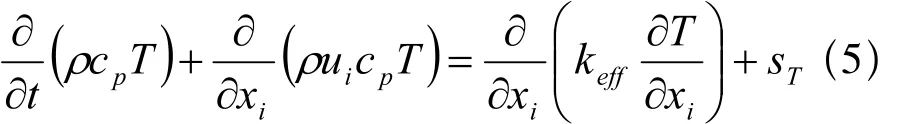
固体区域的能量守恒方程:
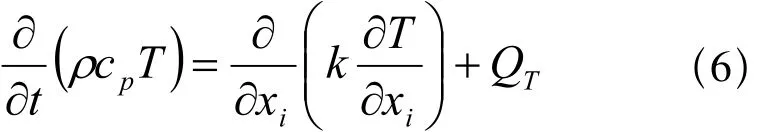
其中,keff= k+kt有效导热系数;k为分子导热系数;kt=cpPrt湍流导热系数;St为能量方程源项;Q为体热源;湍流粘性系数,由湍流模型给出。
1.2.2 边界条件和计算网格
对平板温度场进行数值模拟时,边界条件包括速度边界和温度边界。速度边界:通道入口速度为0.3m/s;固体表面为无滑移边界条件。温度边界:发热铝板表面给定热流密度 ,气流与壁面之间的传热采用壁面函数法处理。计算网格如图3所示。
图3 气流冲刷平板计算网格示意图
2 结果与分析
2.1 经验公式
气流方向与平板平行时,相应平板的的对流换热系数计算公式可以描述如下[1]:
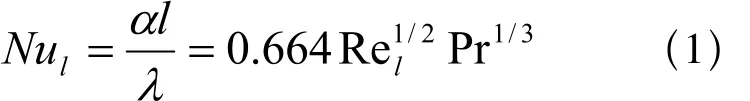
式中,Nul和Rel中的特征长度是平板的全长,上式在Rel≤2×105的范围内适用。
流体垂直平板时,平板表面平均换热系数计算公式如下:

其中特征长度为平板长度,定性温度为(t∞+tw) / 2,适用范围 Re=4×103~ 1.5×104。
1)对于外流平行平板的情况,即状态III,当压力由1atm变到0.3atm时,密度也会降为降为原来的0.3倍,因此,Nu 变为原来的0.55倍,即降低了45%,相应的平均换热系数也降低了45%;
2)对于气流垂直平板的情况,即状态I和II,当压力由1atm变到0.3atm时,Nu 变为原来的0.42倍,即降低了58%。但由于压力变为0.3atm时,式(2)已经不再满足适用范围,降低值误差较大。
2.2 流场和温度场结果
平板周围气流分布是决定平板通风换热特性的关键因素,计算中没有考虑气流温度对密度的影响,因此,在相同压力下状态I和II平板周围流场相同,只是由于发热面与来流方向相反导致换热量不同,温度场有所差异。当气流直接冲刷发热面时,平板换热效果要好一些,相应的温度低。由计算可以发现状态II和III平板温度最大值相近,均比状态I高,说明平板在状态I通风换热性能最好。
在计算中发现,在通道体积流量不变情况下,平板最高温度值随压力降低而增加,图4给出压力为1atm和0.3atm时状态II平板周围流场和温度场分布。平板周围流场分布并没有随压力变化而改变,只是参与换热气体质量降低,导致平板换热系数降低,温度升高。
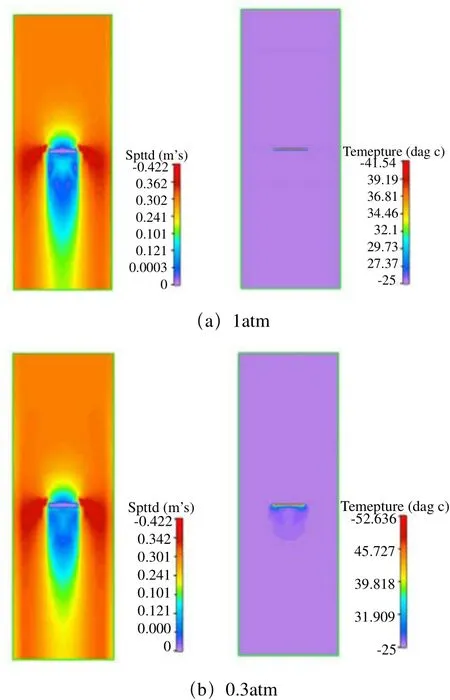
图4 不同压力下状态II速度流场和温度场分布
2.3 表面平均换热系数及平均温度分布
图5给出三种状态下平板发热面平均对流换热系数和平均温度随压力的变化曲线。由图可看出:1)随着来流方向与发热面关系的不同,铝板换热特性也有所差别,其中第一种状态最好,第三种次之,第二种最差;2)随着通道内压力降低,铝板换热特性变差,表面温度提高,平均对流换热系数降低;3)压力降低对三种状态铝板换热系数影响程度各不相同,对第二种状态影响最大,对第一种影响最小,这是因为流场形式不同,参与换热气体量降低对换热效果的影响程度也不同;4)当压力由1atm变为0.3atm时,三种状态对流换热系数降低幅度都低于理论值,出现这种现象的原因除了计算条件与经验公式应用环境差别之外,另外一个原因还在于经验公式计算和数值模拟中均假设温度变化对气流密度没有影响。
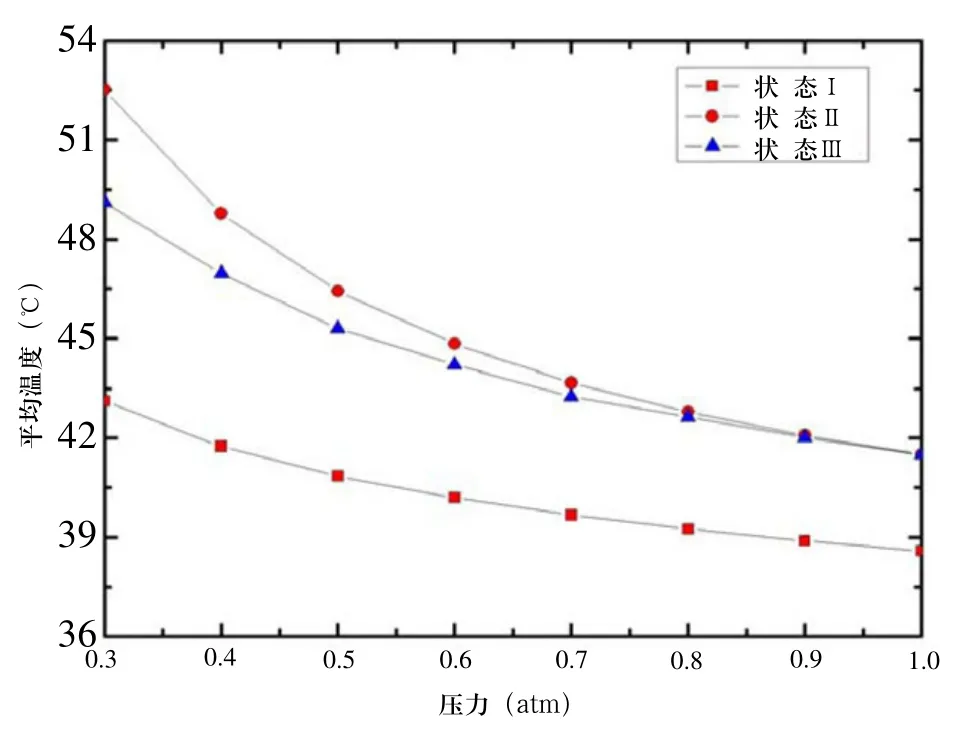
图5 三种工况下发热面平均温度随压力变化曲线

图6 三种工况下发热面平均对流换热系数随压力变化曲线
3 结论
经过对不同压力下气流冲击平板换热特性的研究发现,随着压力的降低,平板发热面换热系数降低,但降低的幅度会随着与来流方向不同而不同。在目前计算条件和0.3atm压力下,发热面换热系数降低的幅度在25%~48%之间,小于经验公式得出的结论,这给飞行器自主飞行过程中,舱内设备的通风系统设计提供一定的理论依据。
[1] 杨世铭, 陶文铨. 传热学[M]. 北京: 高等教育出版社,2006.
[2] 陶文铨. 数值传热学[M]. 西安交通大学出版社, 1988.

