汽车制动防抱死系统控制策略的仿真研究
张红英,蔡进军
(1. 黄冈职业技术学院 交通学院,黄冈 438002;2. 武汉理工大学 汽车工程学院,武汉 430070)
0 引言
ABS系统即制动防抱死系统,是为了防止车辆在紧急制动时车轮抱死和丧失转向能力的主动安全系统。相比普通制动系统,ABS有效改善了制动时的行车稳定性、操作性,充分发挥制动器效能,并减小轮胎磨损,制动安全性大为增加。
ABS系统的控制目标是选择合适的控制策略,根据所选的控制变量(滑移率或者轮速),使车辆在制动时的滑移率在最佳值附近。目前ABS系统主要采用逻辑门限值控制、滑模变结构控制、PID控制、模糊控制等控制策略。
1 ABS系统的控制策略
1.1 逻辑门限值控制
逻辑门限值控制是确定一个期望滑移率,当系统检测到的实时滑移率大于预先设定的参考值时制动系统降压,其余时间增压。通常根据经验确定增压与降压的幅度,该控制策略的优点是不涉及具体的控制数学模型,被广泛应用,缺点是互换性较差,需要做大量的实验才能获取到经验参数,其控制逻辑较复杂,控制不够平稳。
1.2 滑模变结构控制
滑模变结构控制是一种非线性的控制策略,其根据系统当时的状态、偏差以及导数值,用理想开关的方式切换控制量的大小及符号,使系统在切换线邻近区域来回运动。该控制策略依赖于车辆的数学模型,无法对多体动力学模型进行控制。
1.3 PID控制
PID控制策略是基于滑移率的控制,系统将实际滑移率控制在最佳滑移率点。这种系统从理论上讲是最好的,但它实施难度大,特别是不易确定最佳滑移率点,而且基本上依靠试凑法来取控制参数,缺乏理论依据,所以进行这方面的理论研究及模拟工作比较多,不能被广泛用于现有实际系统的控制。
1.4 模糊控制
模糊控制是一种基于经验规则的、并列型的开关控制,可较好地适应动态变化工况非线性时变系统(车辆控制过程)。利用模糊逻辑控制的ABS在制动过程中,利用制动时车辆的运动特征与路面特性间的关系估计路面状况,以确定不同路面的最佳滑移率,根据滑移率和滑移率误差的变化量确定ABS制动压力调节器的调节压力。
2 制动防抱死系统的控制策略研究和仿真
2.1 基于逻辑门限值控制方法的仿真模型建立
通常用单论模型对车辆的运动状态及受力情况进行分析,建立车辆的单轮模型可以大大简化复杂的动力学模拟过程,易于描述制动过程。车轮在制动时的受力情况如图1所示。
由上图可建立单轮模型的动力学方程:


图1 轮胎制动时的受力
方程式中的G是汽车质量,μ是附着系数,F是地面的支撑力,R是汽车轮胎半径,M是汽车制动时的制动力矩,F是地面附着力,v是汽车速度,ω是轮胎角速度,I是车轮等效转动惯量。
路面模型选择干沥青路面,附着系数与滑移率的关系为:
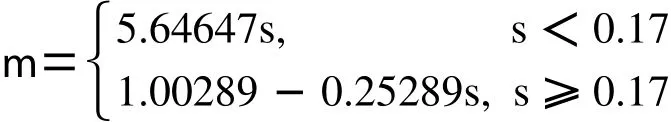
制动系统可简化成一个一阶惯性环节,在制动时系统进入压力稳定阶段后,可认为制动压力与力矩成线性关系,比例因子为Kf。
在Simulink中搭建的ABS仿真模型如图2所示。

图2 基于逻辑门限值控制策略的仿真模型
模型中先设置期望滑移率,并在预先设置的一维查表模块输入干沥青路面下滑移率和附着系数的关系,根据滑移率定义式和式(2)计算出相对滑移率,然后将计算值输入到比较模块,借助sign函数控制器,控制轮压的增减,以达到反馈控制轮角速度的目的。
2.2 基于模糊控制方法的仿真模型建立
模糊控制方法的核心部分是模糊控制器的设计。模糊控制器在工作过程中首先将输入量进行模糊化处理,然后进行模糊推理,再清晰化处理推理得出的模糊量,最终将清晰控制量输出。对ABS仿真中,把理想滑移率和实际滑移率之差作为模糊控制器输入量。模糊控制方法原理如图3所示。

图3 模糊控制方法原理图
Simulink中有专为模糊控制策略仿真所定制的模糊控制箱工具,利用该工具可方便的对ABS模糊控制器进行设计。ABS的模糊控制系统对输入量滑移率误差E和滑移率误差变化率Ec进行模糊化处理;输出量为制动压力变化量U。当设定的初始最佳滑移率为0.2时,则滑移率误差的变化范围为(-0.2,0.8),滑移率误差的变化率Ec的变化范围取为(-6,6),制动压力变化量U的取值范围为(-6,6)。分别设计输入量滑移率误差E、滑移率误差变化率Ec和制动压力变化量U的隶属度函数如图4所示,以使制动压力变化量U对应快速减压(NB),中速减压(NM),慢速减压(NS),保压(ZE),慢速增压(PM),中速增压(PM),快速增压(PB)7个状态。设置时要保证论域的不对称性。
设置完隶属度函数后,需要编辑模糊规则,通过”If E is()and Ec is()then U is()”语句建立滑移率误差及其微分输入量和压力变化输出量的逻辑关系,以满足ABS工作中压力变化的7个状态,建立好的49条规则如表1所示,并在模糊逻辑编辑器中输入表中的逻辑关系。
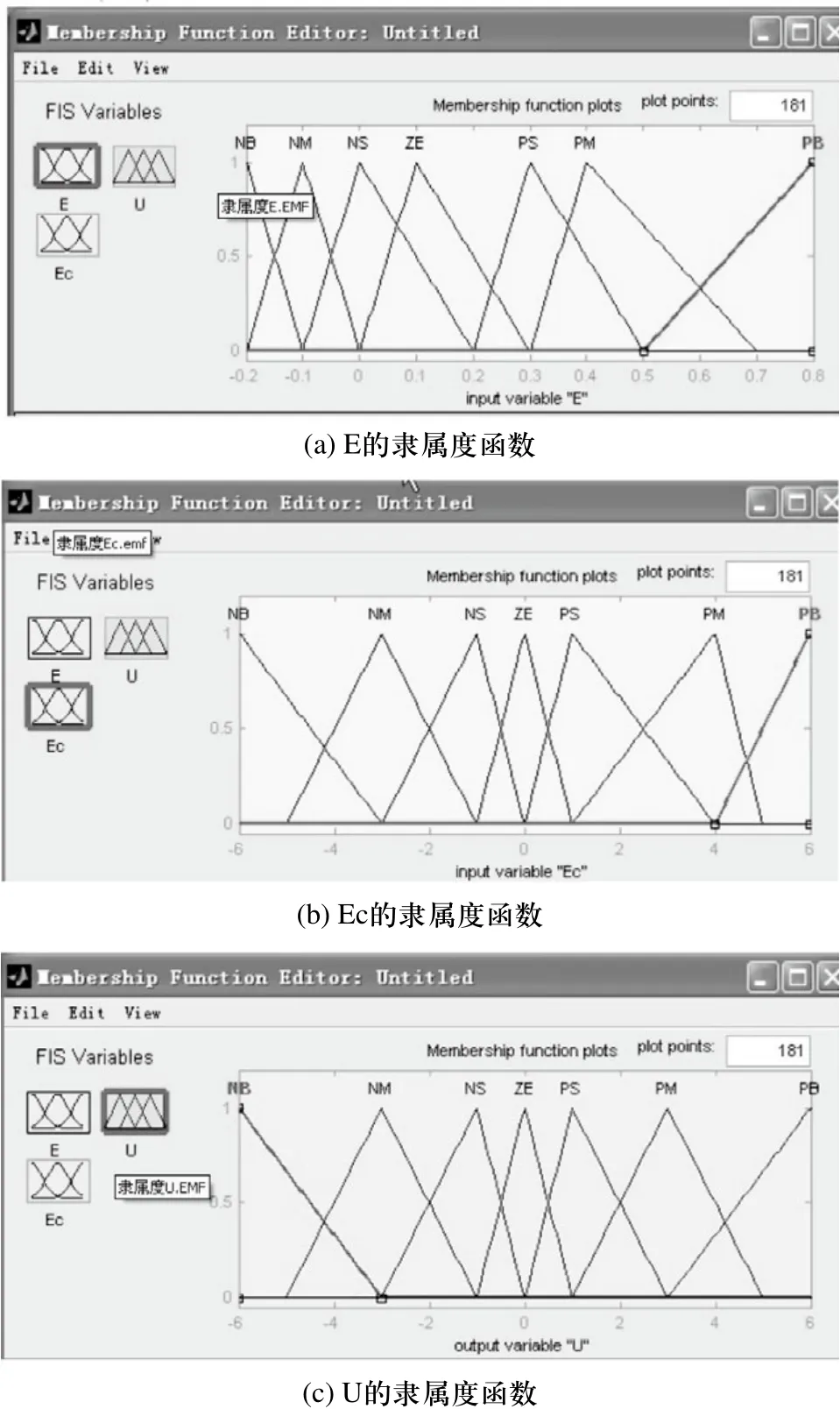
图4 设置变量的隶属度函数
输出控制规则三维曲面如图5所示。

图5 控制规则三维曲面
搭建的基于模糊控制策略的仿真模型如图6所示。
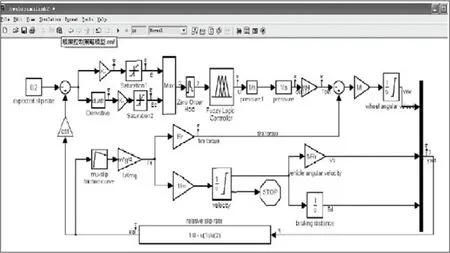
图6 基于模糊控制控制策略的仿真模型
模型中,E和Ec的比例因子分别设置为1和0.4,以达到最快的仿真效果。和逻辑门仿真模型不同的是,因为模糊控制器输出的是轮缸压力变化速率的变化值,需经过两次积分获得轮缸压力。模型中还采用零阶保持器以加快仿真速率。
2.3 仿真结果分析
2.3.1 基于不同控制策略的ABS制动效果比较
由图7中可以看出,无ABS的车辆,制动后不久就达到抱死状态。而有ABS的车辆,无论用哪种控制策略,都没有在车辆停止前抱死拖滑,验证了ABS具有预防车轮抱死的效果。基于逻辑门限值控制策略的车辆滑移率在理想值0.2附近反复波动;而模糊控制策略仿真的滑移率曲线平缓接近0.2,这是因为模糊控制器中拟定的制动压力变化规律受到滑移率误差和其变化率的影响,不会出现很大的波动,仿真曲线和控制规律相一致。
由图8所示,比较其制动距离曲线可以看出,有ABS的车辆制动距离较短,这是因为制动曲线在理想值附近,充分利用了路面附着力的缘故,所以装载ABS的车辆制动性能也较好。上图中还可以发现,采用逻辑门控制的ABS制动距离要比模糊控制的ABS制动距离更短,效果更好。
2.3.2 基于不同附着系数路面的ABS制动效果比较
将干沥青路面模型换为疏松积雪路面。附着系数和滑移率的关系为:

在逻辑门控制下的ABS制动效果曲线比较如图9和图10所示。
由仿真结果可知,因为疏松积雪路面的附着力比干沥青路面低,因此更容易打滑,滑移率曲线的波动较大,制动距离较长,所以即使安装了ABS的车辆,在冰面、雪地等低附着路面行驶时,驾驶员需要注意行车安全,低速行驶。

图7 两种控制策略下的滑移率比较

图8 两种控制策略下的制动距离比较
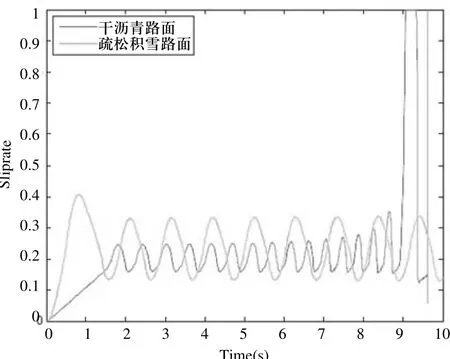
图9 干沥青路面和疏松积雪路面滑移率比较
3 结论
ABS是提高汽车主动安全性能的重要装置,虽然ABS有极其成熟的市场,但份额基本被国外公司垄断,国内对于ABS的研究还处在起步阶段,在ABS的结构和控制策略的设计上还需不断的深入。本文主要介绍了目前应用于ABS的不同的控制策略,分析了ABS制动过程中的动力学模型,使用Matlab中的Simulink模块分别对基于逻辑门限值控制策略和模糊控制策略的ABS进行了建模仿真,从滑移率和制动距离入手讨论了不同控制策略对车辆制动性能的影响,以及不同路面下ABS性能的差异。从而得到了ABS系统的工作规律,为深入开展汽车ABS的研究提供了有价值的参考和指导意义。

图10 干沥青路面和疏松积雪路面制动距离比较
[1] 麻友良. 汽车电器与电子控制系统(第2版)[M]. 北京: 机械工业出版社, 2011.
[2] 高玉民, 王正润. ABS防抱制动系统[M]. 福建: 福建科学技术出版社, 2001.
[3] 魏朗, 王囤编. 现代汽车制动防抱死系统实用技术[M].北京: 人民交通出版社, 2001.
[4] 黎军主. 汽车制动电子控制系统检测与维修[M]. 北京:人民交通出版社, 2004.
[5] 李开春. 基于车轮滑移率的ABS控制算法研究[D]. 江苏大学, 2006.
[6] James D. Halderman, Chaes D. Mitchell, Jr. Automotive brake systems [M]. New Jersey: Pearson Prentice Hal, 2004.
[7] 余志生. 汽车理论[M]. 北京: 机械工业出版社, 2009.
[8] 蔺玉辉. ABS模拟仿真与模糊控制设计[D]. 东北大学,2005.
[9] 于东. 制动防抱死系统(ABS)控制方法仿真研究与控制器设计[D]. 山东大学, 2007.
[10] 侯光钮. 车辆防抱死制动系统的控制技术研究[D]. 东南大学, 2005.
[11] Sun Jun. Development of Fuzzy logic Anti-Lock Braking System for Light Bus. SAE paper No. 2003-01-0458.
[12] A Simulation of Vehicle Lateral Stability Based on Fuzzy PID Control[C]. 2009 International Conference on Measuring Technology and Mechatronics Automation. 2009: 194-199.
[13] 苟凯英, 等. 基于MATLAB仿真环境实现防抱制动控制逻辑[J]. 测控技术, 2002, 21(1): 25-27.

