基于最小二乘曲线拟合法的皮带垂度与张力关系研究
梅 松,周月娥,李东波,童一飞,袁延强
(1.南京理工大学 机械工程学院,南京 210094;2.钟山职业技术学院 机电与汽车工程系,南京 210049;3.南京三埃工控股份有限公司,南京 211106)
0 引言
影响皮带秤称重系统精度要素之一就是张力,利用张力补偿可以提高称重长期稳定性和精度。张力越准确,称重就越精确。因此,准确测得张力值十分重要。另外,张力不稳定是由机械的不平衡与磨损和电机响应运转等方面造成的[1]。本文通过检测皮带垂度并对垂度数据进行算法处理,从而对张力的不稳定因素进行补偿,最终根据研究得到的垂度与张力数学模型来计算出张力。
本文先理论推导出张力随流量变化的数学模型,其次,通过离散垂度测量来建立垂度与流量的数据表,利用最小二乘曲线拟合法对垂度与流量曲线拟合,实现对数据的综合分析,为研究物料流量与皮带垂度的关系提供科学的参考依据[2]。然后对拟合结果进行分析,最终得到垂度、皮带倾角等参数的张力数学模型。
1 现场输送带载料模型分析
现场的输送带安装示意图如图1所示,在具体研究中简化为图2所示模型。
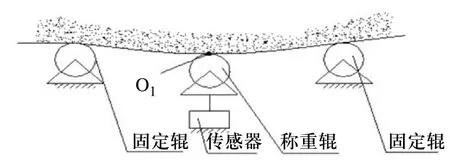
图1 现场输送带载料
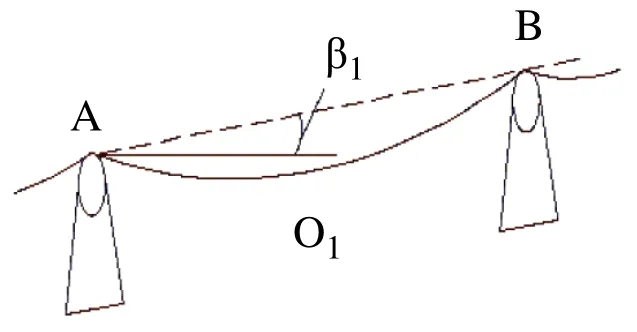
图2 现场输送带载料简化模型
其中,O1为托辊A,B之间输送带上的垂点,AB倾角为β1,其中虚线是输送带传输方向,实心直线为水平面,=L,根据实际测试,O1垂点对应的输送带挠度即垂度v<3%L。现取一小段输送带O1D分析,建立xo1y坐标系,如图3所示。
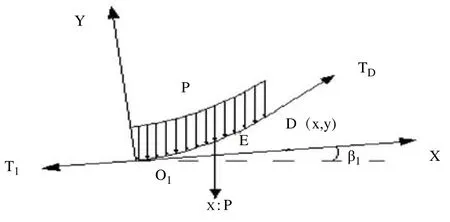
图3 输送带O1D段受力分析图
取O1为坐标原点,且以过O1点的切线为X轴,与X轴垂直作Y轴,其中,T1,TD分别为O1和D点处的张力,P为均布载荷;D点坐标为(x,y),载荷重心坐标E(xe,ye),因输送带挠度较小,曲线O1D近似等于x。因此,O1D上负荷可视为平衡条件可得:
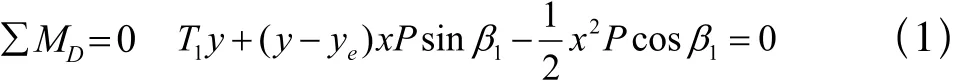
式中,MD为关于D点的力矩,P为皮带及物料的质量分布简称流量, β1地面与水平面间的夹角。经整理得:
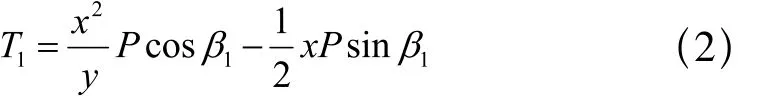
又已知O1为AB垂点,且为中间,因此可得x=L/2,代入上式得:
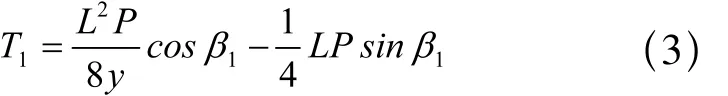
式中,L为两托辊间的距离。其中,L与β1均为已知量。当P与y两个变量检测出来,对应O1点的张力也就随之求出。
2 基于最小二乘法的垂度-流量曲线拟合
2.1 最小二乘法曲线拟合原理
假设流量fi与垂度xi,其中i=0,1,2,…,n。拟合关系为n次多项式,函数为其中a0,a1,…,an为下面方程组的解:
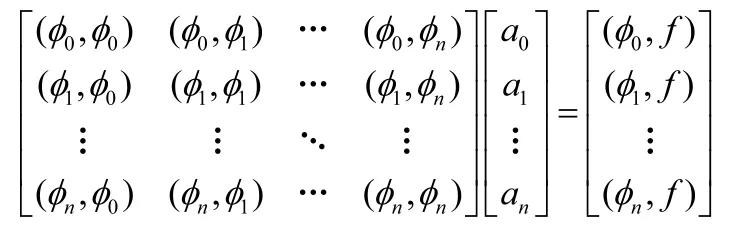
如果方程组中的系数矩阵为非奇异,则最优解唯一,这里 , 是Rm+1上向量的加权内通过该方程使用Matlab软件求解出系数a0,a1,…,an,就可以解得n次多项式[3]。
由于皮带传输物料的重量不均匀,只有通过垂度值来反推出流量,从而进一步估算载物的重量,辅助称重系统判定称重单元计算结果的正确性与故障源。因此,研究物料流量固定,通过大量数据采样得到垂度值,经均值数据处理,得到一组垂度与流量的数据,重复该方法获取多组不同流量下检测到的垂度值,来准确反映流量与垂度的关系。
2.2 流量与垂度实验
实验条件:1)标定初始值104mm;2)输送带预紧力为840kg;3)皮带宽为1.2m;4)料斗下料给定值设为100t/h。
本实验通过改变电机驱动输送带运转的频率来改变落在输送带的物料重量即流量,并检测获取相应的垂度,得到表1所示的9组流量范围在14.62~46.3kg/m内的垂度与流量的关系数据。
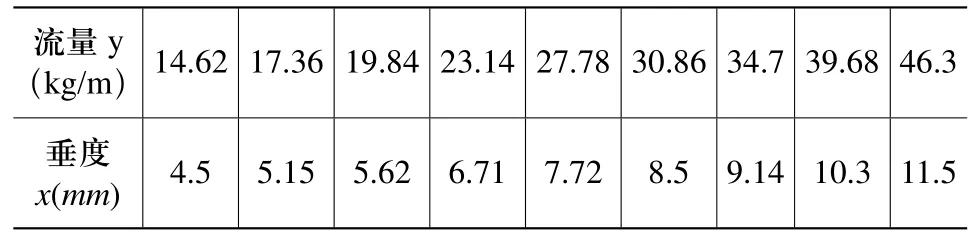
表1 垂度与流量数据关系
2.3 垂度-流量特性研究
根据表1数据采用Matlab对拟合模型y=a0x0+a1x+…+anxn进行多项式拟合,由最小二乘法确定多项式的系数a0,a1,…,an,通过拟合发现高于5次多项式曲线就会严重失真,因此只考虑5次以内拟合曲线,通过Matlab计算获得各多项式曲线对应的残差如表2所示。

表2 多项式拟合曲线残差
由表2可以观察到5次多项式拟合曲线残差为0.80778,拟合效果最好,其拟合曲线如图4所示。
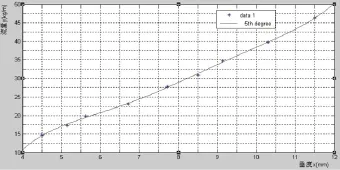
图4 5次多项式拟合曲线
由图可以观察出数据与曲线拟合度非常好,因此选取5次多项式拟合曲线为最优拟合曲线,线方程[4]如下:
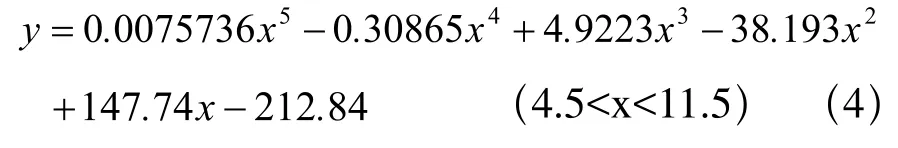
另外,根据皮带本身性能和受力情况分析可以设想曲线y=f (x)是双曲数据规律大致符合,可以通过变量代化为线性参数的数学模型其中(i=1,2,…,9)。其中ti,zi分别由原始数据xi, yi据变量代换公式计算出来,转换后的数据表如表3所示。

表3 t,z关系数据
将以上计算值代入简化方程组得如下方程组:
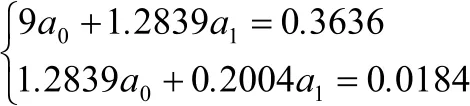
计算得a1=0.33822,a0=-0.0078494从而拟合曲线为
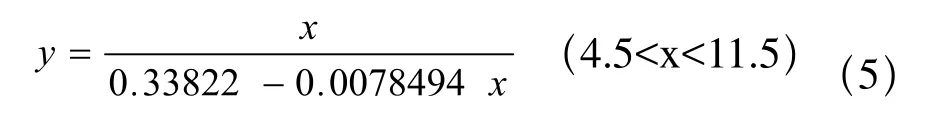
3 最小二乘法曲线拟合结果分析
3.1 拟合模型误差比较
根据实测垂度数据,分别利用5次和双曲型拟合曲线计算出输送带上的物料流量,进而计算出理论流量与计算流量之间的绝对误差,误差平方[5]。具体计算结果如表4所示。
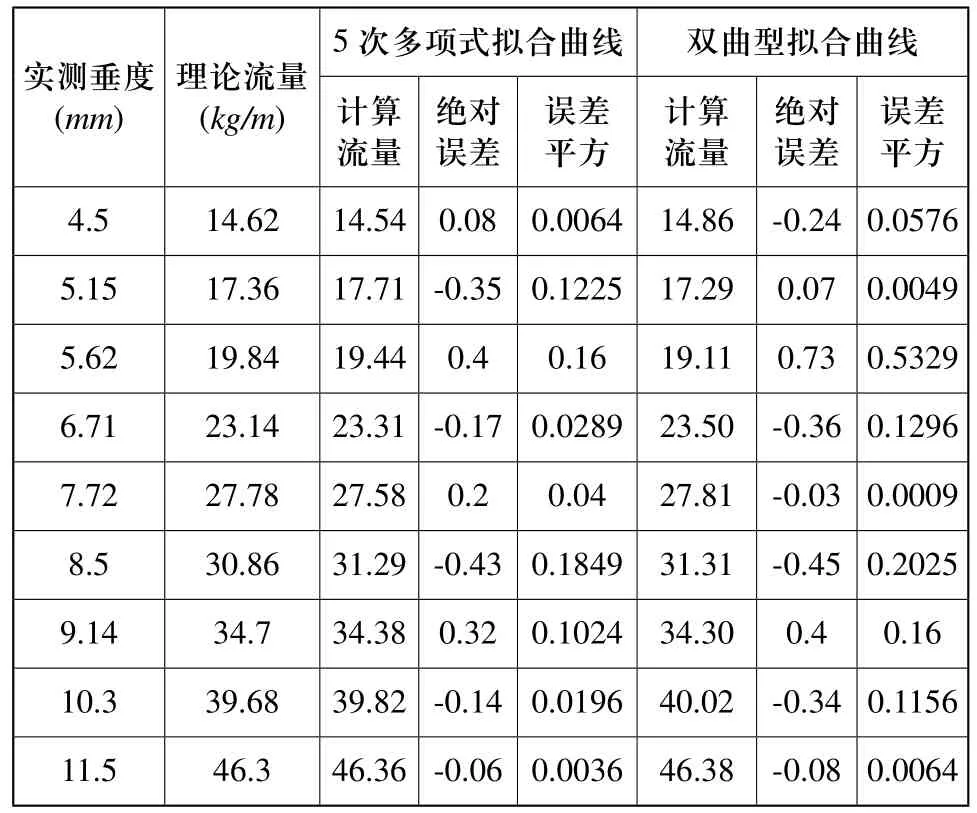
表4 5次多项式与双曲型拟合曲线参与拟合数据分析
由表4算得5次与双曲型拟合曲线误差平方总和分别为0.6683,1.2104。5次多项式拟合曲线误差平方更小,拟合效果更好。
由上表分析研究选择5次多项式拟合曲线作为最优曲线拟合结果,其函数如下:
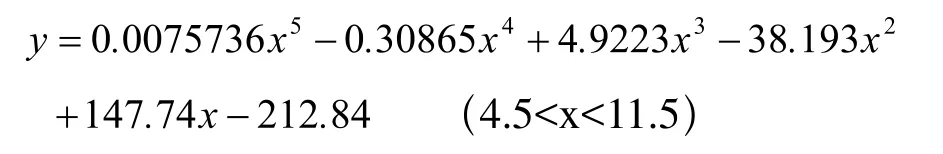
3.2 张力数学模型
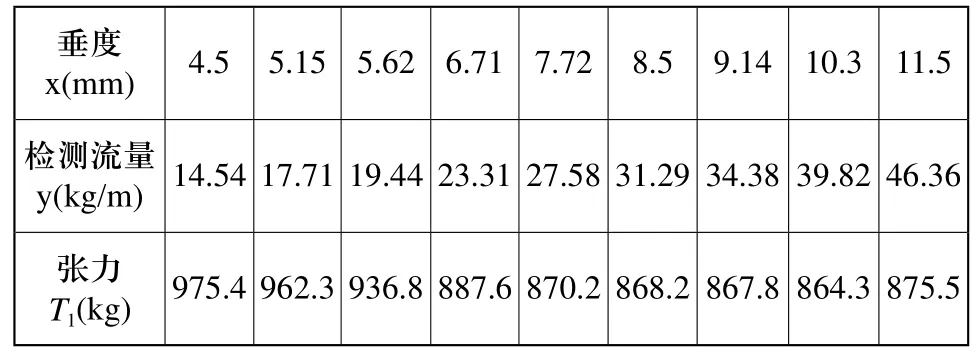
表5 垂度、流量与张力关系
从表5中可以观察到垂度为4.5~10.3mm范围内张力随着垂度变大而减小,张力的极小值产生于垂度为10.3mm~11.5mm之间,张力自极小值之后会随着垂度的增加而增加,由以上规律可判定张力与皮带性能有很紧密的关系,可以在以后的实验中作进一步研究。最终形成的张力与垂度的数学模型为:
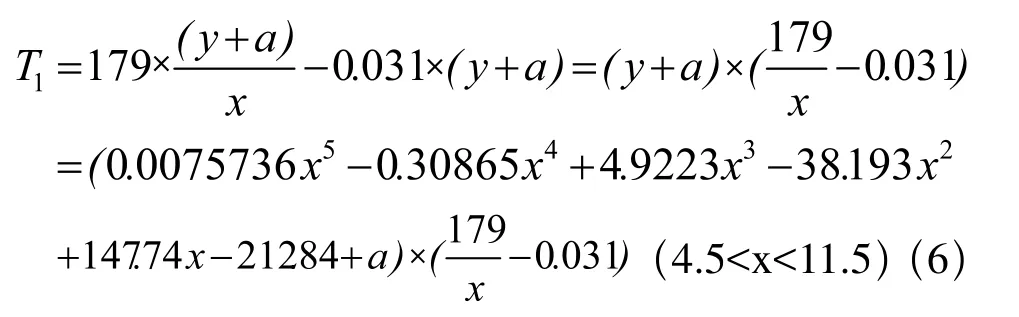
若将参数β1,L代入公式则可以转化为
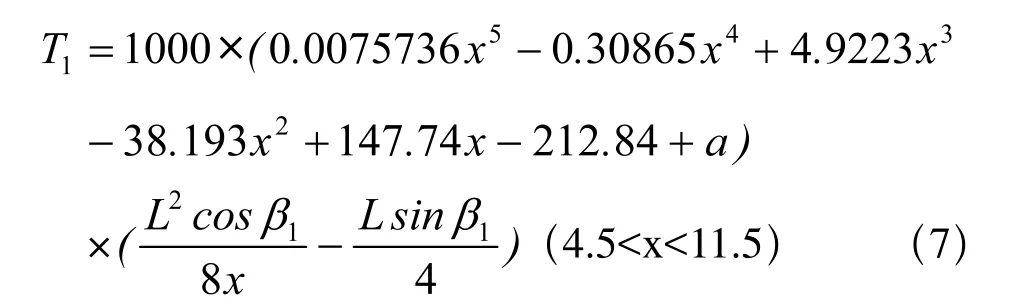
式中a为皮带重量分布(kg/m);x为测得的垂度值(mm); T1为张力(kg);β1为皮带与水平地面之间的夹角;L为两托辊之间的距离(m)。
由公式(7)可以根据检测到的垂度推算出张力。
4 结论
1)通过实验获取了流量与垂度关系的对应数据;利用最小二乘曲线拟合法研究垂度与流量的实验数据,得到垂度与流量关系的拟合曲线;通过实验验证分析得出5次多项式拟合曲线为最优垂度与流量拟合曲线。2)根据最优垂度与流量拟合曲线及张力与流量数学关系建立了皮带张力与垂度的数学模型。
[1] 李南, 刘秋楠. 有关高速传带设备张力控制的应用研究[J]. 制造业自动化, 2010. 2, 32(2): 132-133.
[2] 谢先伟. 最小二乘法在煤矿钻机测试中的应用研究[J].制造业自动化, 2011. 5, 33(9): 59-60.
[3] 徐跃良. 数值分析. 成都: 西南交通大学出版社, 2005,08: 59-60.
[4] 吕喜明, 李明远. 最小二乘曲线拟合的MATLAB实现[J].内蒙古民族大学学报(自然科学版), 2009. 3, 24(2): 126-127.
[5] 刘晓艳, 芮雪, 刘小勇. 基于正交多项式作最小二乘曲线拟合的水位流量率定系统设计与实现[J]. 新疆农业大学学报, 2009, 32(3): 89-90.
——垂度法

