谐波传动柔轮应力与位移二维简化分析
李若亭,马德军,王家梁,李晓飞,孙亮亮
(装甲兵工程学院 机械工程系,北京 100072)
0 引言
谐波齿轮传动是二十世纪50年代末和60年代初问世的一种崭新传动[1]。它与一般齿轮传动相比,具有传动比大、体积小、重量轻、精度高及噪声小等优点。近几十年来,谐波齿轮传动技术被广泛应用于仪器仪表、汽车、机器人、精密光学设备等各个领域[2]。普通谐波传动的柔轮在变应力工况下易产生疲劳破坏,主要表现为疲劳断裂,因而柔轮强度的研究是谐波齿轮传动研究的重要方向,其中以柔轮变形与应力研究为重点[3]。随着科学及计算机技术的发展,有限元法在谐波齿轮设计和应力分析中已显示出巨大的优越性,可以精确计算分析出柔轮齿根应力应变数值。本文应用ABAQUS软件建立了谐波传动平面简化模型,通过对谐波传动中凸轮式波发生器结构进行不同方式的等效处理,建立有柔性轴承以及无柔性轴承的模型分别进行了有限元数值计算,分析比较了两种模型柔轮的应力及径向变形规律,对谐波传动分析研究有一定的指导意义。
1 建模及有限元分析
现以双波谐波齿轮为研究对象进行分析,其减速比i=100,模数m=0.6mm,压力角α=20°;柔轮齿数ZR=200,变位系数xR=3.86,齿顶高系数=0.5,顶隙系数=0.5;刚轮齿数ZG=202,变位系数xG=3.992,齿顶高系数=0.5,顶隙系数=0.5。刚轮材料为45钢,其弹性模量E=206Gpa,泊松比μ=0.3,柔轮材料为30CrMnSiA,弹性模量E=210Gpa,泊松比 μ=0.3。
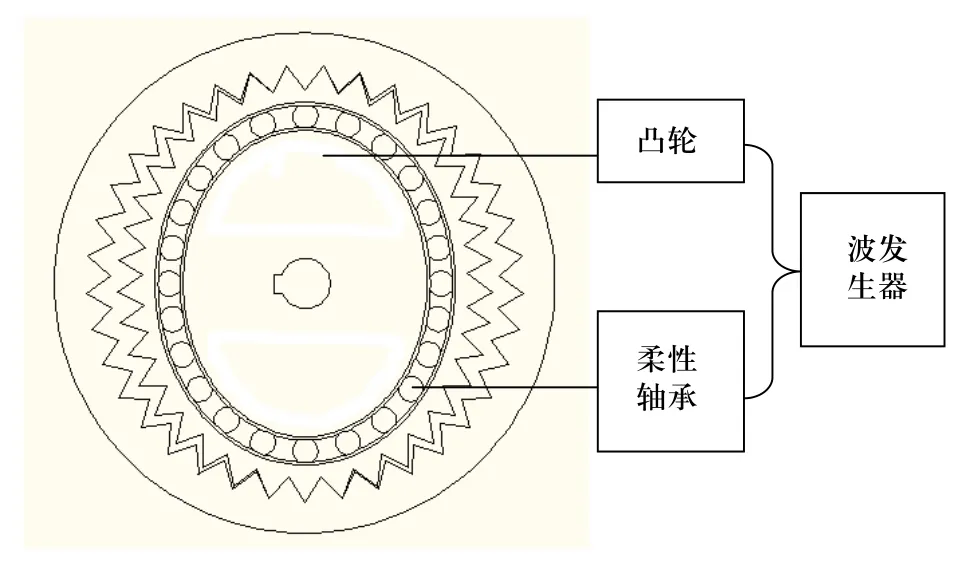
图1 凸轮式波发生器谐波传动示意图
凸轮式波发生器通常由凸轮及柔性轴承组成,如图1所示。其特点是径向刚度好、形成的特征曲线稳定性好、组件装配简单和易标准化。但是带有柔性轴承的凸轮式波发生器接触对多、建模复杂,应用现有的有限元数值方法难以直接分析计算。因此,建模过程中必须对波发生器的柔性轴承结构进行简化或者省略处理[4]。以下在ABAQUS中分别建立有柔性轴承以及无柔性轴承两组模型,为了提高计算效率,可用二维模型近似代替三维模型。
1.1 有柔性轴承的谐波传动模型
实际建模中,考虑到柔性轴承滚动体与轴承内外圈之间接触复杂,为简化模型,可对波发生器柔性轴承结构作等效处理,将滚动体与轴承外圈固联,并简化输入轴键槽结构,如图2所示。
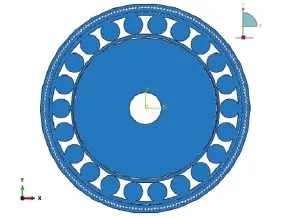
图2 未装配情况下有柔性轴承的谐波传动模型
由文献[5]设计分析得,柔性轴承外圈壁厚δWj=2.4mm,内圈壁厚δNj=1.8mm,滚动体直径dg=12mm,滚动体个数N=22,凸轮长半轴直径L1=90.1224mm,短半轴直径L2=87.4776mm。凸轮材料为40CrNiMoA,弹性模量E=210Gpa,泊松比μ=0.3,轴承材料GCr15,弹性模量E=208Gpa,泊松比μ=0.3。凸轮与轴承内圈、轴承外圈与柔轮之间接触区域摩擦系数ftn=fwr=0.1,滚动体与轴承内圈接触等效为滚动摩擦系数fwn=0.002,柔轮与刚轮齿面摩擦系数frg=0.05。
1.2 无柔性轴承的谐波传动模型
在谐波传动过程中,考虑到凸轮迫使柔轮发生变形,柔性轴承仅起到变滑动摩擦为滚动摩擦作用。为了提高计算效率,可以将波发生器结构进一步简化,以柔性轴承的外廓线作为凸轮的轮廓线,如图3所示。
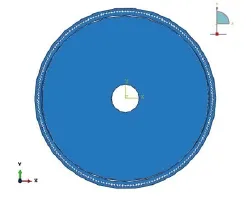
图3 未装配情况下无柔性轴承的谐波传动模型
1.3 分析步设置及网格划分
谐波齿轮传动仿真可以分为装配过程和波发生器旋转带动柔轮的传动过程。本文采用通用模块(Standard),使用隐式算法定义两步分析步:1)为谐波齿轮传动组建的装配,定义凸轮及刚轮在平面内的三个自由度U1=U2=UR3=0;2)为凸轮转动,定义刚轮U1=U2=U3=0,凸轮U1=U2=0、UR3=6.28(rad)[6]。
采用四节点平面应力单元CPS4R对轮齿进行智能网格划分,并在装配及传动过程中参与啮合计算的轮齿齿侧及齿根处适当加密。装配后模型啮合区域网格划分如图4所示。
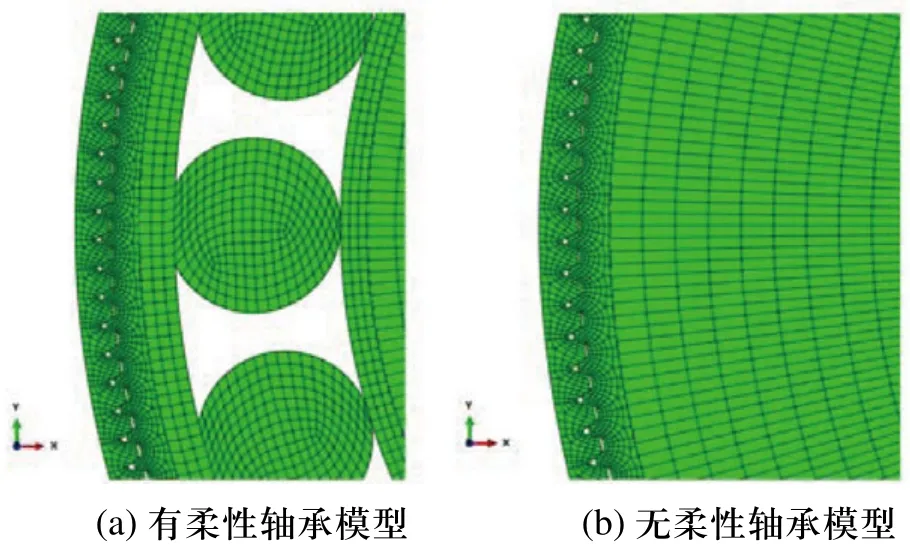
图4 装配后谐波传动模型啮合区有限元网格
2 计算结果比较分析
ABAQUS中的Visualization模块通过彩色云图显示分析部件的应力及位移分布,能形象逼真的表现谐波齿轮传动各部件的应力及位移分布情况。
2.1 柔轮应力结果比较分析
由ABAQUS有限元分析,计算出了各个节点变形后的Mises应力,两组模型装配后柔轮长轴方向Mises应力云图,如图5所示。

图5 装配后柔轮长轴方向Mises应力云图
由图5可以看出,有柔性轴承和无柔性轴承谐波传动模型装配后柔轮的应力分布一致,应力最大区域均位于柔轮长轴方向对应齿根位置,与此同时,齿顶及齿面方向应力值较小。由于有柔性轴承模型在长轴方向为单个滚动体接触,受力不均匀,所以齿根最大应力值稍大,为123Mpa;无柔性轴承模型凸轮与柔轮接触,受力均匀,齿根最大应力值稍小,为113Mpa。总体而言,两组模型柔轮齿根应力相差不大,数值近似相等。
2.2 柔轮径向位移结果比较分析
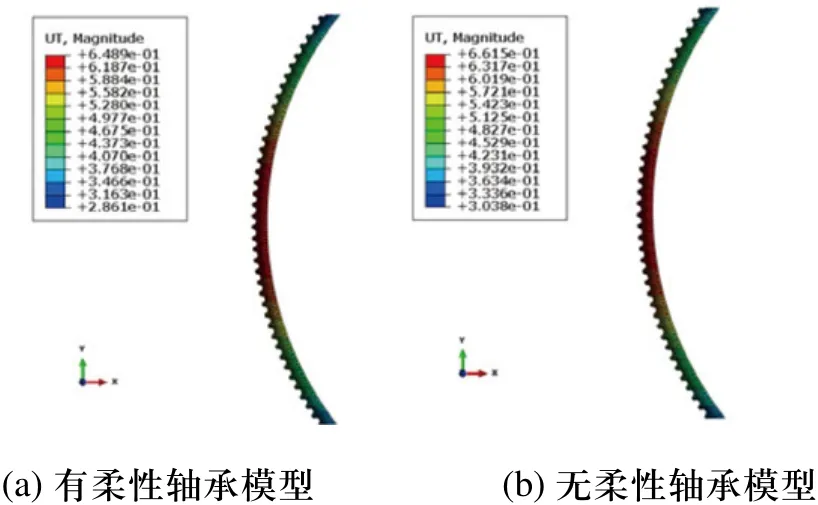
图6 装配后柔轮长轴方向径向位移云图
图6所示为谐波传动模型装配后柔轮长轴方向径向位移云图。由图中可以看出,有柔性轴承和无柔性轴承谐波传动模型的柔轮径向位移云图分布一致,位移最大区域均位于柔轮长轴方向,长轴附近轮齿不参与啮合区域径向位移则相对较小。由于柔性轴承径向刚度较小,装配后易产生径向弹性变形,所以具有柔性轴承的模型其柔轮在装配后相对于初始位置位移较小,最大径向位移为0.64mm。与此同时,无柔性轴承模型的波发生器径向刚度较大,几乎没有径向弹性变形,因而柔轮位移量稍大,最大径向位移为0.66mm。总体而言,两组模型柔轮径向位移计算结果相差不大,数值近似相等。
3 结论
利用有限元分析软件ABAQUS,分别对凸轮式波发生器采取不同的简化方式,建立了有柔性轴承以及无柔性轴承的谐波齿轮传动模型,对装配后柔轮应力及径向位移进行了分析。结果表明,
无柔性轴承的谐波传动模型相对于有柔性轴承模型的柔轮应力及径向位移分布相同,数值近似相等。考虑到建模方便且计算成本较小,在使用有限元数值方法分析柔轮强度时完全可以采用无柔性轴承的模型代替有柔性轴承的模型。上述结果对谐波齿轮传动有限元建模分析有一定的指导作用。
[1] C.M.Musser. The harmonic drive breakthrough in mechanical drive design[J]. Machine Design, 1960, 4(16):35-38.
[2] 沈允文, 叶庆泰. 谐波齿轮传动的理论与设计[M]. 北京:机械工业出版社, 1985.
[3] 伊万诺夫M H. 谐波齿轮传动[M]. 北京: 国防工业出版社, 1987.
[4] F-E Rhéaume, H Champliaud, Z Liu. Understanding and modelling the torsional stiffness of harmonic drives through finite-element method[J]. Journal of Mechanical Engineering Science, 2009, 223(2): 515-524.
[5] 范又功, 曹炳和. 谐波齿轮传动技术手册[M]. 北京: 国防工业出版社, 1995.
[6] 庄茁, 张帆. ABAQU非线性有限元分析与实例[M]. 北京: 科学出版社, 2005.

