基于混合Beta分布的水中兵器可靠性鉴定试验方案研究＊

孟凡亮 周徐昌 刘 洪 谢 勇

（海军工程大学兵器工程系 武汉430033）

1 引言

水中兵器包括鱼雷、水雷、深水炸弹以及诱饵等装备，是集机、电、控、化等多学科与一体的复杂系统。现代武器装备技术复杂、造价昂贵，在研制定型过程中由于经费及时间限制，不可能加工大量的正样用于可靠性试验。在可靠性评定中应用Bayes方法，可以充分利用验前信息，在保证质量的前提下，可有效的减少试验量。产品的研制是一个以已有的型号为基础不断改进的过程，Bayes方法正是利用这种继承性来弥补现场试验信息的不足的。但是新型号的的改进部分却带来了新的不确定性，当先验信息量大而现场试验信息数据少的情况下评估的结果会过度趋向于验前信息，而现场试验信息被“淹没”而不起作用［1］而造成评价结果的偏差。在后来的研究中分别有学者提出了数据质量因子和继承因子的方法对Bayes方法进行改进，但对于可靠性试验的风险分析还不充分。本文采用引入了继承因子混合先验分布的方法，合理地考虑了验前信息的作用，得出在不同继承因子下的鉴定方案，并且推导出了双方风险的计算方法。

2 先验分布的确定

工作可靠度鉴定试验存在两种结果：成功和失败，系统可靠性可用二项分布函数描述。对于成败型产品的二项分布可靠性而言，记R为产品的可靠性，成败型试验（n，f）的似然函数为

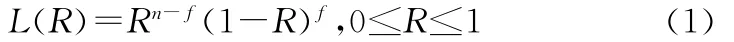
工程上一般考虑选取共轭验前分布β（R；a，b）作为可靠度R先验分布，即

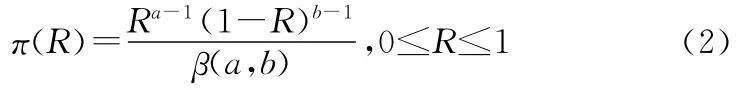
其中a和b为验前分布超参数，a和b的选取对于Bayes分析至关重要，许多学者讨论了验前分布中超参数的确定问题。本文采用矩估计法来确定超参数a和b。

设验前信息的一阶样本矩和二阶样本矩分别为μ1和μ2，可靠度R的一、二阶矩分别为

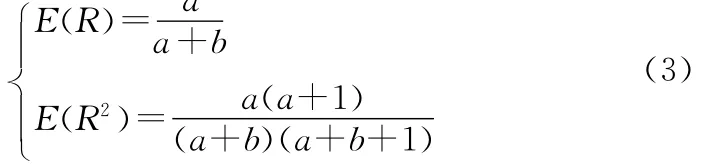
分别用一、二阶样本矩去估计可靠度R的一、二阶矩，得到a、b估计值

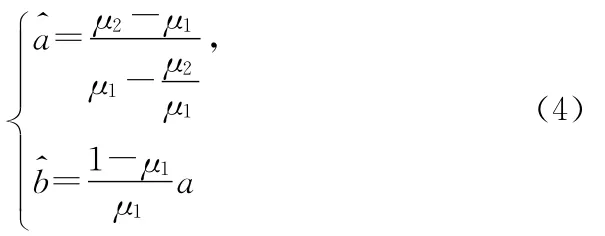
确定了验前分布超参数a和b后，若产品进行了n次试验，失效了f次，根据Bayes定理有

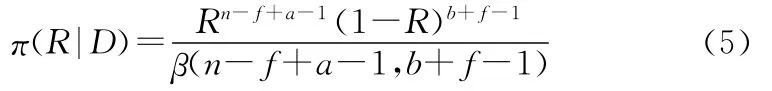
其中，D＝（n，f）表示试验信息，即R的验后分布为Beta（nf＋a，b＋f）。

Beta分布对二项分布模型进行可靠性评估，默认为对旧产品可靠性先验信息进行全面的继承，而任何新产品都有其独特的方面，这样产品就会产生不确定性。可以考虑用均匀分布来描述新产品不确定的方面，具有比较明确的物理意义。混合Beta分布为

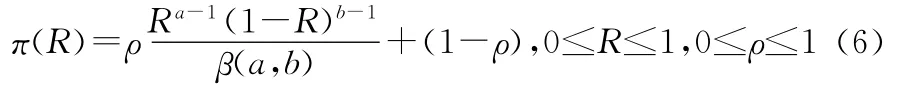
其中ρ称为继承因子，反映新产品与老产品的相似程度；（1－ρ）为更新因子，反映了新产品在改进时的不确定性。当ρ＝1时，两总体为同一总体，此时的混合先验分布就是一般意义上的共轭Beta分布；当ρ＝0时，两总体完全不一样，无任何先验信息，退化为无验前信息的Bayes估计。继承因子的引入，避免了对眼前信息的过度依赖，使可靠性评价结果更稳健。

继承因子ρ的选取非常重要，会对可靠性的验证和评估产生较大的影响，因此确定ρ就必须十分慎重。继承因子ρ表示新老向本的相似程度，如果新型号只是在老型号上进行较小的改动，ρ取较大的值；反之ρ取值相对较小。继承因子是相对变化情况的量化，可以利用卡方拟合优度的方法由验前信息和现场试验信息直接算出［2］，也可以由专家综合各方面信息后给出。

3 基于混合Beta分布的Bayes鉴定方案

取混合Beta作为二项产品成功率的先验分布，由式（1）和式（6）根据Bayes定理可以得出可靠度R的验后分布为

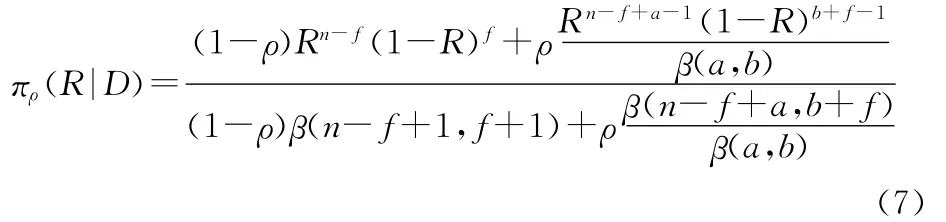
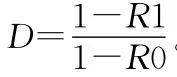
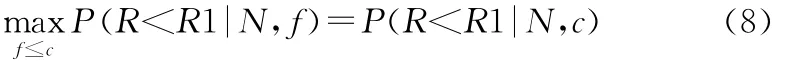
即按鉴定试验方案（N，c）接受产品时，产品可靠度R小于最低可接受值R1的最大后验概率。若给定使用方风险为β，则有

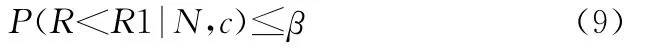
生产方承受的最大验后风险为

即产品被拒收时，产品可靠度R不低于可靠度目标值R0的最大后验概率。若给定生产方风险α，则有

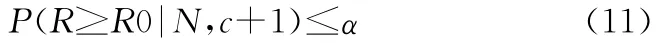
文献［1］中已经证明

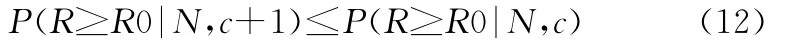
因此，混合Beta分布的Bayes鉴定方案需满足以下方程组

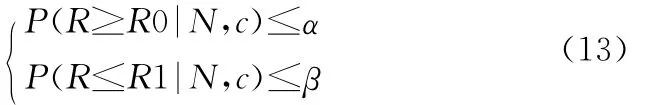
等价于

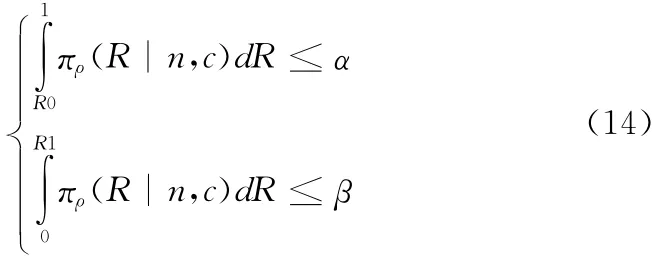
在给定可靠度目标值R0，可靠度最低可接受值R1，生产方风险α和使用方风险β后，解方程组（14）即可得到鉴定试验方案。求解过程中取方程组为等式，由于c取为整数，因此所得的鉴定试验方案（N，c）只能是方程组近似成立。

4 仿真算例

设合同规定的鱼雷可靠度目标值为R0＝0.85，鉴别比D＝2.0，生产方和使用方风险均为0.2。由经典方法得出的鉴定方案为（21，4），即试验条次数为21条次，失败次数不超过4次时通过试验。通过计算可得双方的实际风险为α＝0.1975，β＝0.1984。

假设试验以前的可靠度历史数据为0.694、0.803、0.793、0.910、0.842、0.919、0.870、0.885、0.718、0.848。通过方程组（4）可以算得，a＝21.594，b＝4.4242。为了方案比较的方便，取c＝4，当ρ取不同的值时可以得出不同的试验方案。

由表1可以看出，当ρ＝1时，验前信息被完全利用，可以大量节省试验样本，但当新产品与老产品与有差异时会比较激进；当ρ＝0时为采用无信息验前的Bayes估计方案，此时已经接近经典方案。根据专家信息恰当的选择ρ既可以发挥Bayes方法的优越性，而且可以使评定结果更加稳健。

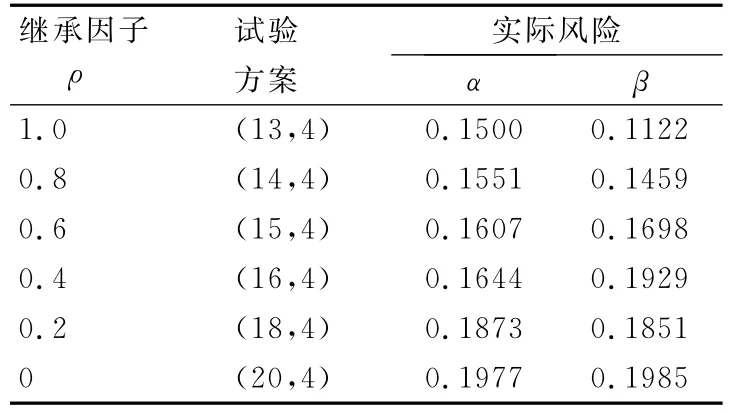
表1 不同继承因子时的试验方案比较

［1］毛昭勇，宋保维，胡海豹，等.基于先验信息可信度的鱼雷可靠性Bayes分析［J］.计算机仿真，2009，26（3）：37－39.

［2］姜礼平，张志华.成败型产品成功率鉴定的一种Bayes方法［J］.工程数学学报，2000，17（4）：25－29.

［3］张士峰.成败型产品可靠性的Bayes评估［J］.兵工学报，2001，22（2）：238－240.

［4］张士峰，樊树江，王慧频.复杂系统的Bayes可靠性评估［J］.航天控制，2002（2）：72－79.

［5］李鹏波，谢红卫，张金槐.考虑眼前信息可信度时的Bayes估计［J］.国防科技大学学报，2003，25（4）：107－110.

［6］王玮，周海云，尹国举.使用混合Beta分布的Bayes方法［J］.系统工程理论与实践，2005（9）：142－144.

［7］李湘宁，李海宁.可靠性贝叶斯鉴定试验方案中风险确定原则［J］.战术导弹技术，2008（6）：42－44.

［8］冯文哲，刘琦.成败型产品的Bayes可靠性验证试验设计［J］.航空动力学报，2012，27（1）：110－116.

［9］周源泉，翁朝曦.可靠性评定［M］.北京：科学出版社，1990.

［10］郑锦，武翰文.Bayes序贯决策法在舰炮武器系统试验中的应用［J］.计算机与数字工程，2009（8）.

［11］刘商飞，张志祥.基于改进的Bayes判别法的中文多义词消歧［J］.计算机与数字工程，2009（10）.

［12］余华，吴文全，刘忠.Bayes理论在机器人信息融合中的应用［J］.计算机与数字工程，2009（12）.

［13］孟庆玉，周徐昌.鱼雷可靠性工程基础 ［M］.北京：科学出版社，1989.