电子天平示值误差测量结果的不确定度评定

王学琴，李承荣，滕岩 张传洪

（中国兵器工业集团第五三研究所，济南 250031） （山东省烟草专卖局，山东省烟草质量监督检测站，济南 250101）

电子天平示值误差测量结果的不确定度评定

王学琴，李承荣，滕岩 张传洪

（中国兵器工业集团第五三研究所，济南 250031） （山东省烟草专卖局，山东省烟草质量监督检测站，济南 250101）

依据JJG 1036-2008 《电子天平检定规程》，分析了电子天平示值误差测量结果不确定度的来源，以最大称量点200 g为例，对不确定度分量进行了评定与计算。当最大称量为200 g时，扩展不确定度为0.18 mg(k=2)。

电子天平；示值误差；不确定度

Wang Xueqin, Li Chengrong, Teng Yan

(CNGC Institue 53，Jinan 250031，China)

Zhang Chuanhong

(Shandong Provincial Tobacco Monoploy Bureau，Shandong Province Tobacco Quality Supervision and Test Station，Jinan 250101)

对检测／校准结果进行不确定度评定是检测／校准工作与国际接轨的需要，是ISO／IEC 17025：1999对实验室的要求。电子天平准确度高、称量速度快、显示稳定，被广泛应用于化学计量、理化检测实验室。科学、合理地评定电子天平示值误差的不确定度对于检测／校准结果具有重要意义。笔者以实验室电子天平为例，根据JJF 1059-1999［1］的要求，对电子天平示值误差测量结果进行了不确定度评定。

1 测量依据及方法

（1）测量依据：JJG 1036-2008［2］。

（2）被测对象：电子天平，最大称量200 g，分度值0.1 mg。

（3）测量标准：E2等级标准砝码200 g，JJG 99-2006［3］中给出其扩展不确定度为0.10 mg，包含因子k=2。

（4）测量方法：采用标准砝码直接测量电子天平各技术参数的示值，可得电子天平示值与标准砝码之差，即为电子天平的示值误差。

2 数学模型

电子天平的示值误差按下式计算：

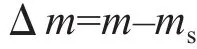
式中：Δm——电子天平示值误差；

3 不确定度评定

根据数学模型，电子天平示值误差测量结果的不确定度主要来源于两方面：标准砝码质量引入的不确定度和电子天平示值引入的不确定度。

3.1 标准砝码质量引入的标准不确定度u(ms)

u(ms)由检定证书中扩展不确定度U和覆盖因子k(通常k=2)，以及标准砝码质量的不稳定性引入的不确定度uinst(ms)计算得到，计算公式如下：

检定证书中给出200 g砝码的扩展不确定度U为0.10 mg，因此U／k＝0.10 mg／2=0.05 mg。

标准砝码质量的不稳定性引入的不确定度(由于所采用的E2等级标准砝码检定次数较少，所以只能根据年变差来计算)。由规程可知，200 g标准砝码质量的不稳定性引入的最大年变差Δ=±0.1 mg，假设服从均匀分布，包含因子则：（mg）。

因此200 g标准砝码引入的标准不确定度为：

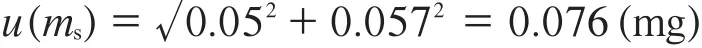
根据文献[1]估计，Δu(ms)／u(ms)=0.10，则自由度vms=50

3.2 电子天平示值引入的标准不确定度u(m)

u(m)主要来源于天平测量的重复性和天平的分辨力。

（1）测量重复性引入的标准不确定度u(m1)

用200 g标准砝码在重复性条件下对电子天平进行连续10次测量，结果见表1。

表1 重复测量结果

单次实验标准差为：

任意选取3台同类型电子天平，对每台电子天平在200 g称量点处进行3组测量，每组测量均在重复性条件下连续测量10次，共得到9组测量列，每组测量列分别按上述方法计算，得到9个单次实验标准差(sj)分别为0.052，0.071，0.082，0.068，0.072，0.090，0.077，0.063，0.086 mg。

合并样本标准偏差为：

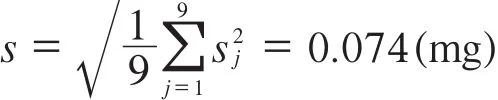
在电子天平的实际校准工作中，每次测量重复次数为6次，则：

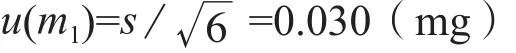
自由度：vm1=9×(10-1)=81

（2）电子天平分辨力引入的标准不确定度

该电子天平的分辨力d=0.1 mg，且服从均匀分布，则：

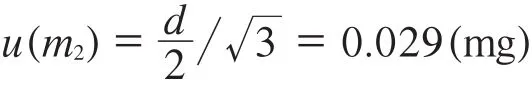
根据文献[1]估计，Δu(m2)／u(m2)=0.10，则自由度vm2=50。

（3）标准砝码的磁性引入的不确定度uF

由于标准砝码为E2等级无磁砝码，满足JJG 99-2006［3］检定规程要求，因此此项不确定度可以按照“零”计算，即uF=0。如果砝码有很高的磁化率或被磁化，则在砝码和秤盘之间放上一个无磁的盘可以减少它们之间的磁性作用。若砝码满足本检定规程的要求，则磁性引入的不确定度uF可忽略不计。

（4）偏载引入的不确定度uE

如果这项分量已知，需要对其进行评估，若有必要需把此分量加入到不确定度的评估中。

偏载引入的不确定度可按下式计算［1］：

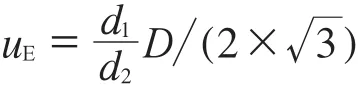
式中：d1——估计的称盘中心到砝码中心的距离；

d2——称盘中心到一个角的距离。

D——天平按照相应检定规程进行偏载测量

时最大值和最小值之间的差；

多数情况下，不确定度分量uE被检定过程中的不确定度u(m1)所覆盖，可以忽略。

因此电子天平示值引入的标准不确定度为：

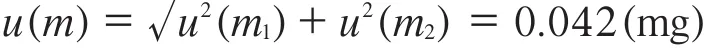
经计算：自由度vm=117。

4 合成标准不确定度计算

4.1 灵敏系数

根据数学模型，计算得灵敏系数为：

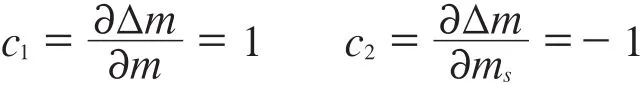
4.2 标准不确定度汇总

各输入量引入的标准不确定度列于表2。

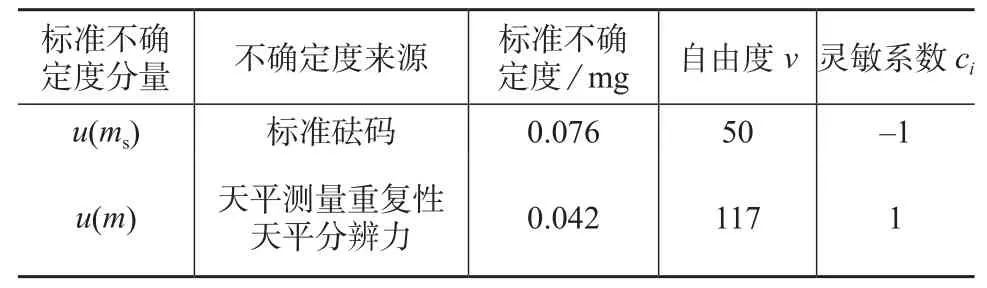
表2 不确定度汇总

4.3 合成标准不确定度

u(ms)，u(m)相互独立，互不相关，因此：

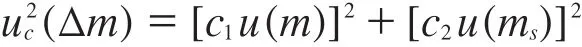
代入数据计算得：uc（Δm）＝0.087 mg

取veff=50。

5 扩展不确定度

取置信概率p=95%，按有效自由度veff=50，查t分布表得k=2，则扩展不确定度为：

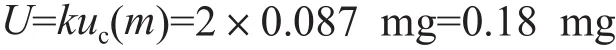
［1］ JJF1059-1999 测量不确定度评定与表示［S］.

［2］ JJG1036-2008 电子天平［S］.

［3］ JJG99-2006 砝码［S］.

Uncertainty Evaluation of the Measurement of Electronic Balance Indication Error

The sources of measurement uncertainty of electronic balance indication error were analysed according to JJG 1036-2008 Electronic Balance Verifcation Regulation. The largest weighing 200 g was taken for example, uncertainty components were calculated. The expanded uncertainty was 0.18 mg(k=2.01) as the largest weighing was 200 g.

electronic balance; indication error; uncertainty

O657.99

：A

：1008-6145(2012)04-0020-02

10.3969／j.issn.1008-6145.2012.04.006

联系人：王学琴；E-mail:wangxueqin1125@126.com

2012-04-08