核电站蒸汽发生器水位的自抗扰多模型控制方法研究

谷俊杰， 冀乃良， 孙玉洁， 谭俊龙， 王东旭

（华北电力大学 能源动力与机械工程学院，保定071003）

蒸汽发生器是压水堆核动力装置中的主要设备之一，是核电站一回路、二回路的枢纽，它的主要作用是将一回路冷却剂中的热量传递给二回路给水，使之产生蒸汽用于驱动汽轮机.当核电机组运行时，必须对蒸汽发生器水位进行监测和控制，使其处于运行限值范围内，水位过高或过低都会直接影响核电站的安全和经济运行.针对蒸汽发生器的水位控制问题，国内外科研工作者提出了多种控制方法，如鲁棒H∞控制、预测控制及模糊逻辑控制［1］.但是，蒸汽发生器的物理过程是一个非常复杂的过程，具有明显的非线性、参数时变性以及各种扰动的不确定性等特点，因此难以找到一种非常理想的控制方法.对此，笔者提出了一种新的核电站蒸汽发生器水位系统的自抗扰多模型控制方法.

1 蒸汽发生器水位的多模型控制系统结构

一般，对核电站蒸汽发生器水位的控制采用典型的三冲量（蒸汽流量、给水流量和蒸汽发生器水位）控制策略.蒸汽发生器的水位控制回路包括主给水流量调节回路和旁路给水流量调节回路［2］.由于在对蒸汽发生器水位进行实际控制的过程中，尤其在启动和低负荷运行时存在逆动力引起的收缩和膨胀效应、不同负荷运行参数不确定以及低负荷时流量传感器对扰动反应不灵敏等问题，因此传统PID控制方法难以满足核电站在不同负荷运行时机组控制品质的要求.

为了提高在负荷大范围全程变化时控制器的性能，笔者在传统PID控制器的基础上将自抗扰控制与多模型控制相结合，设计了自抗扰多模型控制器［3］，即外环控制器由多个局部自抗扰控制器（Active disturbance rejection control，ADRC）组成，每个局部ADRC是针对各个典型负荷的工况点而设计的.当控制系统运行时，各局部ADRC根据系统运行的工况给出各自的控制作用，而实际加到被控对象上的控制作用是各局部控制器输出的加权和.权重系数取决于实际对象模型与各典型工况下模型的匹配程度，其值与各模型的预测输出与实际输出的偏差有关.图1为基于ADRC的蒸汽发生器水位多模型切换控制系统结构，其中K为比例系数.

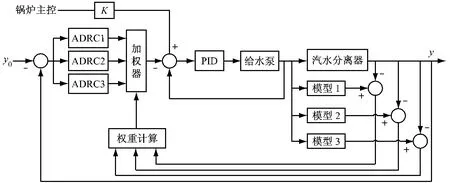
图1 基于ADRC的多模型切换控制系统结构Fig.1 Structure of a multi－model switching control system based on ADRC

2 外环局部自抗扰控制器的设计

自抗扰控制器是在反馈线性化的基础上设计的新型控制器，由跟踪微分器（TD）、扩张状态观测器（ESO）以及非线性反馈控制律（NLSEF）三部分组成.ADRC通过非线性变换将非线性系统转换成线性系统的积分串联结构，从而实现动态系统的反馈线性化.由于ADRC是根据被控系统的时间尺度划分对象的，因此设计时不用考虑系统的线性或非线性以及时变或时不变，所以比传统PID控制器具有更强的适应性和鲁棒性，同时也克服了传统PID在快速性和稳定性之间的矛盾等缺点.

目前，最常用的是二阶外环局部ADRC，其结构见图2.笔者以二阶为例，简单介绍了自抗扰控制算法［3］.

二阶不确定被控对象为：

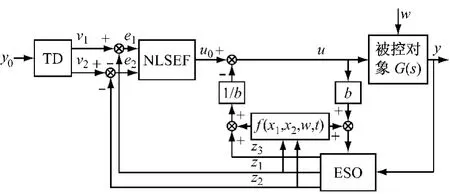
图2 外环局部ADRC控制器的结构Fig.2 Structure of a local ADRC controller in the external loop

在式（1）中，f（x1，x2，w，t）包含了系统的所有未建模动态特性（如非线性、参数时变及外扰等）.

2.1 跟踪微分器

跟踪微分器的工作原理：对给定的输入信号，经由TD后产生两路信号，一路是给定信号y0的跟踪信号v1，另一路是给定信号y0的微分信号v2.对于任意给定的连续或不连续信号y0，TD均可以给出连续、无超调的跟踪信号.跟踪的快慢取决于参数r值：r值越大，跟踪得越快；r值越小，则跟踪得越慢.

以二阶跟踪微分器为例，其微分方程为：

式中：ψ＝fst（v1，v2，r，h0），为非线性函数；h0为滤波因子；r为速度因子.

ψ的表达式为：

因此，TD不仅可以对给定信号进行预处理，安排过渡过程，还可以从不可微信号或含有噪声的信号中合理地提取出连续可微的信号.

2.2 扩张状态观测器

三阶扩张状态观测器的微分方程：

式中：u为被控对象的输入信号；y为被控对象的输出信号；β01、β02、β03为观测器系数；0＜αk≤1；fal（ε，αk，δ）（k＝1，2，3）为非线性函数，

ESO的输出信号z3是对被控对象的模型作用（内扰和外扰作用）的估计信号，只要合理地选取参数β01、β02和β03，ESO就能给出满意的估计信号，这是独立于被控对象和外扰作用的观测器.

2.3 非线性误差反馈控制律

由TD产生的跟踪信号v1和微分信号v2与ESO给出的状态估计信号z1和z2形成两个误差量：

然后选取适当的非线性函数，根据这两个误差量产生u0：

式（7）称为非线性误差反馈控制律（NLSEF），再根据ESO给出的干扰估计信号z3和被控对象的已知部分即可形成控制量u：

3 蒸汽发生器水位多模型控制的切换策略

在系统的负荷功率工作点转换时，需要对外环的局部控制器进行切换.笔者以模型输出与实际输出的匹配误差作为系统性能指标，并对控制器权值进行调整.在每个采样时刻，根据性能指标大小来调整局部模型对应的控制器权值大小［4］.

在系统运行过程中，采样时刻k时n个局部模型的预测输出为z1i（k）（i＝1，2，…，n），被控对象的实际输出为y（k），则它们之间的匹配误差为：

式中：σ为常数，0＜σ≤1.

一段时间t内的匹配误差之和为：

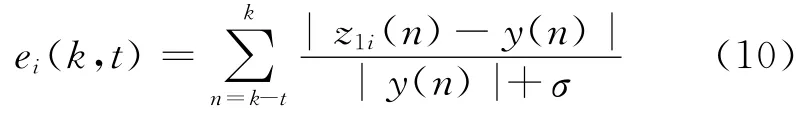
式中：t为匹配误差滚动累计长度，一般为模型的最大建模长度.

因此，可得到匹配误差的递推公式：

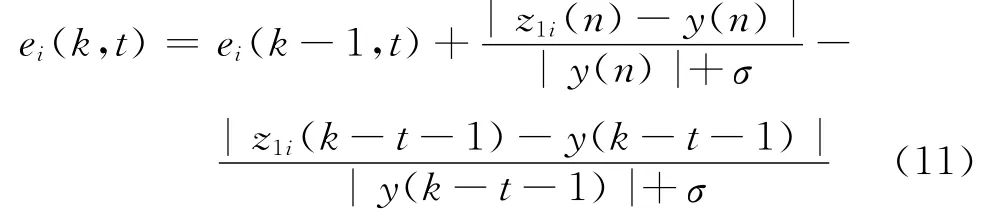
为降低历史信息的重要性，引入匹配误差的遗忘因子λ（0＜λ＜1），得到：

式中：ei为累计初值，ei（0，t）＝0.

外环主控制器输出采用外环各局部控制器加权和的形式，而各局部控制器输出权重的计算方法为：

Narendra K S等已证明了不同的切换方案不影响系统稳定性，只要每个控制器单独使用，系统是全局稳定的.因此，为保证上述切换算法的稳定，只需确保每个对象模型与其相应的控制器组成的闭环系统稳定.

4 核电站蒸汽发生器水位系统的仿真

4.1 蒸汽发生器动态数学模型的机理分析

以核电站立式U型管蒸汽发生器（额定参数见文献［5］）为例，在描述蒸汽发生器模型主要动力的同时，应该是简单和相对准确的.Irving等［5］给出的线性变参数模型已被广泛应用到蒸汽发生器水位的控制中，水位Y的传递函数与水流量Qe和蒸汽流量Qv有关，传递函数为

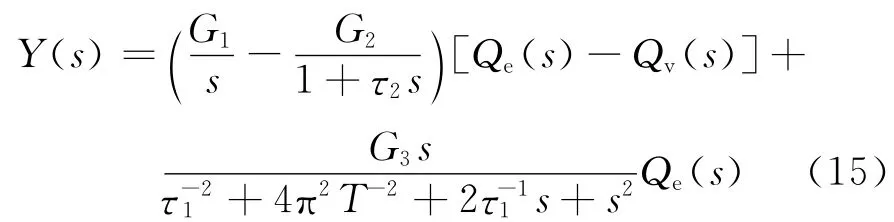
式中：G1／s为蒸汽发生器大容量的影响，计算蒸汽流量变化而引起的水位的改变量；－G2／（1＋τ2s）为热效应引起的膨胀和收缩现象的影响，初始时由给水和蒸汽流量改变引起；为给水流动引起的机械振动的影响.

表1为不同负荷下蒸汽发生器模型参数的变化量［6］.若给水流量和蒸汽流量分别用μ和d表示，则式（15）可表示为：

因此，在对蒸汽发生器水位进行控制时，可以将给水流量和蒸汽流量作为扰动进行控制器的仿真模拟［7］.

表1 不同负荷下蒸汽发生器模型参数的变化量Tab.1 Variation of steam generator model parameters at different loads

4.2 控制系统的仿真与结果分析

在仿真过程中，应用Matlab中的Simulink建立系统模型，自抗扰控制器可应用其中的工具箱进行编辑，运用自抗扰算法实现适当的参数设置，并对提出的算法采用S函数编程.在不同功率点，对蒸汽发生器水位进行仿真，并在50s和400s时分别加入给水扰动和蒸汽流量扰动，同时与传统PID控制器进行比较.图3为不同负荷下给水扰动和蒸汽扰动时蒸汽发生器水位的仿真曲线.从图3可知：自抗扰控制器对蒸汽发生器水位具有良好的控制效果，并对控制系统的不确定性和外部扰动变化具有较强的适应性和鲁棒性，其利用的非线性结构从根本上克服了传统PID控制固有的缺陷，能有效解决控制对象的模型不确定性、多扰动及时滞等问题［8］.从图3的仿真曲线可以看出：在不同负荷下，当出现负荷变化时，自抗扰控制器能够快速作出反应，将输出控制在理想的范围内，达到了改善系统控制效果的目的.

图3 不同负荷下给水扰动和蒸汽扰动时蒸汽发生器水位的仿真曲线Fig.3 Simulation curves of steam generator water level with feedwater and steam flow disturbance at different loads

5 结 论

（1）自抗扰控制器由扩展状态观测器实时估计出系统扰动，并通过扰动补偿有效消除其影响，再应用反馈控制率进行控制且不需要精确模型，具有超调小、响应快以及抗干扰能力强等特点.

（2）在采用自抗扰控制的同时，与多模型控制相结合并应用于核电站蒸汽发生器水位的控制系统中，利用ESO实时估计出各种干扰，并通过扰动的前馈补偿有效提高蒸汽发生器水位控制的抗干扰和自适应能力，为核电站蒸汽发生器水位的控制提供了一种新的方案.

［1］MUNASINGHE S R，KIM M S，LEE J J.Adaptive neurofuzzy controller to regulate UTSG water level in nuclear power plants［J］.IEEE Trans Nucl Sci，2005，52（1）：421－429.

［2］陈智，张英，张帆，等.岭澳核电站蒸发器水位控制系统改进方案仿真研究［J］.核动力工程，2010，31（4）：66－70.CHEN Zhi，ZHANG Ying，ZHANG Fan，et al.Simulation study on improvement of steam generator level control system of Ling’ao Nuclear Power Station［J］.Nuclear Power Engineering，2010，31（4）：66－70.

［3］韩京清.自抗扰控制技术——估计补偿不确定因素的控制技术［M］.北京：国防工业出版社，2009：5.

［4］张智焕，王树青.基于多模型切换的大范围预测函数控制 ［J］.浙江大学学报，2002，36（3）：291－293.ZHANG Zhihuan，WANG Shuqing.Global predictive function control based on the switching of multiple models［J］.Journal of Zhejiang University，2002，36（3）：291－293.

［5］IRVING E，MIOSSEC C，TASSART J.Towards efficient full automatic operation of the PWR steam generator with water level adaptive control［C］／／Proceedings of the 2nd International Conference on Boiler Dynamics and Control in Nuclear Power Stations.London，England：［s.n.］，1980.

［6］HU Ke，YUAN Jingqi.Multi－model predictive control method for nuclear steam generator water level［J］.Energy Conversion and Management，2008，49（5）：1167－1174.

［7］谷俊杰，米克嵩，徐培培.基于遗传算法的核电站蒸汽发生器高阶水位模型的降阶方法［J］.动力工程学报，2010，30（2）：115－117.GU Junjie，MI Kesong，XU Peipei.Order reduction method of the high order nuclear steam generator level control model based on genetic algorithm［J］.Journal of Chinese Society of Power Engineering，2010，30（2）：115－117.

［8］ZHENG Qing，CHEN Zhongzhou，GAO Zhiqiang.A practical approach to disturbance decoupling control［J］.Control Engineering Practice，2009，17（9）：1016－1025.